October | 2009 | Tangled Web

Archive for October, 2009

Ribbon categories

October 23, 2009

In the last post I discussed the category of framed oriented tangles, which according to Shum’s theorem is a free ribbon category. As a corollary to Shum’s theorem, we may derive tangle invariants from any ribbon category. Let’s see how this works for the Kauffman bracket.

Consider planar diagrams, that is curves in the plane. These are like tangle diagrams only without self-intersections, i.e. no crossings. Just like tangles, they form a monoidal category since we can place them side by side or atop each other. Also just like tangles they have duality cups and caps.

Cup and Cap

Inspired by the definition of the Kauffman bracket, we extend the category of planar diagrams by linear combinations with coefficients polynomials in $A,A^{-1}$ and mod out by the circle relation:

Circle Relation

This gives a braiding and twist as in the calculations for the Kauffman bracket.

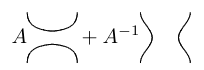
Braiding

Twist

The resulting ribbon category is called the Temperley-Lieb category, named for mathematicians who studied its implications in the context of statistical mechanics.

Now we have two examples of ribbon categories, the category of tangles and the Temperley-Lieb category. How else can we generate examples of ribbon categories? Recall that the category of finite dimensional vector spaces and linear maps formed a monoidal category with duals. We consider the subcategory of representations of an algebra $A$ .

An algebra is a vector space in which we have a multiplication and unit with the familiar properties of associativity and unitality. For example, given a vector space $V$ the space $End(V)$ of endomorphisms of $V$ , that is linear maps $V\to V$ , forms an algebra where our multiplication is composition of linear maps and our unit is the identity map $1_V$ . $V$ is a representation of $A$ iff there is a linear map $\rho_V:A\to End(V)$ which preserves multiplication and unit.

A Hopf algebra, in addition to having a multiplication and unit, also has maps $\Delta:A\to A\otimes A, \eta:A\to k$ called comultiplication, counit which are coassociative, and counital where $k$ is the field of scalars. This guarantees that the category $Rep_{fd}(A)$ of finite dimensional representations of $A$ is monoidal since we can define representations $\rho_{V\otimes W}=(\rho_V\otimes \rho_W)\Delta$ and $\rho_k=\eta$ . We also require a map $S:A\to A$ called the antipode which switches the order of multiplication and is the convolution inverse to the identity. This guarantees that $Rep_{fd}(A)$ has left duals with $\rho_{V^*}=\rho_V S$ .

If there are elements $R\in A\otimes A,h\in A$ such that $P_{V,W}(\rho_V\otimes\rho_W)(R)$ is a braiding, where $P_{V,W}:V\otimes W\to W\otimes V$ is the swap map $P_{V,W}(v\otimes w)=w\otimes v$ and where $\rho_V(h)$ is a twist, then we call $A$ a ribbon Hopf algebra. Clearly then $Rep_{fd}(A)$ is a ribbon category.

Surprisingly, ribbon Hopf algebras turn up in the study of Lie algebras. One may “quantize” a Lie algebra, deforming it by a formal parameter meant to mimic Plank’s constant $\hbar$ and the result is a ribbon Hopf algebra. This discovery led to a whole slew of new invariants and a new understanding of old invariants. For instance the Jones’ polynomial and the Kauffman bracket are related to the quantization of the most basic Lie algebra $sl(2,\mathbb{C})=su(2)\otimes\mathbb{C}=so(3)\otimes\mathbb{C}$ . Invariants of tangles derived from quantized Lie algebras are called Reshetikhin-Turaev invariants or simply quantum invariants. When applied to links they give polynomials in a variable $q=e^\hbar$ .

Posted in Topology | 5 Comments »

The category of tangles

October 1, 2009

I want to get back to discussing tangles. So far we’ve been thinking about tangles entirely topologically. But as it turns out, tangles are also fundamentally algebraic objects. The algebraic gadget we need to understand tangles is that of a free ribbon category. Indeed, Shum’s theorem states that framed, oriented tangles form the morphisms of a free ribbon category on a single generator.

To begin to understand this deep statement we must start with the definition of a category. A category is a set of objects $A,B,C,\ldots$ along with a class (for technical reasons a class, not a set) of morphisms $f,g,h,\ldots$ . Each morphism has a source object and a target object so that we can think of a morphism as an arrow $B\leftarrow A$ . There is a composition operation of morphisms $gf$ which is defined only if the source of $g$ is the target of $f$ . There is also an identity morphism $1_A$ for every object $A$ whose source and target are both $A$ . Finally we require that composition be associative $(hg)f=h(gf)$ and unital $1_B f=f=f 1_A$ .

Tangles form morphisms in a category. Just let the objects be points in a plane; then clearly tangles form morphisms with their bottom endpoints as source and their top endpoints as target (or vice versa, it’s just a convention). We can compose tangles by placing them one atop the other, so long as their sources and targets match up. Identity tangles are simply a bunch of vertical lines connecting matching top and bottom endpoints. Clearly, associativity and unitality hold so tangles do indeed form a category.

We can form a category of tangles with a completely different composition however. Instead of placing tangles atop each other, we can place them side by side. Now the empty tangle is the identity. Also, in this category there is only 1 object since we can always place tangles next to each other; there’s nothing to match up! Something with 2 different categorical structures like this is called, logically enough, a 2-category. But, as we said, the second category structure has a unique object. These kinds of 2-categories are so common they get their own name, monoidal categories. Thus, tangles form the morphisms of a monoidal category.

Actually, that’s not the end of the story! We could put the tangles side by side in different ways, since the endpoints live in planes, we have 2 dimensions to work with. The two independent ways of placing tangles next to each other in addition to the standard composition of placing them atop each other turn tangles into a 3-category. Since both ways of putting tangles next to each other can be done without worrying about matching this is a special kind of 3-category called a doubly monoidal category. Doubly monoidal categories always have a way of transforming the monoidal product (side-by-side placement) into its opposite (side-by side placement but in the reverse order). This comes from the fact that the 2 monoidal structures are essentially the same. Try to think about why this is true for tangles.

Let’s think about how to transform two points sitting side by side into the same two points sitting in the opposite order. As we transform in two dimensions rotating one around the other, we trace out the familiar crossing. Of course we can rotate them in the other direction and get the other crossing.

Crossings

In general, this sort of thing is called a braiding, and doubly monoidal categories always have them. For this reason, they’re also called braided monoidal categories.

Orientation means that the endpoints of our tangle are more than just points. They have directions associated with them, either up or down. We call this a dual structure, since the dual of up is down. This is familiar from linear algebra where to each vector space $V$ we can associate a dual vector space $V^*$ of linear maps from $V$ to the field of scalars. The important structure relating vector spaces and their duals are the evaluation and coevalutation maps. Evaluation takes a dual vector $f$ and a vector $v$ and evaluates to the scalar $f(v)$ . Coevaluation makes use of the isomorphism $V\otimes V^*=End(V)$ where $End(V)$ is the space of endomorphisms of $V$ . The coevaluation takes a scalar to that scalar multiple of the identity. Now, we have the same sort of structure morphisms in the category of tangles, the caps and cups. This makes the category of tangles a monoidal category with duals, just like the category of linear transformations of vector spaces.

Cap and Cup

Since cups and caps may be oriented in 2 different ways, we have 2 dual structures, a left and a right dual. The same can be said of the category of vector spaces but there, one simply identifies left and right duals. In the category of tangles it’s not so easy. Instead one must build a natural isomorphism between left and right duals and for this you need a twist. A twist is what it sounds like, take your endpoints and twist them around 360 degrees. This is where framing comes into play. If you do this to a single endpoint, you get a ribbon with a full twist in it. This has a blackboard diagram that looks like either side of the framed Reidemeister 1 move.

Twist on 1 strand

What if you had 2 endpoints? Think about this for a bit, you get 2 crossings between 2 ribbons each of which has a full twist in it. Luckily this is the compatibility condition between the braiding and the twist that is required of a so-called ribbon category.

Twist on 2 strands

To recap, a ribbon category is a braided monoidal category with duals and a twist. All of these may be defined algebraically but have intuitive topological definitions in the category of tangles. The fact that algebra may be thought about topologically can be rigorously summed up in the statement of Shum’s theorem given at the beginning of the post: framed, oriented tangles form the morphisms of a free ribbon category on a single generator.

Posted in Math, Topology | 4 Comments »

Tangled Web

Archive for October, 2009

Ribbon categories

The category of tangles

Archives

Categories