Introduction to Height Balanced Binary Tree
Last Updated :
03 Apr, 2023
A height-balanced binary tree is defined as a binary tree in which the height of the left and the right subtree of any node differ by not more than 1. AVL tree, red-black tree are examples of height-balanced trees.
 Height Balanced tree
Height Balanced treeConditions for Height-Balanced Binary Tree:
Following are the conditions for a height-balanced binary tree:
- The difference between the heights of the left and the right subtree for any node is not more than one.
- The left subtree is balanced.
- The right subtree is balanced.
Note: An empty tree is also height-balanced.
What is the Height Balance of a node?
To check if the binary tree is height-balanced or not, you have to check the height balance of each node. For this, you need to calculate the heights of the two subtrees for each node making this impractical. Instead, we store the height balance information of every subtree in the root node of that subtree. Thus, each node not only maintains its data and children's information but also a height balance value.
The height balance of a node is calculated as follows:
height balance of node = height of right subtree - height of left subtree
The above formula means that:
- If the right subtree is taller, the height balance of the node will be positive.
- If the left subtree is taller, the balance of the node will be negative.
 Height-balanced and Unbalanced binary tree
Height-balanced and Unbalanced binary treeHeight of a Height-Balanced Binary Tree:
The height of a node in a tree is the length of the longest path from that node downward to a leaf, counting both the start and end vertices of the path. The height of a leaf is 1. The height of a nonempty tree is the height of its root. It can be proved that the height of a height-balanced binary tree with N nodes is O(logN).
Proof:
The minimum number of nodes in a height-balanced binary tree of height h is greater than 2h/2-1 nodes and let this is denoted by the function f(h), i.e. f(h) > 2h/2-1
This can be proved using mathematical induction.
- A height-balanced binary tree of height 1 has at least 2 node. So f(1) = 2 > 21/2 - 1 .
- A height-balanced binary tree of height 2 has a minimum of 4 nodes i.e., the root node, its two children and at least one node at depth of 2. So f(2) = 4 > 22/2 - 1.
- Now consider the statement is true for some value of height (h-1) > 2. So we have to prove that it is also valid for height = h.
A tree of height h, has a root and its two subtrees. One of the subtrees will have height h-2 and the other h-1 (because we want the minimum number of nodes). So,
f(h) = 1 + f(h-1) + f(h-2)
f(h) > 1 + 2 * f(h-2) because f(h-1) > f(h-2)
f(h) > 2 * f(h-2).
As the statement is true for values less than h,
So f(h) > 2*2(h-2)/2 - 1
i.e., f(h) > 2h/2-1. - So we can see
log( f(h) ) > h/2 - 1 or
h/2 < log( f(h) ) + 1
h < 2*log( f(h) ) + 2
h < 2*log(N) + 2 [say the minimum number of nodes is N. So f(h) = N]
Therefore it is proved that h = O(logN)
Why do we need a Height-Balanced Binary Tree?
Let's understand the need for a balanced binary tree through an example.
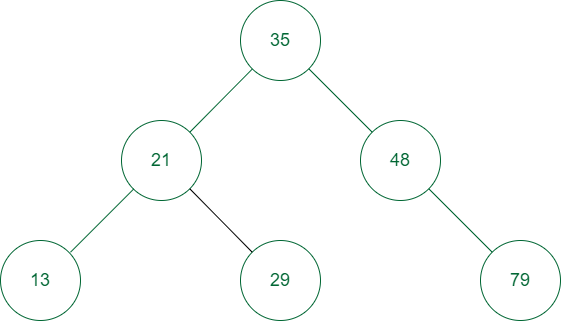 Binary search tree
Binary search tree
The above tree is a binary search tree and also a height-balanced tree.
Suppose we want to find the value 79 in the above tree. First, we compare the value of the root node. Since the value of 79 is greater than 35, we move to its right child, i.e., 48. Since the value 79 is greater than 48, so we move to the right child of 48. The value of the right child of node 48 is 79. The number of hops required to search the element 79 is 2.
Similarly, any element can be found with at most 2 jumps because the height of the tree is 2.
So it can be seen that any value in a balanced binary tree can be searched in O(logN) time where N is the number of nodes in the tree. But if the tree is not height-balanced then in the worst case, a search operation can take O(N) time.
Applications of Height-Balanced Binary Tree:
- Balanced trees are mostly used for in-memory sorts of sets and dictionaries.
- Balanced trees are also used extensively in database applications in which insertions and deletions are fewer but there are frequent lookups for data required.
- It is used in applications that require improved searching apart from database applications.
- It has applications in storyline games as well.
- It is used mainly in corporate sectors where they have to keep the information about the employees working there and their change in shifts.
Advantages of Height-Balanced Binary Tree:
- It will improve the worst-case lookup time at the expense of making a typical case roughly one lookup less.
- As a general rule, a height-balanced tree would work better when the request frequencies across the data set are more evenly spread,
- It gives better search time complexity.
Disadvantages of Height-Balanced Binary Tree:
- Longer running times for the insert and remove operations.
- Must keep balancing info in each node.
- To find nodes to balance, must go back up in the tree.
How to check if a given tree is height-balanced:
You can check if a tree is height-balanced using recursion based on the idea that every subtree of the tree will also be height-balanced. To check if a tree is height-balanced perform the following operations:
- Use recursion and visit the left subtree and right subtree of each node:
- Check the height of the left subtree and right subtree.
- If the absolute difference between their heights is at most 1 then that node is height-balanced.
- Otherwise, that node and the whole tree is not balanced.
Refer to our article on "How to determine if a binary tree is height-balanced" for implementation of this.
Similar Reads
Introduction to Tree Data Structure Tree data structure is a hierarchical structure that is used to represent and organize data in the form of parent child relationship. The following are some real world situations which are naturally a tree.Folder structure in an operating system.Tag structure in an HTML (root tag the as html tag) or
15+ min read
Tree Traversal Techniques Tree Traversal techniques include various ways to visit all the nodes of the tree. Unlike linear data structures (Array, Linked List, Queues, Stacks, etc) which have only one logical way to traverse them, trees can be traversed in different ways. In this article, we will discuss all the tree travers
7 min read
Applications of tree data structure A tree is a type of data structure that represents a hierarchical relationship between data elements, called nodes. The top node in the tree is called the root, and the elements below the root are called child nodes. Each child node may have one or more child nodes of its own, forming a branching st
4 min read
Advantages and Disadvantages of Tree Tree is a non-linear data structure. It consists of nodes and edges. A tree represents data in a hierarchical organization. It is a special type of connected graph without any cycle or circuit.Advantages of Tree:Efficient searching: Trees are particularly efficient for searching and retrieving data.
2 min read
Difference between an array and a tree Array:An array is a collection of homogeneous(same type) data items stored in contiguous memory locations. For example, if an array is of type “intâ€, it can only store integer elements and cannot allow the elements of other types such as double, float, char, etc. The array is a linear data structure
3 min read
Inorder Tree Traversal without Recursion Given a binary tree, the task is to perform in-order traversal of the tree without using recursion.Example:Input:Output: 4 2 5 1 3Explanation: Inorder traversal (Left->Root->Right) of the tree is 4 2 5 1 3Input:Output: 1 7 10 8 6 10 5 6Explanation: Inorder traversal (Left->Root->Right) o
8 min read
Types of Trees in Data Structures A tree in data structures is a hierarchical data structure that consists of nodes connected by edges. It is used to represent relationships between elements, where each node holds data and is connected to other nodes in a parent-child relationship.Types of Trees TreeThe main types of trees in data s
4 min read
Generic Trees (N-ary Tree)
Introduction to Generic Trees (N-ary Trees)Generic trees are a collection of nodes where each node is a data structure that consists of records and a list of references to its children(duplicate references are not allowed). Unlike the linked list, each node stores the address of multiple nodes. Every node stores address of its children and t
5 min read
Inorder traversal of an N-ary TreeGiven an N-ary tree containing, the task is to print the inorder traversal of the tree. Examples:Â Input: N = 3Â Â Output: 5 6 2 7 3 1 4Input: N = 3Â Â Output: 2 3 5 1 4 6Â Approach: The inorder traversal of an N-ary tree is defined as visiting all the children except the last then the root and finall
6 min read
Preorder Traversal of an N-ary TreeGiven an N-ary Tree. The task is to write a program to perform the preorder traversal of the given n-ary tree. Examples: Input: 3-Array Tree 1 / | \ / | \ 2 3 4 / \ / | \ 5 6 7 8 9 / / | \ 10 11 12 13 Output: 1 2 5 10 6 11 12 13 3 4 7 8 9 Input: 3-Array Tree 1 / | \ / | \ 2 3 4 / \ / | \ 5 6 7 8 9 O
14 min read
Iterative Postorder Traversal of N-ary TreeGiven an N-ary tree, the task is to find the post-order traversal of the given tree iteratively.Examples: Input: 1 / | \ 3 2 4 / \ 5 6 Output: [5, 6, 3, 2, 4, 1] Input: 1 / \ 2 3 Output: [2, 3, 1] Approach:We have already discussed iterative post-order traversal of binary tree using one stack. We wi
10 min read
Level Order Traversal of N-ary TreeGiven an N-ary Tree. The task is to print the level order traversal of the tree where each level will be in a new line. Examples: Input: Image Output: 13 2 45 6Explanation: At level 1: only 1 is present.At level 2: 3, 2, 4 is presentAt level 3: 5, 6 is present Input: Image Output: 12 3 4 56 7 8 9 10
11 min read
ZigZag Level Order Traversal of an N-ary TreeGiven a Generic Tree consisting of n nodes, the task is to find the ZigZag Level Order Traversal of the given tree.Note: A generic tree is a tree where each node can have zero or more children nodes. Unlike a binary tree, which has at most two children per node (left and right), a generic tree allow
8 min read
Binary Tree
Introduction to Binary TreeBinary Tree is a non-linear and hierarchical data structure where each node has at most two children referred to as the left child and the right child. The topmost node in a binary tree is called the root, and the bottom-most nodes are called leaves. Introduction to Binary TreeRepresentation of Bina
15+ min read
Properties of Binary TreeThis post explores the fundamental properties of a binary tree, covering its structure, characteristics, and key relationships between nodes, edges, height, and levelsBinary tree representationNote: Height of root node is considered as 0. Properties of Binary Trees1. Maximum Nodes at Level 'l'A bina
4 min read
Applications, Advantages and Disadvantages of Binary TreeA binary tree is a tree that has at most two children for any of its nodes. There are several types of binary trees. To learn more about them please refer to the article on "Types of binary tree" Applications:General ApplicationsDOM in HTML: Binary trees help manage the hierarchical structure of web
2 min read
Binary Tree (Array implementation)Given an array that represents a tree in such a way that array indexes are values in tree nodes and array values give the parent node of that particular index (or node). The value of the root node index would always be -1 as there is no parent for root. Construct the standard linked representation o
6 min read
Complete Binary TreeWe know a tree is a non-linear data structure. It has no limitation on the number of children. A binary tree has a limitation as any node of the tree has at most two children: a left and a right child. What is a Complete Binary Tree?A complete binary tree is a special type of binary tree where all t
7 min read
Perfect Binary TreeWhat is a Perfect Binary Tree? A perfect binary tree is a special type of binary tree in which all the leaf nodes are at the same depth, and all non-leaf nodes have two children. In simple terms, this means that all leaf nodes are at the maximum depth of the tree, and the tree is completely filled w
4 min read
Ternary Tree