RStanとShinyStanによるベイズ統計モデリング入門
71 likes37,487 views
第50回 TokyoR 発表資料 Stanコードは下のサイトで公開しております。 https://github.com/teuder/TokyoR50
![R で Stan
[ efS +bSU]SY e%U%sdefS t) seZ[ kefS
&&
RStan
RからStanを利用するインターフェース
インストール
ShinyStan
RStanの推定結果をいい感じに表示してくれる
（形式を合わせれば Stan 以外の MCMC ツールの結果も取り込める）
RStan Getting Started をみながらゴニョゴニョした後](https://image.slidesharecdn.com/tokyor50-150904231218-lva1-app6891/85/RStan-ShinyStan-21-320.jpg)
![階層ベイズモデル
y
a b[1]
s
普通のベイズ統計モデル 階層ベイズモデル
パラメターに対して、ハイパーパラメターを使って
（経験に基づいた）情報的な事前分布を設定する。
→パラメターに制約を課すことで推定が可能になる。
b[K]…
y
a b[1] b[K]…
無情報 無情報 無情報 無情報
無情報
パラメタ数が多すぎると推定できない….
パラメター
観測値
ハイパー
パラメター](https://image.slidesharecdn.com/tokyor50-150904231218-lva1-app6891/85/RStan-ShinyStan-48-320.jpg)
![階層ベイズモデル
r
bSdS_RZ[ d 9* jfdSUf%X[fRZ[ d&
k+aTe 9* Z[ef%k) Td S]e:e c%-).--)Tk:.-&&
k+bdV 9* Z[ef%Ua E S e%bSdS_RZ[ d"kRZSf&)
Td S]e:e c%-).--)Tk:.-&&
b af%k+aTe"_[Ve) k+aTe"Uag fe) Ua :
T SU]
) bUZ:.6
) j ST:
) k ST:
&
ba[ fe%k+bdV"_[Ve) k+bdV"Uag fe) Ua :
d V
) bUZ:.6&
l
l+aTe 9* Z[ef%l) Td S]e:e c%*.2).2)Tk:/&&
l+bdV 9* Z[ef%Ua E S e%bSdS_RZ[ d"l&) Td S]e:e c%*.2).2)Tk:/&&
b af% l+aTe"_[Ve) l+aTe"Uag fe) Ua :
T SU]
) bUZ:.6
) j ST:
l
) k ST:
&
ba[ fe%l+bdV"_[Ve) l+bdV"Uag fe) Ua :
d V
) bUZ:.6&
テストの点数の分布へのあてはめ、各生徒の解答力の推定](https://image.slidesharecdn.com/tokyor50-150904231218-lva1-app6891/85/RStan-ShinyStan-58-320.jpg)
More Related Content
What's hot (20)
Similar to RStanとShinyStanによるベイズ統計モデリング入門 (20)
RStanとShinyStanによるベイズ統計モデリング入門
- 2. アウトライン 統計モデルとは ベイズ推定 MCMC法 Stanの概要 R で Stan 統計モデルのデータへのあてはめ ShinyStanで結果の可視化 Stan文法 線形回帰モデル 階層ベイズモデル
- 4. ベイズ統計モデリング？ ベイズ統計 統計モデル y ∼ f (x,θ)
- 5. ベイズ統計モデリング？ ベイズ統計 統計モデル y ∼ f (x,θ)f (θ | y) ∝ f (y |θ) f (θ)
- 6. 統計モデル 関心のある観測値 y を生成する確率分布 f を 別の観測値 x や未知の値 θ を含む数式で近似したもの 現実によくフィットした統計モデルの発見は →将来発生する y の値の予測、観測できない量の推定 →現実の背景にある構造・法則性への理解につながる 定数・説明変数 パラメター 目的変数 統計 モデル p = f (y | x,θ) y p 面積1
- 7. 統計モデル 関心のある観測値 y を生成する確率分布 f を 別の観測値 x や未知の値 θ を含む数式で近似したもの 現実によくフィットした統計モデルの発見は →将来発生する y の値の予測、観測できない量の推定 →現実の背景にある構造・法則性への理解につながる 定数・説明変数 パラメター 目的変数 統計 モデル p = f (y | x,θ) y p ご注意 この発表では、あらゆる確率（密度）分布の関数を 同じ記号 f で表記する 面積1
- 8. 統計モデル 関心のある観測値 y を生成する確率分布 f を 別の観測値 x や未知の値 θ を含む数式で近似したもの 現実によくフィットした統計モデルの発見は →将来発生する y の値の予測、観測できない量の推定 →現実の背景にある構造・法則性への理解につながる 定数・説明変数 パラメター 目的変数 統計 モデル p = f (y | x,θ) y p ご注意 この発表では、あらゆる確率（密度）分布の関数を 同じ記号 f で表記する y ∼ f (x,θ) 面積1
- 9. 統計モデル p = f (y |θ) ↓ θ がある値の時に観測値 y が得られる確率 p (注1) 尤度が計算できる （注1）全ての観測値 y = {y1,...,yN} が同時に得られる確率
- 10. 統計モデル p = f (y |θ) ↓ θ がある値の時に観測値 y が得られる確率 p (注1) 尤度が計算できる （注1）全ての観測値 y = {y1,...,yN} が同時に得られる確率 尤度が大きくなるθの値からは 観測値と同じデータが得られやすいので 尤（もっと）もらしい値である y を定数として尤度を θ の関数とみなしたもの 尤度関数 L(θ) =
- 11. 統計モデルを観測値にあてはめる 最尤推定 ベイズ推定 ↓ 観測値 y が生成されやすいθの値を求める Stanはどちらにも対応している 尤度を最大化する θの値を求める 尤度と事前分布から θの事後確率分布を求める 正しいθの値は1つ あるθ値が正しい確率
- 12. f(θ|y) ∝ f(θ)f(y|θ) ベイズ推定 θの 事後分布 θの 事前分布 θの 尤度比例 データに基づいた θの確率分布 データに基づいた θの重み 前知識に基づいた θの確率分布 x←
- 13. f(θ|y) ∝ f(θ)L(θ) ベイズ推定 θの 事後分布 θの 事前分布 θの 尤度比例 データに基づいた θの確率分布 データに基づいた θの重み 前知識に基づいた θの確率分布 x←
- 18. ベイズ推定 尤度と事前分布の関数があれば 事後分布の核となる関数が得られる f(θ|y) ∝ f(θ)L(θ) θの 事後分布 θの 事前分布 θの 尤度 分布の点の値はすぐに得られるが その全体的な形はわからない場合が多い マルコフ連鎖モンテカルロ法 Markov Chain Monte Carlo methods; MCMC 任意の分布関数の形をあぶりだすアルゴリズム 比例
- 20. Stan Stan 記法により ユーザーが独自の統計モデルを記述できる が 実数のパラメターしか推定できない とはいえ離散パラメターを含むモデルも 工夫（周辺化）すれば推定できないわけではない（らしい） MCMCアルゴリズムとしてHMC(1), NUTS(2)を実装 目的の分布に素早く収束しやすい (1) ハミルトニアン・モンテカルロ法 (2) No-U-Tern Sampler
- 21. R で Stan [ efS +bSU]SY e%U%sdefS t) seZ[ kefS && RStan RからStanを利用するインターフェース インストール ShinyStan RStanの推定結果をいい感じに表示してくれる （形式を合わせれば Stan 以外の MCMC ツールの結果も取り込める） RStan Getting Started をみながらゴニョゴニョした後
- 22. 基本的なフロー Stanコード ↓ C++でコンパイル ↓ 推定実行 ↓ 収束診断 ↓ 推定結果 s_aV +efS t Sg UZReZ[ kefS %X[f& X[f 9* efS %s_aV +efS t&
- 23. 基本的なフロー Stanコード ↓ C++でコンパイル ↓ 推定実行 ↓ 収束診断 ↓ 推定結果 s_aV +efS t Sg UZReZ[ kefS %X[f& _aV 9* efS R_aV %s_aV +efS t& X[f 9* eS_b [ Y%_aV & ベイズ推定 abf[_[l[ Y%_aV & 最尤推定
- 24. 基本的なフロー Stanコード ↓ C++でコンパイル ↓ 推定実行 ↓ 収束診断 ↓ 推定結果 s_aV +efS t Sg UZReZ[ kefS %X[f& _aV 9* efS R_aV %s_aV +efS t& X[f 9* eS_b [ Y%_aV & ベイズ推定 abf[_[l[ Y%_aV & 最尤推定 defS Rabf[a e%SgfaRid[f : K & abf[a e%_U+Uad e : bSdS 77V f Uf>ad e%&&推定の並列化
- 25. はじめてのベイズ推定
- 26. 正規分布の平均と標準偏差の推定 #日本の成人男性1000人分の身長データ (cm)をシミュレーション F 9* .--- k 9* d ad_% F) _ S : .4/) eV : 2+2& 身長cm 人数
- 27. VSfS m ,,IfS r [ f9 ai d:.; F8 ,, Fu、 rv d S kPF 8 ,, r k u F v n bSdS_ f de m ,, r d S _g8 ,, u rv d S 9 ai d:-; e[Y_S8 ,, “ u rp- v n _aV m ,, _g o ad_S % -) .---&8 ,, _g u v e[Y_S o ad_S % -) .---&8 ,,e[Y_S u v k o ad_S %_g) e[Y_S&8 ,, k u v n 正規分布の平均と標準偏差の推定 Stan ※Stanでは事前分布を指定しないと一様分布が指定される。
- 28. F 9* .--- k 9* d ad_% F) _ S : .4/) eV : 2+2& efS r ad_S RVSfS 9* [ef%F : F) k : k& r x X[fR ad_S 9* ,,efS X[f efS % X[ : ad_S +efS ,,efS ) VSfS : ad_S RVSfS ,, r ) [f d : /--- ,, r ) UZS[ e : 1 ,, ) fZ[ : . ,,fZ[ :/ . {~ ) iSd_ : X aad%[f d,/&& ,,iSd_*gb MCMCサンプル数 = (iter - warm)*chain*(1/thin) = 4000 正規分布の平均と標準偏差の推定 R
- 31. #パラメターの推定値の表示 print(fit_normal) B X d U Xad IfS _aV 7 ad_S + 1 UZS[ e) SUZ i[fZ [f d:/---8 iSd_gb:.---8 fZ[ :.8 baef*iSd_gb VdSie b d UZS[ :.---) fafS baef*iSd_gb VdSie:1---+ _ S e R_ S eV /+2# /2# 2-# 42# 64+2# R XX ZSf _g .4/+06 -+-- -+.4 .4/+-2 .4/+/5 .4/+06 .4/+2. .4/+40 /163 . e[Y_S 2+11 -+-- -+./ 2+/. 2+02 2+11 2+2/ 2+34 /004 . bRR */.6-+-0 -+-0 .+-2 */.6/+5/ */.6-+06 */.56+4- */.56+0- */.56+-2 ..6- . IS_b e i d VdSi ge[ Y FK I%V[SYR & Sf Ea <gY 0. .27-27-. /-.2+ Aad SUZ bSdS_ f d) R XX [e S UdgV _ Segd aX XX Uf[h eS_b e[l ) S V ZSf [e fZ baf f[S eUS d VgUf[a XSUfad a eb [f UZS[ e %Sf Ua h dY U ) ZSf:.&+ MCMCサンプルの 平均、平均の標準誤差、標準偏差、x%値、有効サンプル数、 ˆR 正規分布の平均と標準偏差の推定
- 32. 正規分布の平均と標準偏差の推定 jfdSUf% aT Uf : FKDD efS X[f ) bSde : FKDD y r ) b d_gf V : A<DI r ） ) [ URiSd_gb : A<DI & iSd_*gb #サンプルされたパラメター値の抽出 bSdS_R ad_S 9* jfdSUf%X[fR ad_S & _g _ S % bSdS_R ad_S "_g & .4/+0602
- 34. ShinyStanの起動 [TdSdk%eZ[ kefS & eeaR ad_S 9* Sg UZReZ[ kefS %X[fR ad_S &
- 37. ↑ 診断の閾値が調整できる
- 38. ↑ 診断の閾値が調整できる有効サンプル数（neff）が イテレーション数（N）の 10%以下のパラメター は自己相関が強い →thinを大に R^が1.1以上のパラメタ には収束していない chain が存在する →iter を増やす モンテカルロ標準誤差 （mcse）が パラメターの標準偏差（sd） の10%より大なら パラメターの推定値（平均値） の信頼性が低い →chain、iter を増やす 有効サンプル数 MCMC系列の 自己相関の強さ モンテカルロ標準誤差 パラメターの推定値 （平均値）の信頼性 R hat MCMC系列が 収束しているか
- 39. ↑ 診断の閾値が調整できる 全てのパラメターが収束していないと 正しい事後分布は得られない 有効サンプル数（neff）が イテレーション数（N）の 10%以下のパラメター は自己相関が強い →thinを大に R^が1.1以上のパラメタ には収束していない chain が存在する →iter を増やす モンテカルロ標準誤差 （mcse）が パラメターの標準偏差（sd） の10%より大なら パラメターの推定値（平均値） の信頼性が低い →chain、iter を増やす 有効サンプル数 MCMC系列の 自己相関の強さ モンテカルロ標準誤差 パラメターの推定値 （平均値）の信頼性 R hat MCMC系列が 収束しているか
- 40. MCMC系列の自己相関 ←表示するパラメターを選択 mu sigma lp__ chain 1 chain 2 chain 3 chain 4 Flip facet で パラメターとチェインの 表示を入れ替えている 図をggplot2オブジェクトや pdfとして書き出せる ラグ 相関 係数
- 41. Stanの文法
- 42. Stanコードの構成 Xg Uf[a e mn ,, VSfS mn ,,IfS r fdS eXad_ V VSfSmn ,, r bSdS_ f de mn ,, r fdS eXad_ V bSdS_ f demn ,, r _aV mn ,, Y dSf V cgS f[f[ e mn ,, r ,, 必須なのは _aV のみ、ブロックの順番を変えてはいけない bSdS_ f de) fdS eXad_ V bSdS_ f de) Y dSf V cgS f[f[ e で定義した値が出力される fdS eXad_ V bSdS_ f de 以降がイテレーション毎に実行される
- 43. 基本的なデータ型 ,, r [ f <8 ,,、 d S =8 ,, ,, q u p ~ v h UfadP.- L8 ,, _Sfd[jP<)< E8 ,, daiRh UfadP.- L/8 ,, ,, u v [ f9 ai d:.; >8 d S 9 ai d:-) gbb d:.-; 8 h Ufad9 ai d:_[ %L&) gbb d:_Sj%L&; 8 ,, u ~ v [ f MPF 8 ,,. 、 d S NP/)/)/ 8 ,,0 _Sfd[jP/)/ P0)0 8 ,,/j/ p0j0 ,,w
- 44. model ブロック _aV m _g o ad_S %-) .---&8 ,, e[Y_S o g [Xad_%-) .---&8 ,, k o ad_S %_g) e[Y_S&8 ,, u v n 実際には対数確率をひたすら足し上げている パラメタと観測値の分布を指定する f(θ|y) = C×f(y|θ)f(θ) log(f(θ|y)) = log(C)+log(f(y|θ))+log(f(θ)) HMCは対数事後確率関数をθで微分した傾きを利用するので θに依存しない定数項は省略されてる場合もある （log(C)やf(θ)内の正規化係数など）
- 45. model ブロック k o ZaY %fZ fS&8 //Sampling Statement [ Ud _ fR aYRbdaT% ZaY R aY% k) fZ fS& &8 bRR 9* bRR ( ZaY R aY% k) fZ fS &8w Stanでは 確率分布関数 hoge に対して 対数確率を足し上げる３つの等価な書き方がある aY% ZaY %& & ー Sampling Statement が使えない時は [ Ud _ fR aYRbdaT% & ※lp__ は将来的にはなくなるので推奨されない
- 46. モデルの記述例
- 47. 線形回帰 VSfS m [ f9 ai d:-; F8 ,, [ f9 ai d:.; C8 ,, ・ ” _Sfd[jPF)C j8 ,, ・ ” h UfadPF k8 ,, ” n bSdS_ f de m d S S bZS8 ,, （ h UfadPC T fS8 ,, r d S 9 ai d:-; e[Y_S8 ,, “ n _aV m ,, k o ad_S %S bZS ( j T fS) e[Y_S&8 ,, ~ ,,Xad%[ [ .7F& ,, kP[ o ad_S %S bZS ( jP[ T fS) e[Y_S&8 n
- 48. 階層ベイズモデル y a b[1] s 普通のベイズ統計モデル 階層ベイズモデル パラメターに対して、ハイパーパラメターを使って （経験に基づいた）情報的な事前分布を設定する。 →パラメターに制約を課すことで推定が可能になる。 b[K]… y a b[1] b[K]… 無情報 無情報 無情報 無情報 無情報 パラメタ数が多すぎると推定できない…. パラメター 観測値 ハイパー パラメター
- 50. テストの点数の分布へのあてはめ、各生徒の解答力の推定 VSfS m [ f9 ai d:-; F8 ,, F [ f9 ai d:-; E8 ,, E [ f9 ai d:-; kPF 8 ,, k n bSdS_ f de m d S 9 ai d:-; S bZS8 ,, S bZS d S T fSPF 8 ,, T fS d S 9 ai d:-; e[Y_S8 ,,T fS “ e[Y_S n fdS eXad_ V bSdS_ f de m d S lPF 8 d S bPF 8 Xad%[ [ .7F& m lP[ 9* S bZS ( T fSP[ 8 ,, l bP[ 9* [ hR aY[f% lP[ &8 ,, }x b n n _aV m T fS o ad_S %-) e[Y_S&8 ,, u v Xad%[ [ .7F& kP[ o T[ a_[S %E) bP[ &8 ,, k u wv n ※ある問に正答する確率が p のとき、M個の問題のうち、 y 個正解する確率の分布
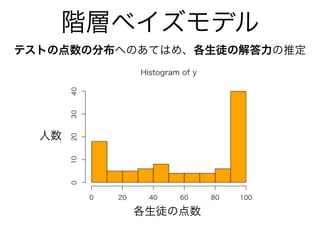
- 51. 階層ベイズモデル テストの点数の分布へのあてはめ、各生徒の解答力の推定 実測● 予測● 各生徒のテストの点数 人数 Y dSf V cgS f[f[ em [ f kRZSfPF 8 ,, k Xad%[ [ .7F& kRZSfP[ 9* T[ a_[S Rd Y%E) bP[ &8,, n
- 52. 階層ベイズモデル テストの点数の分布へのあてはめ、各生徒の解答力の推定 実測● 予測● 各生徒の解答力 z 人数 Y dSf V cgS f[f[ em [ f kRZSfPF 8 ,, k Xad%[ [ .7F& kRZSfP[ 9* T[ a_[S Rd Y%E) bP[ &8,, n
- 54. ベイズ統計モデリング入門書 道具としてのベイズ統計（涌井良幸） ベイズ統計、MCMC法 基礎からのベイズ統計学（豊田秀樹ら） ベイズ統計、ハミルトニアン・モンテカルロ法 データ解析のための統計モデリング入門（久保拓弥） 統計モデリング Stan Modeling Language Users Guide and Reference Manual Stanの使い方、ベイズ統計モデリング これで貴方も「ベイジアン」に！
- 55. ベイズ統計モデリング入門書 道具としてのベイズ統計（涌井良幸） ベイズ統計、MCMC法 基礎からのベイズ統計学（豊田秀樹ら） ベイズ統計、ハミルトニアン・モンテカルロ法 データ解析のための統計モデリング入門（久保拓弥） 統計モデリング Stan Modeling Language Users Guide and Reference Manual Stanの使い方、ベイズ統計モデリング これで貴方も「ベイジアン」に！ 超オススメ！ 俺俺Stan manual翻訳 by siero5335
- 57. 階層ベイズモデル r r aY[ef[U 9* Xg Uf[a %j&m.+-,%.( jb%*j&&n F 9* .-- E 9* .- S bZS 9* -+53 e[Y_S 9* 0+45 “ T fS 9* d ad_%F) _ S : -) eV : e[Y_S& l 9* S bZS ( T fS b 9* aY[ef[U%l& k 9* eSbb k%b) Xg Uf[a % &mdT[ a_%.) E) &n& efS r VSfSRZ[ d 9* [ef%F: YfZ%k&) E:.-) k:k& x X[fRZ[ d 9* efS %X[ : Z[ dSdUZ[US +efS ) VSfS : VSfSRZ[ d& テストの点数の分布へのあてはめ、各生徒の解答力の推定
- 58. 階層ベイズモデル r bSdS_RZ[ d 9* jfdSUf%X[fRZ[ d& k+aTe 9* Z[ef%k) Td S]e:e c%-).--)Tk:.-&& k+bdV 9* Z[ef%Ua E S e%bSdS_RZ[ d"kRZSf&) Td S]e:e c%-).--)Tk:.-&& b af%k+aTe"_[Ve) k+aTe"Uag fe) Ua : T SU] ) bUZ:.6 ) j ST: ) k ST: & ba[ fe%k+bdV"_[Ve) k+bdV"Uag fe) Ua : d V ) bUZ:.6& l l+aTe 9* Z[ef%l) Td S]e:e c%*.2).2)Tk:/&& l+bdV 9* Z[ef%Ua E S e%bSdS_RZ[ d"l&) Td S]e:e c%*.2).2)Tk:/&& b af% l+aTe"_[Ve) l+aTe"Uag fe) Ua : T SU] ) bUZ:.6 ) j ST: l ) k ST: & ba[ fe%l+bdV"_[Ve) l+bdV"Uag fe) Ua : d V ) bUZ:.6& テストの点数の分布へのあてはめ、各生徒の解答力の推定
- 59. 配列データへのアクセス ,,/j0 1j2 _Sfd[jP/)0 P1)2 8 ,, j. 9* P1)2)/)0 8 ,,d S j/ 9* P1)2)/ 8 ,,daiRh UfadP0 j0 9* P1)2 8 ,,_Sfd[jP/)0 j1 9* P1 8 ,,_Sfd[jP/)0 ,, 2 . ,,j2 9* P1)2) )0 ,,h UfadP/ z ~ ,, z Xad%[ [ .7/& j2P[ 9* P1)2)[)0 8 ,, z y ,, P. P/ P.)/
- 60. ロジスティック回帰 VSfS m [ f9 ai d:.; F8 ,, r [ f9 ai d:-; C8 ,, ・ ” _Sfd[jPF)C j8 ,, [ f9 ai d:-) gbb d:.; kPF 8 ,, ” - ad .uw v n bSdS_ f de m d S S bZS8 ,, （ h UfadPC T fS8 ,, n _aV m k o T d ag [R aY[f%S bZS ( j T fS&8 ,, ~ ,,Xad % [ .7F& ,,kP o T d ag [%[ hR aY[f%S bZS ( T fS jP &&8 n （※注）ハマりポイント bernoulli（ベルヌーイ）分布は0か1（つまり整数）しか 返さないのに y を vector（実数）で定義してしまうと コンパイルエラーになる 線形回帰との違いを赤で示している ,,[ hR aY[f aY[ef[U
- 61. 予測値の算出① ,, $ VSfS m [ f9 ai d:-; F8 ,, [ f9 ai d:.; C8 ,, ・ ” _Sfd[jPF)C j8 ,, ・ ” u r v h UfadPF k8 ,, ” u r v ,, ・ ” [ f9 ai d:-; FR i8 ,, _Sfd[jPFR i) C jR i8 ,,・ ” u r v n bSdS_ f de m d S S bZS8 ,, （ h UfadPC T fS8 ,, r d S 9 ai d:-; e[Y_S8 ,, n _aV m k o ad_S %S bZS ( j T fS) e[Y_S&8 n Y dSf V cgS f[f[ e m h UfadPFR i kR i8 Xad % [ .7FR i& kR iP 9* ad_S Rd Y%jR iP T fS) e[Y_S&8 n Y dSf V cgS f[f[ e で算出する方法 可能な場合はこちらのほうが良い、有効サンプル数が大きくなる ,, r r y ,, k
- 62. 予測値の算出② ,, $ VSfS m [ f9 ai d:-; F8 ,, [ f9 ai d:.; C8 ,, ・ ” _Sfd[jPF)C j8 ,, ・ ” u r v h UfadPF k8 ,, ” u r v ,, ・ ” [ f9 ai d:-; FR i8 ,, _Sfd[jPFR i) C jR i8 ,,・ ” u r v n bSdS_ f de m d S S bZS8 ,, （ h UfadPC T fS8 ,, r d S 9 ai d:-; e[Y_S8 ,, ,, k r h UfadPFR i kR i8 n _aV m k o ad_S %S bZS ( j T fS) e[Y_S&8 ,, kR i o ad_S %S bZS ( j T fS) e[Y_S&8 n _aV で算出する方法