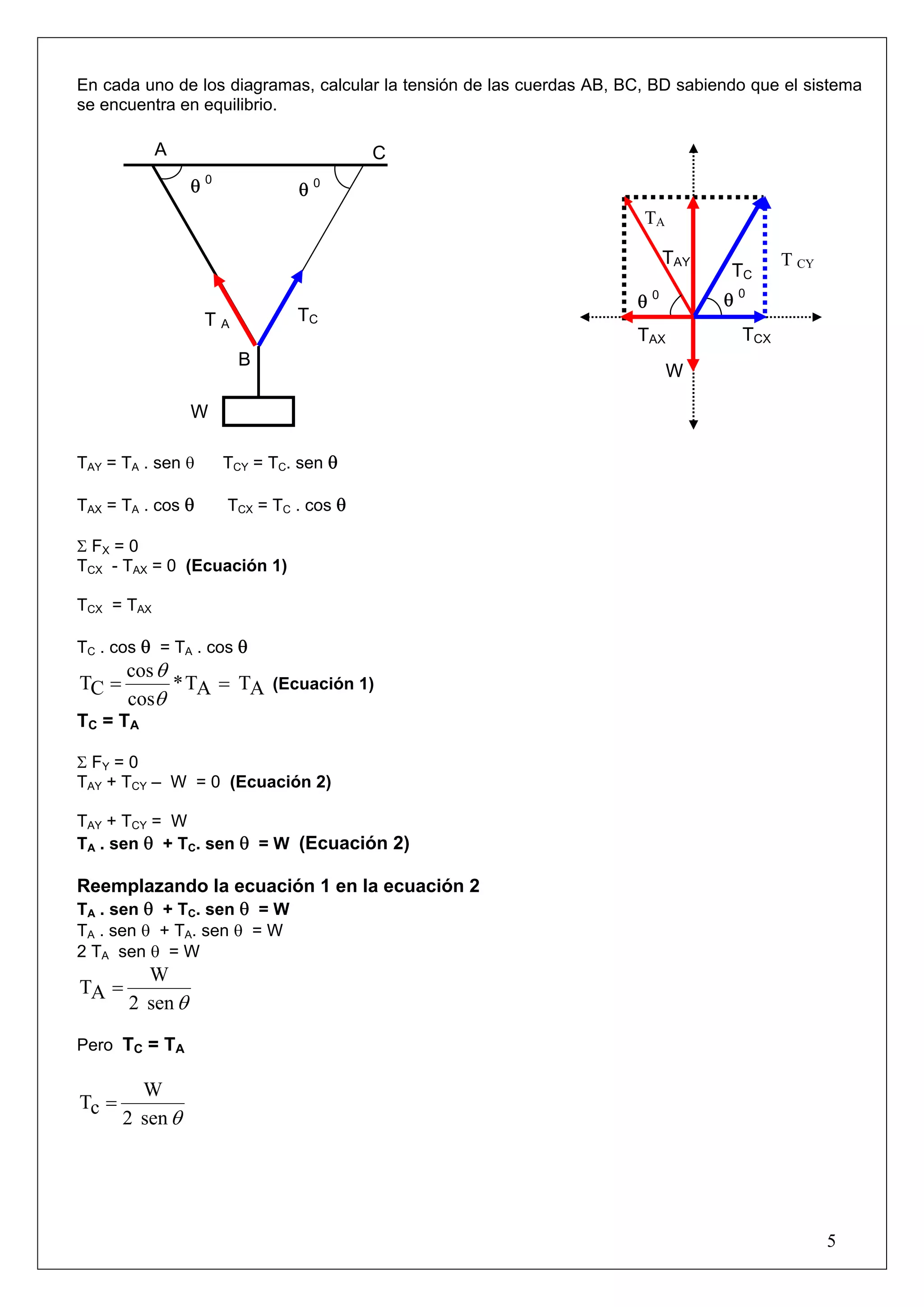
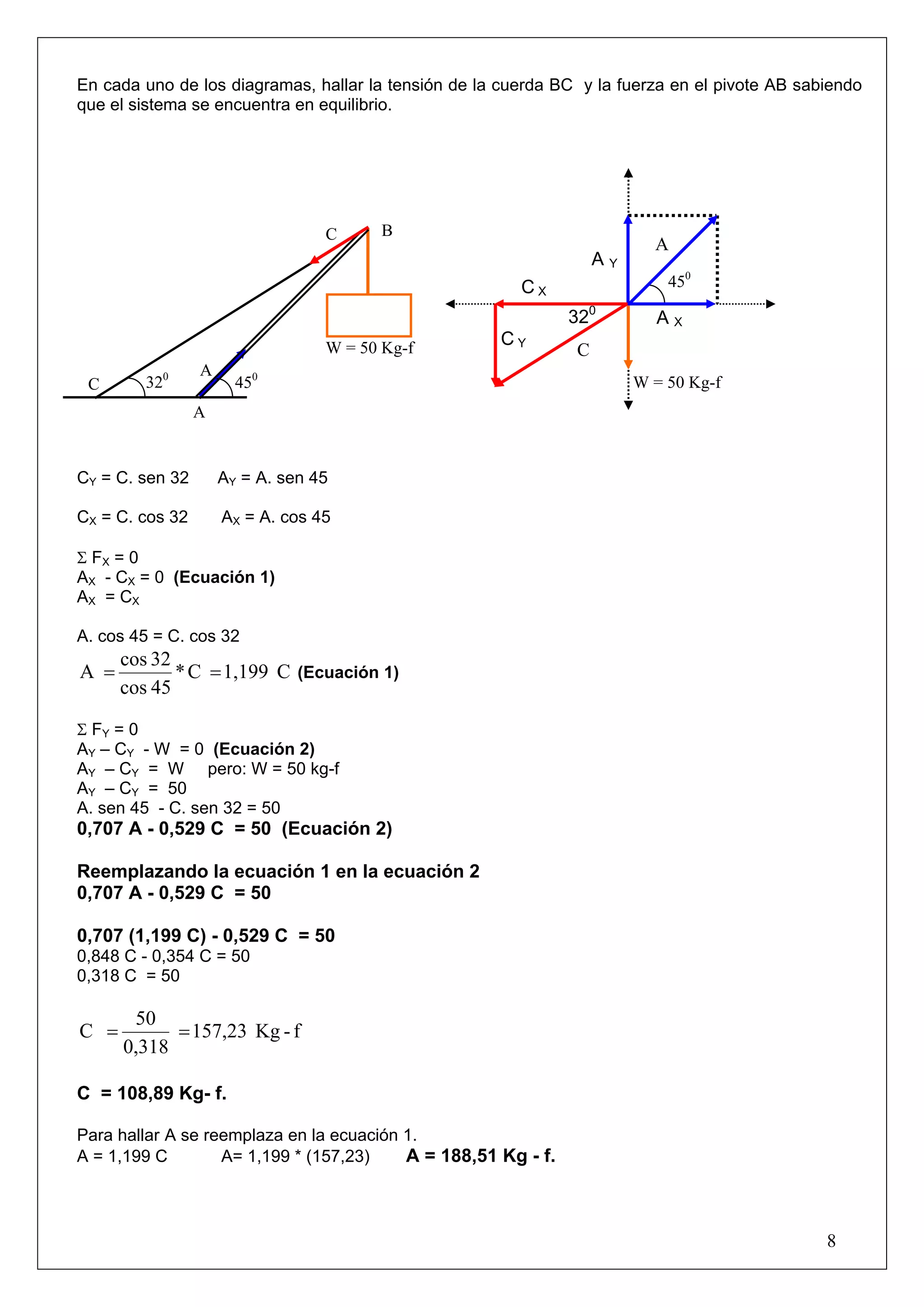
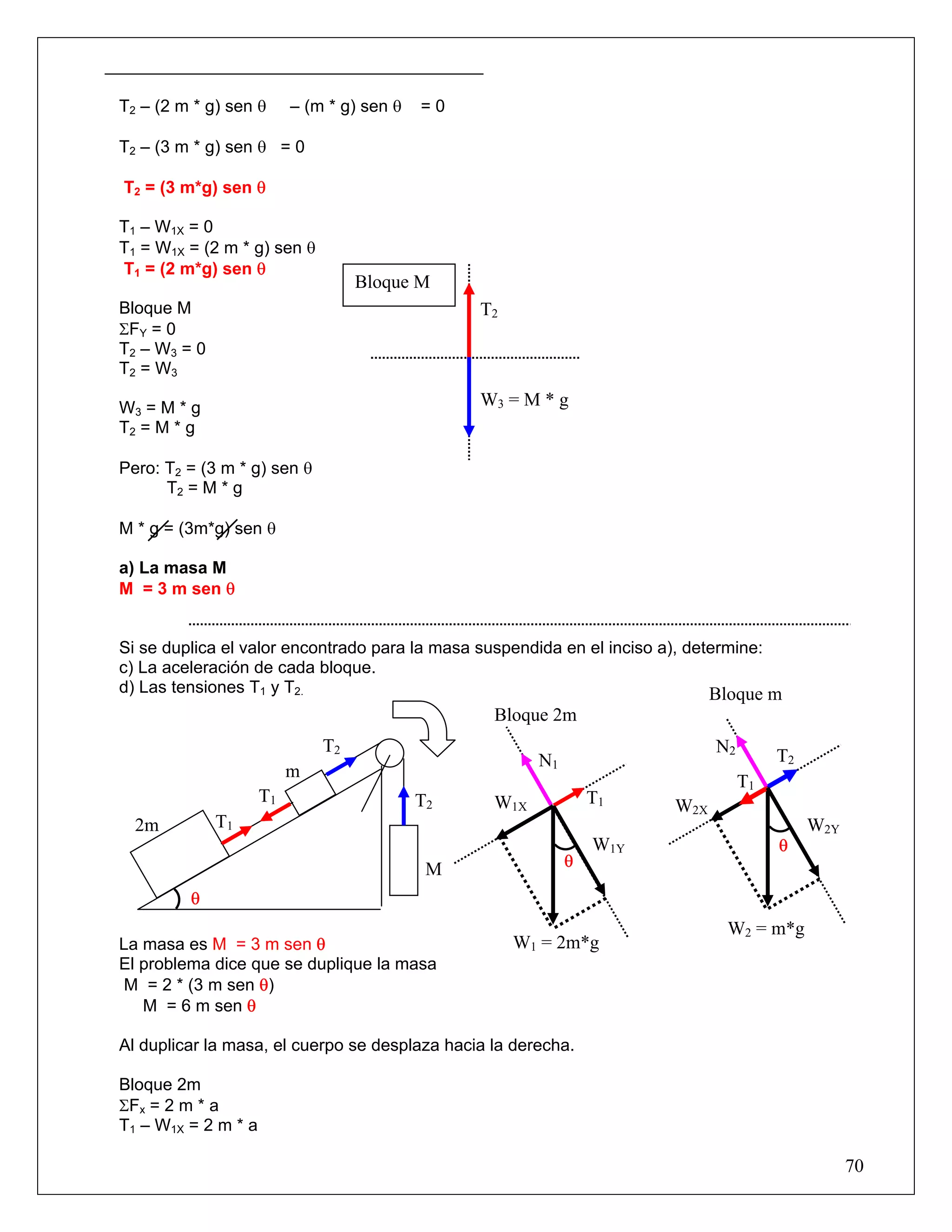
El documento presenta tres bloques de diferentes masas unidos por cuerdas. Se calculan las tensiones de las cuerdas y la aceleración del sistema mediante la aplicación de las leyes de Newton. Se obtienen tres ecuaciones de equilibrio que relacionan las fuerzas actuantes sobre cada bloque y se resuelven para hallar la aceleración y las tensiones de las cuerdas.






























![FR = μ * N1 (Ecuación 3)
FR = 1/7 * (14 cos θ)
FR = 2 cos θ
Bloque m2
Σ FY = 0
P2 – T = 0 (Ecuación 4)
P2 = T Pero: P2 = 10 kg
T = P2 = 10 kg
Reemplazando en la ecuación 1
T – P1X – FR = 0 (Ecuación 1)
10 – 14 senθ - 2 cos θ = 0
pero : sen2 θ + cos2 θ = 1
1/ 2
cosθ = 1 - sen 2θ = ⎛1 - sen 2 θ ⎞
⎜ ⎟
⎝ ⎠
Reemplazando
10 – 14 senθ - 2 cos θ = 0
10 – 14 senθ - 2 (1-sen2 θ)1/2 = 0
5– 7 senθ - (1-sen2 θ)1/2 = 0
5– 7 senθ = (1-sen2 θ)1/2
Elevando al cuadrado en ambos lados
2
⎡ 1/ 2 ⎤
[5 − 7 senθ ]2 = ⎢⎛1 - sen 2 θ ⎞
⎜ ⎟ ⎥
⎢⎝
⎣
⎠ ⎥
⎦
25 – 70 senθ + 49 sen2 θ = 1 – sen2 θ
49 sen2 θ + sen2 θ – 70 senθ + 25 – 1 = 0
50 sen2 θ – 70 sen θ + 24 = 0
Aplicando la formula para ecuaciones de segundo grado.
- (- 70) ± ( - 70) 2 - 4 (50) 24 70 ± 4900 - 4800
sen θ = =
2 (50) 100
70 ± 100 70 ± 10
sen θ = =
100 100
70 + 10 80
sen θ1 = = = 0,8 θ1 = arc sen 0,8 θ1 = 53,130
100 100
70 − 10 60
sen θ 2 = = = 0,6 θ2 = arc sen 0,6 θ2 = 36,860
100 100
θ1 = 53,130 Cuando el cuerpo se desplaza hacia la derecha.
θ2 = 36,860 Cuando el cuerpo se desplaza hacia la izquierda.
33](https://image.slidesharecdn.com/problemas-resueltos-newton-110805201603-phpapp01/75/Problemas-resueltos-newton-33-2048.jpg)






















































![⎡ m M T + m 2 m1 T + m1 M T ⎤
m2 g = ⎢ 2 ⎥
⎣ m1 M ⎦
( m1 M)* m 2 g = [ m2 M + m 2 m1 + m1 M ] T
(m1
M)
* m2 g = T
m 2 M + m 2 m1 + m1 M
⎡ m1 M ⎤
T = ⎢ ⎥ * m2 g
⎣ m 2 M + m 2 m1 + m1 M ⎦
SERWAY CAPITULO 5 LAS LEYES DEL MOVIMIENTO
Problema 5-85 Los tres bloques de la figura están conectados por medio de cuerdas sin masa
que pasan por poleas sin fricción. La aceleración del sistema es 2,35 cm/seg2 a la izquierda y las
superficies son rugosas. Determine:
a) Las tensiones en la cuerda
b) El coeficiente de fricción cinético entre los bloques y las superficies (Supóngase la misma
μ para ambos bloques)
m2
T1 T2
T2
m3
T1
FR2
FR3
250
m1
Datos: m1 = 10 kg. m2 = 5 kg. m3 = 3 kg a = 2,35 cm/seg2 g = 9,8 m/seg2
Bloque m1 Bloque m2
Bloque m3
T1 N2 N3
T2
T1 FR2 T2
P3X
FR3
P3Y
P1 = m1 g P2 = m2 g
250
Bloque m1
∑ FY = m1 a
P1 – T1 = m1 a (Ecuación 1) P3 = m3 g
P1 = m1 g
P1 = 10 * 9,8 = 98 Newton
89](https://image.slidesharecdn.com/problemas-resueltos-newton-110805201603-phpapp01/75/Problemas-resueltos-newton-89-2048.jpg)
















