El documento presenta información sobre la literatura boliviana y latinoamericana del siglo XX. Se menciona a importantes autores bolivianos como Ricardo Jaimes Freyre, Franz Tamayo y María Josefa Mujía. También se describen diferentes géneros literarios como la novela realista, la novela de la Guerra del Chaco y la novela naturalista. Por último, se hace referencia al boom de la literatura latinoamericana en la década de 1960 y 1970, con obras emblemáticas como Cien Años de Soledad de Gabriel García Márquez.


























![COMUNIDAD Y SOCIEDAD Comunicación y Lenguajes
SEGUNDO
TRIMESTRE
25
Uso de la “Y” y la “LL”
Leamos el siguiente texto:
otra temporada me dio por combinar el uso de mAyÚsCuLaS cOn MiNúScUlAs, lo cual era muy tardado, y también
llegué a escribir con contracciones al
“No estoy en contra de estos usos ni los repruebo: los idiomas son organismos vivos, complejos que no
Por eso, no es raro que alguien le haya propuesto a la Real Academia de
Botella de mar para el Dios de las palabras.
«Nuestra contribución no debería ser la de meterla en cintura [a la lengua], sino
«Humanicemos sus leyes, aprendamos de las lenguas indígenas a las que
asimilemos pronto y bien los neologismos técnicos y científicos antes de que se
nos infiltren sin digerir, negociemos de buen corazón con los gerundios bárbaros,
que dos o tres lingüistas y académicos se llevaban las manos a la boca o se
desmayaban:
Uso de la “Y” y la “LL”
¿Por qué Gabriel García
Glosario
Alteración de la
capacidad de leer por la que
orden de letras, sílabas o
idea que se da como cierta
y que sirve de base a un
La Academia Sueca le
otorgó el Premio Nobel de
Literatura a Gabriel García](https://image.slidesharecdn.com/quinto-221219020539-f034d862/75/QUINTO-pdf-27-2048.jpg)


![Ministerio de Educación
SEGUNDO
TRIMESTRE
28
Completamos con “LL” o “Y”, según convenga:
libros que había en el resto de las habitaciones […]”
experiencia,
¡Apliquemos lo aprendido!
Ejemplo:
EL INFORME, EL ACTA Y LA SOLICITUD
Felipillo – Cuaresmilla – tornillos – camilla – cuclillas – grillos – membrillo –
EL INFORME, EL ACTA Y LA SOLICITUD](https://image.slidesharecdn.com/quinto-221219020539-f034d862/75/QUINTO-pdf-30-2048.jpg)






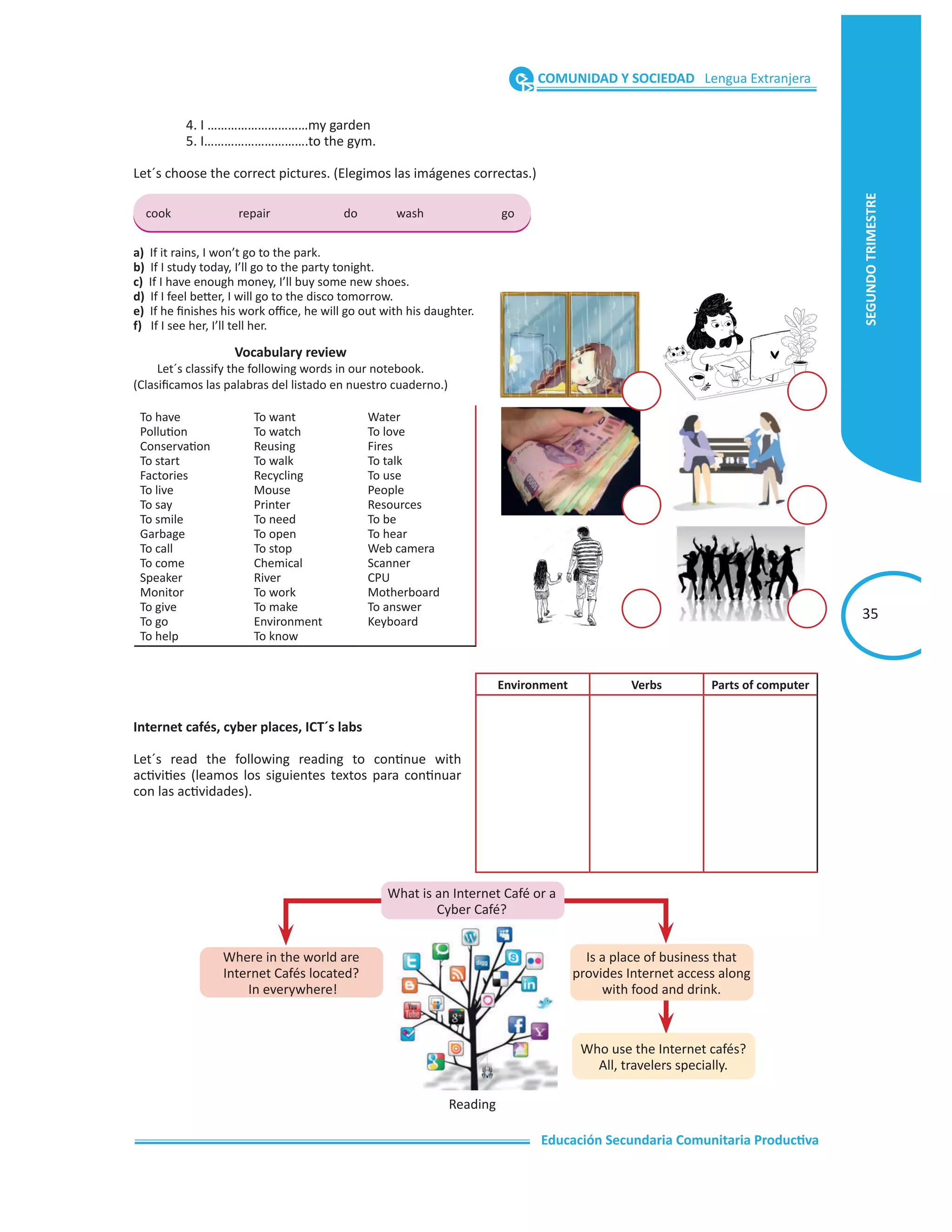













































































































![VIDA TIERRA Y TERRITORIO Física
SEGUNDO
TRIMESTRE
145
Solución
Con la 2da. Ley de Newton hallamos la aceleración.
Por cinemática, hallamos la distancia recorrida.
Como el ladrillo se detiene la velocidad final es cero:
De la ecuación del trabajo (ecuación 1):
Reemplazamos los datos en la ecuación anterior.
Para el trabajo efectuado por la fuerza gravitacional sobre m
Datos
d = 5 m
= 37° + 90°
g = 9,8 m/s2
Wm = ¿?
Un ladrillo de 4 kg de masa es lanzado horizontalmente sobre una superficie
rugosa con una velocidad inicial de 10 m/s, como se muestra en la figura.
Hallamos el trabajo realizado por la fuerza de rozamiento cinético sobre el ladrillo
hasta el instante en que se detiene. (Consideramos que g = 10 [m/s2
]).
Datos
v = 10 m/s
m = 4 kg
c = 0.5
= 180°
g = 10 m/s2
Wm = ¿?
Solución
Con la 2da ley de Newton.
Hallamos la fuerza gravitatoria sobre m.
Fg = mg Fg = (1kg) (9,8m/s2)
Fg = 9,8 N
De la ecuación del trabajo (ecuación 1):
Reemplazamos los datos en la ecuación anterior.
Fg
N
frc
w
N
NOTA:
4 m
m
Solución
Con la 2da. Ley de Newton hallamos la aceleración.
Por cinemática, hallamos la distancia recorrida.
Como el ladrillo se detiene la velocidad final es cero:
De la ecuación del trabajo (ecuación 1):
Reemplazamos los datos en la ecuación anterior.
Para el trabajo efectuado por la fuerza gravitacional sobre m
Datos
d = 5 m
= 37° + 90°
g = 9,8 m/s2
Wm = ¿?
Un ladrillo de 4 kg de masa es lanzado horizontalmente sobre una superficie
rugosa con una velocidad inicial de 10 m/s, como se muestra en la figura.
Hallamos el trabajo realizado por la fuerza de rozamiento cinético sobre el ladrillo
hasta el instante en que se detiene. (Consideramos que g = 10 [m/s2
]).
Datos
v = 10 m/s
m = 4 kg
c = 0.5
= 180°
g = 10 m/s2
Wm = ¿?
Solución
Con la 2da ley de Newton.
Hallamos la fuerza gravitatoria sobre m.
Fg = mg Fg = (1kg) (9,8m/s2)
Fg = 9,8 N
De la ecuación del trabajo (ecuación 1):
Reemplazamos los datos en la ecuación anterior.
Fg
N
frc
w
N
NOTA:
4 m
m
Solución
Con la 2da. Ley de Newton hallamos la aceleración.
Por cinemática, hallamos la distancia recorrida.
Como el ladrillo se detiene la velocidad final es cero:
De la ecuación del trabajo (ecuación 1):
Reemplazamos los datos en la ecuación anterior.
Para el trabajo efectuado por la fuerza gravitacional sobre m
Datos
d = 5 m
= 37° + 90°
g = 9,8 m/s2
Wm = ¿?
Un ladrillo de 4 kg de masa es lanzado horizontalmente sobre una superficie
rugosa con una velocidad inicial de 10 m/s, como se muestra en la figura.
Hallamos el trabajo realizado por la fuerza de rozamiento cinético sobre el ladrillo
hasta el instante en que se detiene. (Consideramos que g = 10 [m/s2
]).
Datos
v = 10 m/s
m = 4 kg
c = 0.5
= 180°
g = 10 m/s2
Wm = ¿?
Solución
Con la 2da ley de Newton.
Hallamos la fuerza gravitatoria sobre m.
Fg = mg Fg = (1kg) (9,8m/s2)
Fg = 9,8 N
De la ecuación del trabajo (ecuación 1):
Reemplazamos los datos en la ecuación anterior.
Fg
N
frc
w
N
NOTA:
4 m
m
como se
observa el trabajo
4 m
m es](https://image.slidesharecdn.com/quinto-221219020539-f034d862/75/QUINTO-pdf-147-2048.jpg)
![Ministerio de Educación
SEGUNDO
TRIMESTRE
146
3. Trabajo efectuado por una fuerza variable, realizado por un resorte (Ley de Hooke)
Por lo general, las fuerzas son variables, eso significa que cambian con el tiempo y/o la posición. Si una fuerza
variable F logra mover a un objeto un cierto desplazamiento, no podremos utilizar la ecuación (1). En este
caso, el cuerpo experimenta pequeños desplazamientos, y de alguna forma, debemos considerar, durante
ese intervalo, que la fuerza aplicada es aproximadamente constante.
Un ejemplo muy común es realizar el trabajo cuando estiramos un resorte. En este caso, mientras el resorte
está elongado, o comprimido cada vez más, la fuerza de restauración de dicho resorte se hace más grande.
Por lo tanto, es necesario aplicar una fuerza mayor. Podemos decir que la fuerza aplicada F es directamente
proporcional al desplazamiento o al cambio de longitud del resorte.
Esto se puede expresar en forma de ecuación:
F = k x = k(x – xo)
Sí Xo = 0 F = kx …(1.2) k es la constante de elasticidad del resorte.
Podemos apreciar que la fuerza F varía conforme varia x. Esto se describe diciendo que la fuerza es una
función de la posición. En todo caso mientras mayor sea el valor de , más rígido o fuerte será el resorte. Las
unidades de son [N/m].
La ecuación (1.2) se cumple generalmente con resortes ideales. Ahora bien, los resortes reales se aproximan
a una relación lineal entre fuerza y desplazamiento, esto dentro de ciertos límites. En nuestro análisis se
puede observar que el resorte ejerce una fuerza igual y opuesta. Es decir, Fs k x, el signo negativo indica
que la fuerza del resorte está en dirección opuesta al desplazamiento. Este principio se conoce como la Ley
de Hooke.
En la gráfica de F vs x, la pendiente de la línea es igual a k, y F se
incrementa uniformemente con x. Entonces la fuerza promedio es:
Si Fo = 0
Trabajo realizado por una fuerza que
varia en forma uniforme.](https://image.slidesharecdn.com/quinto-221219020539-f034d862/75/QUINTO-pdf-148-2048.jpg)
![VIDA TIERRA Y TERRITORIO Física
SEGUNDO
TRIMESTRE
147
Así, el trabajo realizado al estirar o comprimir el resorte es:
Como F = kx, entonces:
… (1.2)
En la vida diaria, el término trabajo significa realizar alguna actividad que
genere ganancia monetaria. En Física el trabajo tiene otro significado: se
realiza trabajo siempre que una fuerza aplicada ocasione un desplazamiento.
La aplicación de mayor fuerza debe dar como resultado más trabajo. Del
mismo modo, aplicar una misma fuerza a una mayor distancia debe resultará
en mayor trabajo realizado.
Un ejemplo de aplicación de trabajo, en la vida diaria, se da cuando alguien
levanta un objeto del suelo. En este caso se realiza trabajo porque se aplica
una fuerza vertical para conseguir un desplazamiento en la misma dirección.
Apliquemos los conocimientos aprendidos:
Un joven jala un carrito que tiene una cierta masa. En el primer caso, el joven
jala el carrito con una fuerza de 20 [N] y con un ángulo de 60°.
En el segundo caso, el joven jala con un ángulo de 0° y aplica, al igual que
primer caso, una fuerza de 20 [N].
Determinamos, en ambos casos, el trabajo realizado, producto de la fuerza
que ejerce el joven al jalar el carrito cuando se recorre un total de 8 [m].
x: Representa la variación de
la distancia recorrida.
Así, el trabajo realizado al estirar o comprimir el resorte es:
Como F = kx, entonces:
… (1.2)
En la vida diaria, el término trabajo significa realizar alguna actividad que
genere ganancia monetaria. En Física el trabajo tiene otro significado: se
realiza trabajo siempre que una fuerza aplicada ocasione un desplazamiento.
La aplicación de mayor fuerza debe dar como resultado más trabajo. Del
mismo modo, aplicar una misma fuerza a una mayor distancia debe resultará
en mayor trabajo realizado.
Un ejemplo de aplicación de trabajo, en la vida diaria, se da cuando alguien
levanta un objeto del suelo. En este caso se realiza trabajo porque se aplica
una fuerza vertical para conseguir un desplazamiento en la misma dirección.
Apliquemos los conocimientos aprendidos:
Un joven jala un carrito que tiene una cierta masa. En el primer caso, el joven
jala el carrito con una fuerza de 20 [N] y con un ángulo de 60°.
En el segundo caso, el joven jala con un ángulo de 0° y aplica, al igual que
primer caso, una fuerza de 20 [N].
Determinamos, en ambos casos, el trabajo realizado, producto de la fuerza
que ejerce el joven al jalar el carrito cuando se recorre un total de 8 [m].
x: Representa la variación de
la distancia recorrida.
Así, el trabajo realizado al estirar o comprimir el resorte es:
Como F = kx, entonces:
… (1.2)
En la vida diaria, el término trabajo significa realizar alguna actividad que
genere ganancia monetaria. En Física el trabajo tiene otro significado: se
realiza trabajo siempre que una fuerza aplicada ocasione un desplazamiento.
La aplicación de mayor fuerza debe dar como resultado más trabajo. Del
mismo modo, aplicar una misma fuerza a una mayor distancia debe resultará
en mayor trabajo realizado.
Un ejemplo de aplicación de trabajo, en la vida diaria, se da cuando alguien
levanta un objeto del suelo. En este caso se realiza trabajo porque se aplica
una fuerza vertical para conseguir un desplazamiento en la misma dirección.
Apliquemos los conocimientos aprendidos:
Un joven jala un carrito que tiene una cierta masa. En el primer caso, el joven
jala el carrito con una fuerza de 20 [N] y con un ángulo de 60°.
En el segundo caso, el joven jala con un ángulo de 0° y aplica, al igual que
primer caso, una fuerza de 20 [N].
Determinamos, en ambos casos, el trabajo realizado, producto de la fuerza
que ejerce el joven al jalar el carrito cuando se recorre un total de 8 [m].
x: Representa la variación de
la distancia recorrida.
Así, el trabajo realizado al estirar o comprimir el resorte es:
Como F = kx, entonces:
… (1.2)
En la vida diaria, el término trabajo significa realizar alguna actividad que
genere ganancia monetaria. En Física el trabajo tiene otro significado: se
realiza trabajo siempre que una fuerza aplicada ocasione un desplazamiento.
La aplicación de mayor fuerza debe dar como resultado más trabajo. Del
mismo modo, aplicar una misma fuerza a una mayor distancia debe resultará
en mayor trabajo realizado.
Un ejemplo de aplicación de trabajo, en la vida diaria, se da cuando alguien
levanta un objeto del suelo. En este caso se realiza trabajo porque se aplica
una fuerza vertical para conseguir un desplazamiento en la misma dirección.
Apliquemos los conocimientos aprendidos:
Un joven jala un carrito que tiene una cierta masa. En el primer caso, el joven
jala el carrito con una fuerza de 20 [N] y con un ángulo de 60°.
En el segundo caso, el joven jala con un ángulo de 0° y aplica, al igual que
primer caso, una fuerza de 20 [N].
Determinamos, en ambos casos, el trabajo realizado, producto de la fuerza
que ejerce el joven al jalar el carrito cuando se recorre un total de 8 [m].
x: Representa la variación de
la distancia recorrida.
Así, el trabajo realizado al estirar o comprimir el resorte es:
Como F = kx, entonces:
… (1.2)
En la vida diaria, el término trabajo significa realizar alguna actividad que
genere ganancia monetaria. En Física el trabajo tiene otro significado: se
realiza trabajo siempre que una fuerza aplicada ocasione un desplazamiento.
La aplicación de mayor fuerza debe dar como resultado más trabajo. Del
mismo modo, aplicar una misma fuerza a una mayor distancia debe resultará
en mayor trabajo realizado.
Un ejemplo de aplicación de trabajo, en la vida diaria, se da cuando alguien
levanta un objeto del suelo. En este caso se realiza trabajo porque se aplica
una fuerza vertical para conseguir un desplazamiento en la misma dirección.
Apliquemos los conocimientos aprendidos:
Un joven jala un carrito que tiene una cierta masa. En el primer caso, el joven
jala el carrito con una fuerza de 20 [N] y con un ángulo de 60°.
En el segundo caso, el joven jala con un ángulo de 0° y aplica, al igual que
primer caso, una fuerza de 20 [N].
Determinamos, en ambos casos, el trabajo realizado, producto de la fuerza
que ejerce el joven al jalar el carrito cuando se recorre un total de 8 [m].
x: Representa la variación de
la distancia recorrida.
Así, el trabajo realizado al estirar o comprimir el resorte es:
Como F = kx, entonces:
… (1.2)
En la vida diaria, el término trabajo significa realizar alguna actividad que
genere ganancia monetaria. En Física el trabajo tiene otro significado: se
realiza trabajo siempre que una fuerza aplicada ocasione un desplazamiento.
La aplicación de mayor fuerza debe dar como resultado más trabajo. Del
mismo modo, aplicar una misma fuerza a una mayor distancia debe resultará
en mayor trabajo realizado.
Un ejemplo de aplicación de trabajo, en la vida diaria, se da cuando alguien
levanta un objeto del suelo. En este caso se realiza trabajo porque se aplica
una fuerza vertical para conseguir un desplazamiento en la misma dirección.
Apliquemos los conocimientos aprendidos:
Un joven jala un carrito que tiene una cierta masa. En el primer caso, el joven
jala el carrito con una fuerza de 20 [N] y con un ángulo de 60°.
En el segundo caso, el joven jala con un ángulo de 0° y aplica, al igual que
primer caso, una fuerza de 20 [N].
Determinamos, en ambos casos, el trabajo realizado, producto de la fuerza
que ejerce el joven al jalar el carrito cuando se recorre un total de 8 [m].
x: Representa la variación de
la distancia recorrida.](https://image.slidesharecdn.com/quinto-221219020539-f034d862/75/QUINTO-pdf-149-2048.jpg)
![Ministerio de Educación
SEGUNDO
TRIMESTRE
148
Con los mismos datos, calcular el trabajo neto del caso 1 y caso 2, considerando que la masa del
objeto es 10 [kg] y 30 [kg], respectivamente. El coeficiente de rozamiento es 0,5 en ambos casos.
Si la masa del objeto del segundo caso es igual al segundo. ¿En cuál caso realizaríamos mayor trabajo,
por qué?
La energía mecánica sostenible y sustentable en la comunidad
Las consecuencias del trabajo…
Realizamos los siguientes experimentos:
- En las figuras 1 y 2 observamos movimiento. ¿En qué se diferencia cada uno de estos?
1. Concepto de energía
En la Física clásica, específicamente la mecánica, la energía es
la capacidad de trabajo de un objeto. Además, sostiene que la
cantidad de energía contenida en un sistema cerrado es constante
(siempre es la misma), pero lo interesante es que puede
transformarse y puede transferirse de una partícula a otra. Por lo
tanto, la energía es la capacidad de un cuerpo o sistema para realizar
un determinado trabajo.
Con los mismos datos, calcular el trabajo neto del caso 1 y caso 2, considerando que la masa del
objeto es 10 [kg] y 30 [kg], respectivamente. El coeficiente de rozamiento es 0,5 en ambos casos.
Si la masa del objeto del segundo caso es igual al segundo. ¿En cuál caso realizaríamos mayor trabajo,
por qué?
La energía mecánica sostenible y sustentable en la comunidad
Las consecuencias del trabajo…
Realizamos los siguientes experimentos:
- En las figuras 1 y 2 observamos movimiento. ¿En qué se diferencia cada uno de estos?
1. Concepto de energía
En la Física clásica, específicamente la mecánica, la energía es
la capacidad de trabajo de un objeto. Además, sostiene que la
cantidad de energía contenida en un sistema cerrado es constante
(siempre es la misma), pero lo interesante es que puede
transformarse y puede transferirse de una partícula a otra. Por lo
tanto, la energía es la capacidad de un cuerpo o sistema para realizar
un determinado trabajo.
Con los mismos datos, calcular el trabajo neto del caso 1 y caso 2, considerando que la masa del
objeto es 10 [kg] y 30 [kg], respectivamente. El coeficiente de rozamiento es 0,5 en ambos casos.
Si la masa del objeto del segundo caso es igual al segundo. ¿En cuál caso realizaríamos mayor trabajo,
por qué?
La energía mecánica sostenible y sustentable en la comunidad
Las consecuencias del trabajo…
Realizamos los siguientes experimentos:
- En las figuras 1 y 2 observamos movimiento. ¿En qué se diferencia cada uno de estos?
1. Concepto de energía
En la Física clásica, específicamente la mecánica, la energía es
la capacidad de trabajo de un objeto. Además, sostiene que la
cantidad de energía contenida en un sistema cerrado es constante
(siempre es la misma), pero lo interesante es que puede
transformarse y puede transferirse de una partícula a otra. Por lo
tanto, la energía es la capacidad de un cuerpo o sistema para realizar
un determinado trabajo.
LA ENERGÍA MECÁNICA SOSTENIBLE Y SUSTENTABLE EN LA COMUNIDAD](https://image.slidesharecdn.com/quinto-221219020539-f034d862/75/QUINTO-pdf-150-2048.jpg)

![Ministerio de Educación
SEGUNDO
TRIMESTRE
150
Son inagotables. Las energías alternativas proceden de recursos naturales, gratuitos e inagotables, al
contrario de lo que sucede con la energía generada con combustibles fósiles, procedentes de recursos
limitados y finitos.
Evitan la dependencia exterior. En algunos países, por ejemplo España, no abundan los combustibles
fósiles, el petróleo o el carbón. Estos territorios se ven obligados a vincular su abastecimiento
energético a otros países, estableciéndose así una relación de dependencia. Las energías alternativas,
por su parte, se encuentran disponibles en toda la superficie terrestre, por lo que se convierten en
grandes aliadas para impulsar la independencia energética de los territorios.
Potencian el autoconsumo. En un futuro no muy lejano, todos los edificios y construcciones deberán
ser auto suficientes en su consumo eléctrico. En muchos casos las energías alternativas pueden ser
auto producidas por el propio consumidor final.
Pueden llegar a lugares aislados. Las energías alternativas están disponibles en toda la superficie
terrestre por lo que pueden llegar a cualquier rincón del mundo, incluyendo zonas rurales o
semiurbanas.
3. Clasificación de la energía
3.1. Energía cinética
Para hablar de la energía cinética debemos de pensar en todo aquel cuerpo que posee movimiento, así sea
una persona caminando, corriendo, un autobús, un ave en pleno vuelo, la corriente del agua de un río, las
olas del mar, un disco que gira, un perro persiguiendo algún objeto, prácticamente todo aquello que esté en
movimiento recibe el nombre de energía cinética.
Si bien los cuerpos se mueven en una sola dirección (traslación) o en giros (rotación) o en una combinación
de ambos estos corresponden a una expresión de la energía cinética.
Para poder relacionar la fórmula de la energía cinética, es necesario observar qué variables influyen en la
fórmula:
...(2)
3.2. Energía potencial
La energía potencial gravitacional o gravitatoria es un tipo de energía muy importante para la física, pues se
manifiesta simplemente al levantar cualquier cuerpo a una cierta altura. Esto también ocasiona que la
persona realice un trabajo porque involucra la fuerza con la cual levanta al objeto y la altura hasta donde
consigue levantarlo.
Donde:
Ec: Energía cinética, medida en [J]
m: Masa del objeto, medida en [kg]
v: Velocidad del objeto, medida en [m/s]
Son inagotables. Las energías alternativas proceden de recursos naturales, gratuitos e inagotables, al
contrario de lo que sucede con la energía generada con combustibles fósiles, procedentes de recursos
limitados y finitos.
Evitan la dependencia exterior. En algunos países, por ejemplo España, no abundan los combustibles
fósiles, el petróleo o el carbón. Estos territorios se ven obligados a vincular su abastecimiento
energético a otros países, estableciéndose así una relación de dependencia. Las energías alternativas,
por su parte, se encuentran disponibles en toda la superficie terrestre, por lo que se convierten en
grandes aliadas para impulsar la independencia energética de los territorios.
Potencian el autoconsumo. En un futuro no muy lejano, todos los edificios y construcciones deberán
ser auto suficientes en su consumo eléctrico. En muchos casos las energías alternativas pueden ser
auto producidas por el propio consumidor final.
Pueden llegar a lugares aislados. Las energías alternativas están disponibles en toda la superficie
terrestre por lo que pueden llegar a cualquier rincón del mundo, incluyendo zonas rurales o
semiurbanas.
3. Clasificación de la energía
3.1. Energía cinética
Para hablar de la energía cinética debemos de pensar en todo aquel cuerpo que posee movimiento, así sea
una persona caminando, corriendo, un autobús, un ave en pleno vuelo, la corriente del agua de un río, las
olas del mar, un disco que gira, un perro persiguiendo algún objeto, prácticamente todo aquello que esté en
movimiento recibe el nombre de energía cinética.
Si bien los cuerpos se mueven en una sola dirección (traslación) o en giros (rotación) o en una combinación
de ambos estos corresponden a una expresión de la energía cinética.
Para poder relacionar la fórmula de la energía cinética, es necesario observar qué variables influyen en la
fórmula:
...(2)
3.2. Energía potencial
La energía potencial gravitacional o gravitatoria es un tipo de energía muy importante para la física, pues se
manifiesta simplemente al levantar cualquier cuerpo a una cierta altura. Esto también ocasiona que la
persona realice un trabajo porque involucra la fuerza con la cual levanta al objeto y la altura hasta donde
consigue levantarlo.
Donde:
Ec: Energía cinética, medida en [J]
m: Masa del objeto, medida en [kg]
v: Velocidad del objeto, medida en [m/s]](https://image.slidesharecdn.com/quinto-221219020539-f034d862/75/QUINTO-pdf-152-2048.jpg)
![VIDA TIERRA Y TERRITORIO Física
SEGUNDO
TRIMESTRE
151
Peros si observamos cuidadosamente los términos “gravitatorio” o “gravitacional”
vemos que implica el nombre de gravedad, esto es porque el origen de la energía
potencial se debe a la atracción gravitacional de la Tierra sobre el cuerpo. En todo
caso, la energía potencial se debe a la posición de un cuerpo en un campo
gravitacional.
La fórmula de la energía potencial gravitacional es muy fácil de aprender y de
identificar, matemáticamente se la expresa de la siguiente manera:
...(3)
3.3. Energía elástica
También conocida como energía potencial elástica, es la energía que se libera cuando
un muelle o un resorte comprimido, se suelta. La energía que tendrá, dependerá de
la deformación sufrida por el muelle, más deformación quiere decir más energía.
Entonces la energía potencial elástica es la que posee un resorte debido a su
elongación o compresión en un campo gravitatorio bajo la influencia de una fuerza
elástica: Fe = Kx
...(4)
3.4. Energía mecánica
Es la suma de todas las energías que posee un cuerpo o sistema:
E = Ec + Ep + Ee …(5)
Donde:
Ep: Energía potencial gravitacional, medida en [J]
m: Masa del cuerpo u objeto, medida en [kg]
g: Gravedad o valor de la constante gravitatoria, a
nivel del mar g equivale a 9,8 [m/s²]
h: Altura a la que está elevada el cuerpo u objeto,
medida en [m]
Donde:
Ee: Energía elástica, medida en [J]
x: Distancia de compresión o
elongación, medida en [m]
K: Constante de elasticidad,
medida en [N/m]
¿Qué es un resorte?](https://image.slidesharecdn.com/quinto-221219020539-f034d862/75/QUINTO-pdf-153-2048.jpg)
![Ministerio de Educación
SEGUNDO
TRIMESTRE
152
4. Teorema generalizado del trabajo y la energía
Cuando existen fuerzas no conservativas o disipativas existe una transferencia irreversible de energía:
E INICIAL = E FINAL + W Fdis … (6)
Donde:
W Fdis :Trabajo realizado por las fuerzas disipativas..
Por ejemplo, una fuerza disipativa, más usual, es la que
ejerce la fuerza de rozamiento. En este caso ya lo
estudiamos en el acápite de trabajo; pues se trata de un
trabajo negativo.
5. Ley de la conservación de la energía
En un sistema dinámico, y considerando solo la energía mecánica, es habitual que estas se manifieste de
distinta forma y se transforme en otra. La energía potencial elástica puede transformarse en cinética y esta
última en potencial gravitatoria. Cuando esto sucede en un sistema denominado conservativo, no se disipa
energía en forma de calor (no hay roce) y la cantidad de energía que posee el sistema permanece constante.
En esos sistemas ideales intervienen, exclusivamente, siempre las .
E INICIAL = E FINAL
Resolución de problemas
¿Cuál es la energía cinética de un balón de básquetbol que lleva una velocidad de 24 [m/s]?. Sabiendo
que el balón pesa 18 [N].
Datos
W = 18 N
v = 24 m/s
Solución
Recordemos que la energía cinética está dada por la ecuación (2)
En los datos, solo contamos con la velocidad, pero para hallar la masa
usamos el peso. Recordemos que W = mg
Despejando m, tenemos: m = 1,8 kg
Finalmente reemplazamos los datos en la ecuación de la energía cinética.](https://image.slidesharecdn.com/quinto-221219020539-f034d862/75/QUINTO-pdf-154-2048.jpg)
![VIDA TIERRA Y TERRITORIO Física
SEGUNDO
TRIMESTRE
153
Calcular la masa de un automóvil que viaja a una velocidad de 50 m/s, sabiendo
que la energía cinética que posee es 788 [J].
Datos
v = 50 m/s
Ec = 788887 [J]
Encontrar la energía potencial respecto a la mesa, del libro de 5to. de secundaria
que tiene una masa de aproximadamente 1,2 [kg].
Datos
Ep = ¿?
m = 1,2 kg
h = 2,3 m – 1.2 m = 1.1 m
g = 9,8 m/s2
Una pelota de 2,8 kg resbala por un tobogán, como se observa en la figura.
Encontramos la energía potencial en el punto A y en el punto B.
Datos
m = 2,8 kg
ha = 16 m
hb = 0 m
g = 9,8 m/s2
Solución
Recordemos que la energía cinética está dada por la ecuación (2)
Despejando m, tenemos:
Finalmente reemplazamos los datos.
m = 631,1 kg
Solución
Recordemos que la energía potencial está dada por la ecuación (3).
Como los datos están en el sistema internacional, solo queda reemplazar los datos:
Comprobamos cómo se obtiene el
kilogramo. Realizamos
operaciones con las unidades.
Recordamos que el J = N m
Calculamos la energía
potencial respecto al
suelo.
Solución
Recordemos que la energía potencial está dada
por la ecuación (3)
Hallando la energía potencial en el punto A
Como los datos están en el sistema internacional, solo queda reemplazar los datos:
Hallando la energía potencial en el punto B
De igual forma solo queda reemplazar los datos en la ecuación.
Calcular la masa de un automóvil que viaja a una velocidad de 50 m/s, sabiendo
que la energía cinética que posee es 788 [J].
Datos
v = 50 m/s
Ec = 788887 [J]
Encontrar la energía potencial respecto a la mesa, del libro de 5to. de secundaria
que tiene una masa de aproximadamente 1,2 [kg].
Datos
Ep = ¿?
m = 1,2 kg
h = 2,3 m – 1.2 m = 1.1 m
g = 9,8 m/s2
Una pelota de 2,8 kg resbala por un tobogán, como se observa en la figura.
Encontramos la energía potencial en el punto A y en el punto B.
Datos
m = 2,8 kg
ha = 16 m
hb = 0 m
g = 9,8 m/s2
Solución
Recordemos que la energía cinética está dada por la ecuación (2)
Despejando m, tenemos:
Finalmente reemplazamos los datos.
m = 631,1 kg
Solución
Recordemos que la energía potencial está dada por la ecuación (3).
Como los datos están en el sistema internacional, solo queda reemplazar los datos:
Comprobamos cómo se obtiene el
kilogramo. Realizamos
operaciones con las unidades.
Recordamos que el J = N m
Calculamos la energía
potencial respecto al
suelo.
Solución
Recordemos que la energía potencial está dada
por la ecuación (3)
Hallando la energía potencial en el punto A
Como los datos están en el sistema internacional, solo queda reemplazar los datos:
Hallando la energía potencial en el punto B
De igual forma solo queda reemplazar los datos en la ecuación.
Calcular la masa de un automóvil que viaja a una velocidad de 50 m/s, sabiendo
que la energía cinética que posee es 788 [J].
Datos
v = 50 m/s
Ec = 788887 [J]
Encontrar la energía potencial respecto a la mesa, del libro de 5to. de secundaria
que tiene una masa de aproximadamente 1,2 [kg].
Datos
Ep = ¿?
m = 1,2 kg
h = 2,3 m – 1.2 m = 1.1 m
g = 9,8 m/s2
Una pelota de 2,8 kg resbala por un tobogán, como se observa en la figura.
Encontramos la energía potencial en el punto A y en el punto B.
Datos
m = 2,8 kg
ha = 16 m
hb = 0 m
g = 9,8 m/s2
Solución
Recordemos que la energía cinética está dada por la ecuación (2)
Despejando m, tenemos:
Finalmente reemplazamos los datos.
m = 631,1 kg
Solución
Recordemos que la energía potencial está dada por la ecuación (3).
Como los datos están en el sistema internacional, solo queda reemplazar los datos:
Comprobamos cómo se obtiene el
kilogramo. Realizamos
operaciones con las unidades.
Recordamos que el J = N m
Calculamos la energía
potencial respecto al
suelo.
Solución
Recordemos que la energía potencial está dada
por la ecuación (3)
Hallando la energía potencial en el punto A
Como los datos están en el sistema internacional, solo queda reemplazar los datos:
Hallando la energía potencial en el punto B
De igual forma solo queda reemplazar los datos en la ecuación.
Calcular la masa de un automóvil que viaja a una velocidad de 50 m/s, sabiendo
que la energía cinética que posee es 788 [J].
Datos
v = 50 m/s
Ec = 788887 [J]
Encontrar la energía potencial respecto a la mesa, del libro de 5to. de secundaria
que tiene una masa de aproximadamente 1,2 [kg].
Datos
Ep = ¿?
m = 1,2 kg
h = 2,3 m – 1.2 m = 1.1 m
g = 9,8 m/s2
Una pelota de 2,8 kg resbala por un tobogán, como se observa en la figura.
Encontramos la energía potencial en el punto A y en el punto B.
Datos
m = 2,8 kg
ha = 16 m
hb = 0 m
g = 9,8 m/s2
Solución
Recordemos que la energía cinética está dada por la ecuación (2)
Despejando m, tenemos:
Finalmente reemplazamos los datos.
m = 631,1 kg
Solución
Recordemos que la energía potencial está dada por la ecuación (3).
Como los datos están en el sistema internacional, solo queda reemplazar los datos:
Comprobamos cómo se obtiene el
kilogramo. Realizamos
operaciones con las unidades.
Recordamos que el J = N m
Calculamos la energía
potencial respecto al
suelo.
Solución
Recordemos que la energía potencial está dada
por la ecuación (3)
Hallando la energía potencial en el punto A
Como los datos están en el sistema internacional, solo queda reemplazar los datos:
Hallando la energía potencial en el punto B
De igual forma solo queda reemplazar los datos en la ecuación.](https://image.slidesharecdn.com/quinto-221219020539-f034d862/75/QUINTO-pdf-155-2048.jpg)
![Ministerio de Educación
SEGUNDO
TRIMESTRE
154
Calculamos la energía elástica de un resorte, cuando este se comprime 5 centímetros, sabiendo que la
constante de elasticidad es de 3.000 [N/m].
Datos
x = 5 cm ; K = 3.000 N/m ; Ec = ¿?
Solución
Convirtiendo la distancia de elongación, centímetros a metros:
Recordemos que la energía potencial elástica está dada por la ecuación (4)
Reemplazando los datos:
¿Cuál es la energía mecánica de una piedra de 10 kg que se deja
caer desde una cierta altura y alcanza una velocidad de 88 m/s,
cuando esta se encuentra a una altura de ocho metros?
Datos
h= 8 m
v = 88 m/s
m = 10 kg
g = 9,8 m/s2
Solución
Recordemos que la energía mecánica está expresada por la ecuación (5): E = Ec + Ep + Ee
En nuestro problema no se cuenta con energía elástica, por lo que la ecuación se reduce a: E = Ec + Ep
Entonces:
Reemplazando datos:
La energía es una pieza clave para entender el desarrollo de la humanidad.
El ser humano, desde el principio de su existencia, ha necesitado la energía
para sobrevivir y avanzar. Por eso podemos decir que la energía se define
como la capacidad de hacer funcionar las cosas.
Nuestros antepasados utilizaban la energía de los animales para remover
la tierra en las tareas agrícolas. Eso, también, es una forma de generar
trabajo y especialmente energía. Si bien, hoy en día, se sigue practicando
8 m](https://image.slidesharecdn.com/quinto-221219020539-f034d862/75/QUINTO-pdf-156-2048.jpg)














































































































































































































































![TERCER
TRIMESTRE
VIDA TIERRA Y TERRITORIO Química
393
Ejercicios de práctica
Ejercicios 1. a) ¿Cuántos grados aumentará el punto de ebullición del agua, si en 100 g de esta se disuelven 9 g de
glucosa?; b) ¿Cuál es la temperatura de la solución?
Respuesta: a) = 0,52
°
; b) 100,26 °C.
4. Presión osmótica
Es considerada como la cuarta propiedad coligativa que, al igual que las anteriormente estudiadas, solo depende de la
cantidad de soluto disuelto en la solución.
Esta propiedad coligativa está muy presente en la naturaleza, por lo general donde existen procesos de
intercambio de agua, nutrientes y productos de desecho provenientes del metabolismo. Algunos ejemplos
son el mecanismo de funcionamiento de los riñones y el proceso de nutrición de las plantas (subida de savia
bruta).
La presión osmótica ( ) obedece una ley muy parecida a la ley de los gases ideales:
= = ; á : = ( )
Entonces:
Agua
(disolvente
puro)
TERCER
TRIMESTRE
TERCER
TRIMESTRE
Fotoautótrofos. Son aquellos
organismos que elaboran materia
orgánica a partir de materia
inorgánica y energía solar.
)
Ósmosis invertida. Es el
proceso invertido al ósmosis,
su principal aplicación está en
la desalinización del agua.
Agua con azúcar
(solución)
Al principio se observa que los niveles de
los líquidos son iguales (condiciones
iniciales). Luego comienza el flujo de
moléculas de solvente puro, que van
desde el disolvente hacia la solución en
mayor proporción que en el sentido
inverso (desde la solución hacia el
disolvente puro).
Llega un momento de equilibrio cuando
la cantidad de moléculas de disolvente
que entran a la solución iguala a las que
salen de esta; como se observa, el
volumen de la solución aumenta y
además su concentración disminuye (se
diluye).
Esa diferencia de altura de la columna de agua
respecto a su estado inicial ejerce lo que se
conoce como presión osmótica ( ); su valor
representa la presión necesaria que debe
aplicarse a la solución para evitar el flujo de
moléculas de disolvente desde el disolvente puro
hacia la solución y viceversa (condiciones
iniciales).
=
= 62,4 = 0,082
Donde:
es el valor de la presión osmótica.
es la concentración molar de la solución.
constante universal de los gases ideales:
es la temperatura absoluta [ ]
TERCER
TRIMESTRE
Glosario
aquellos organismos
que elaboran materia
materia inorgánica y
energía solar.](https://image.slidesharecdn.com/quinto-221219020539-f034d862/75/QUINTO-pdf-395-2048.jpg)
![Ministerio de Educación
394
TERCER
TRIMESTRE
Ejercicio 1. Hallar a 18 °C la presión osmótica (en atm) de una disolución de glucosa ( ), que contiene 1 g de
soluto en 20 cm
3
de disolución.
Solución:
Datos:
= 1
= 180
= 20 = 0,02
= 18 ° = 291
Cálculos matemáticos:
=
[ ]
=
[ ]
=
1
180
0,02
= 0,28
)
= = 0,28 0,082 (291 ) = 6,63
Respuesta y explicación:
El efecto del flujo de moléculas de solvente, desde el disolvente puro hacia la solución y visceversa hasta alcanzar
el equilibrio, ocasionó una diferencia en los niveles del líquido; para lograr restituir a las condiciones iniciales se
necesitaría una presión de: = 6,63 .
Ejercicio 2. Una disolución que contiene 25 g de albúmina de huevo por litro ejerce una presión osmótica de 13,5
mmHg a 25 °C. Determinar el peso molecular de dicha proteína.
Solución:
Datos:
= 25 = 1 = 25 ° = 298
Cálculos matemáticos:
= =
=
13,5
62,4 (298 )
= 7,26 × 10
=
[ ]
= ( )( [ ])
= ( )( [ ]) =
( )( [ ])
=
25
7,26 × 10 (1 )
= 34 435,26
Respuesta y explicación:
Como se desarrolló este ejercicio, podemos concluir
que la propiedad coligativa presión osmótica nos es de
utilidad para calcular el peso molecular del soluto
disuelto.
Entonces el peso molecular de la albúmina de huevo es:
= 34 435,26 .
Ejercicios de práctica:
Ejercicios 1. a) ¿Cuántos grados aumentará el punto de ebullición del agua si en 100 g de esta se disuelven 9 g de
glucosa?; b) ¿Cuál es la temperatura de la solución?
Respuesta: a) = 0,52
°
; b) 100,26 °C.](https://image.slidesharecdn.com/quinto-221219020539-f034d862/75/QUINTO-pdf-396-2048.jpg)



























































