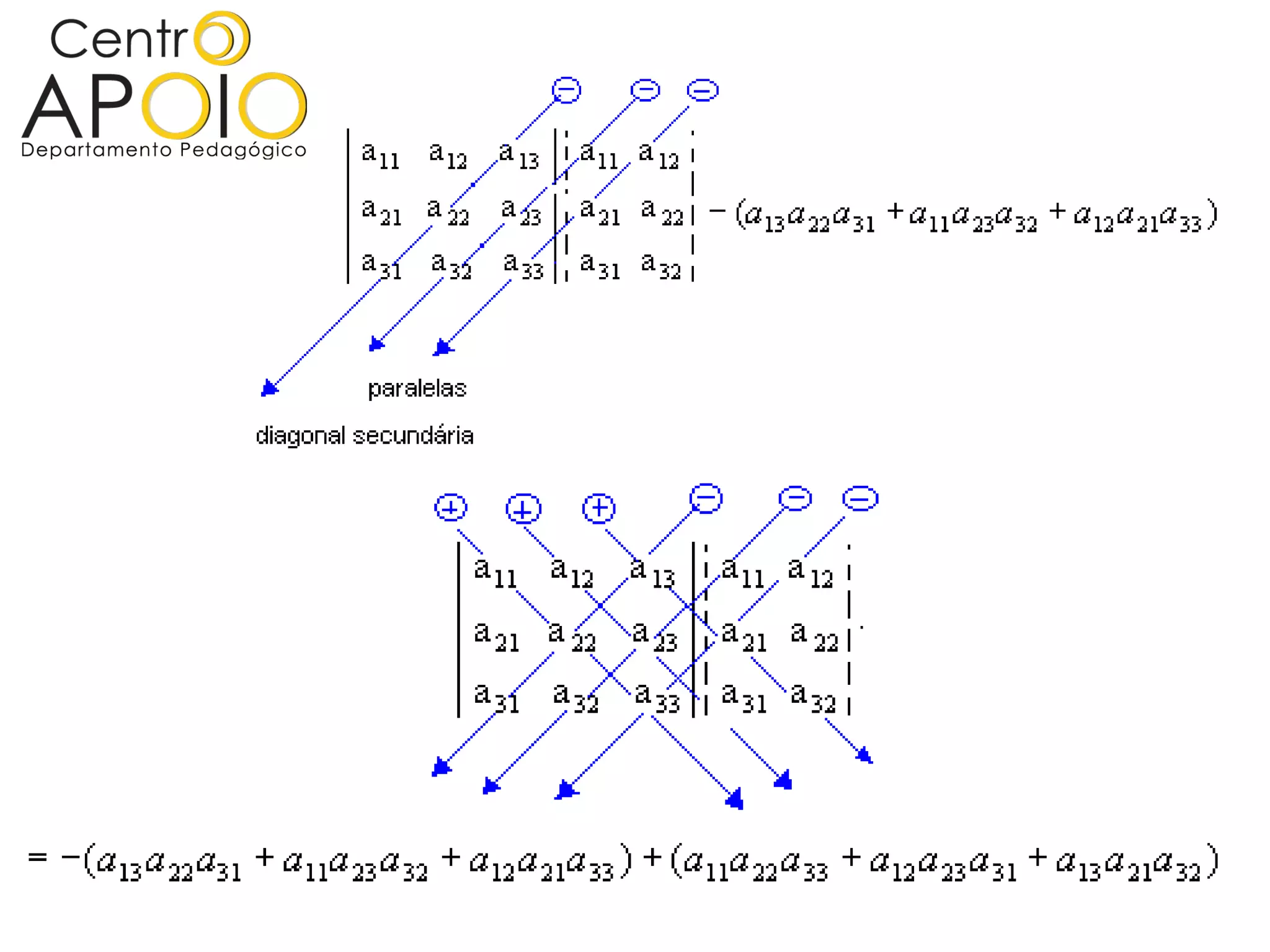
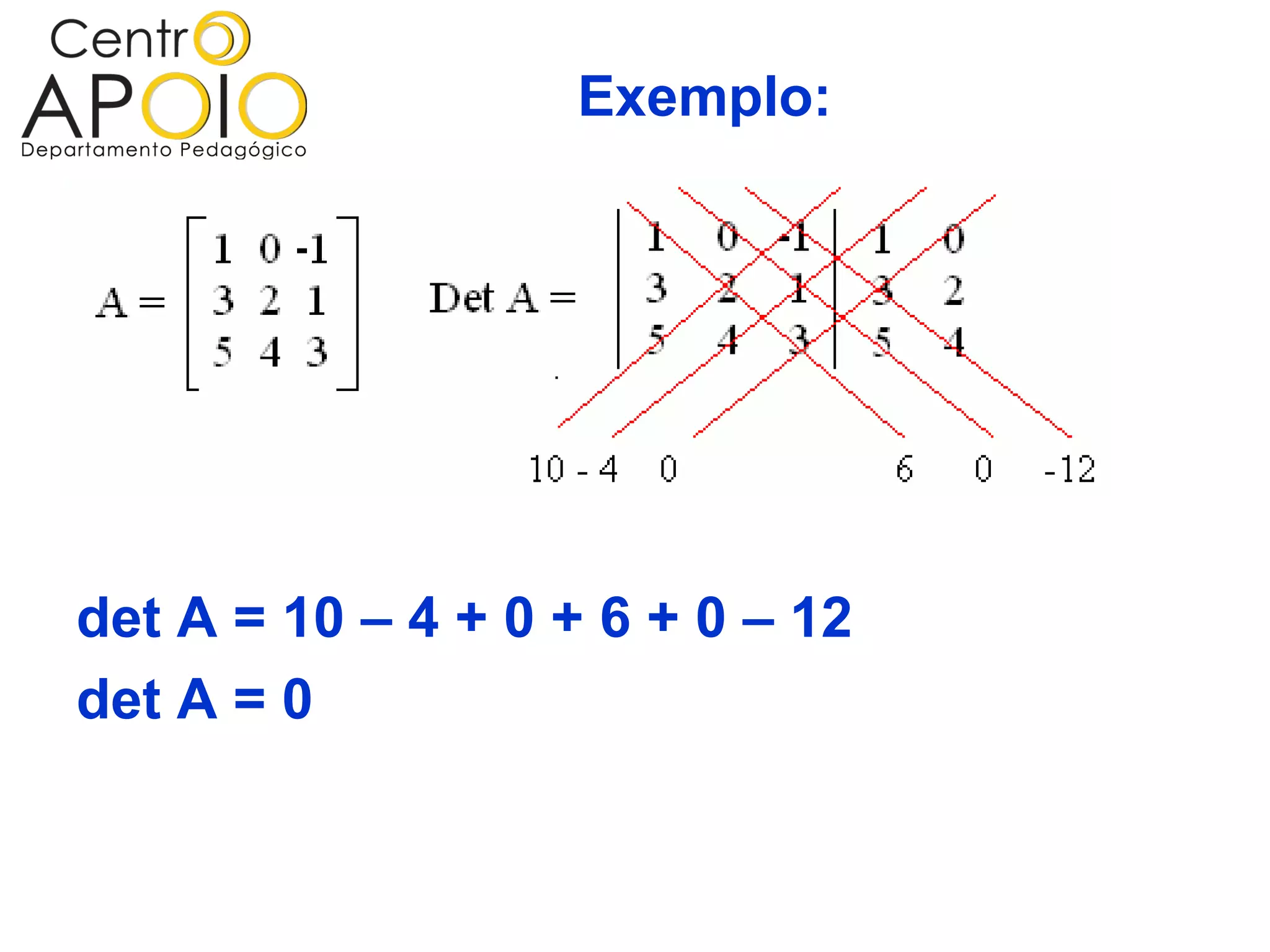
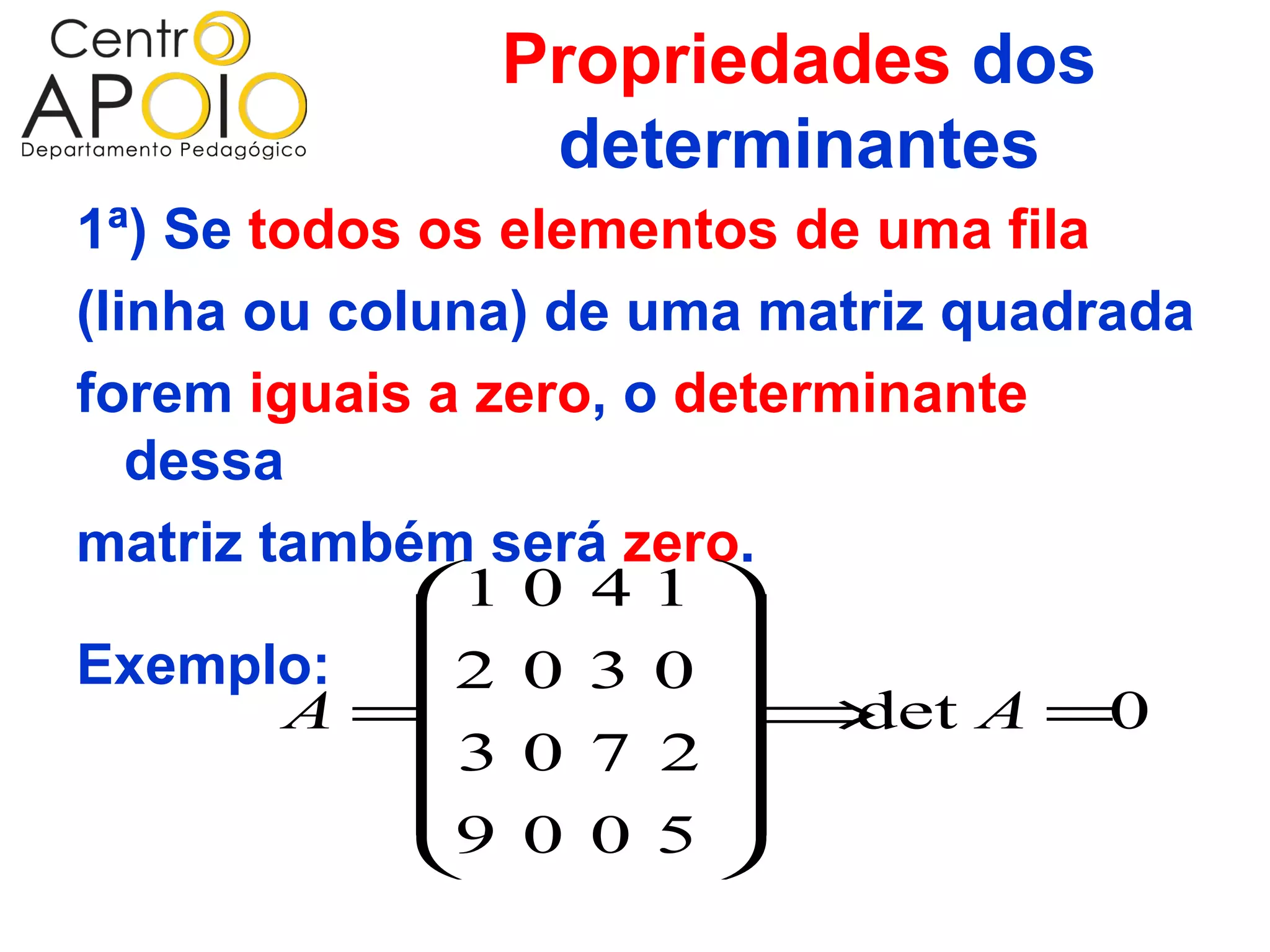
O documento explica o conceito de determinante de matrizes, incluindo como representá-lo e calculá-lo para matrizes de diferentes ordens. Ele detalha propriedades dos determinantes e apresenta o teorema de La Place para calcular determinantes de matrizes de ordem superior. Além disso, o texto fornece exemplos práticos e referências bibliográficas sobre o assunto.


























![Vamos calcular os cofator c11.
2 5 3
A = 0 − 2 −1
6 4 − 3
− 2 −1
C11 = (-1) 1+1
.
4 −3
C11 = 1.[-2 .(-3) - (-1). 4] = 6 + 4 = 10](https://image.slidesharecdn.com/determinante-120711153910-phpapp02/75/www-AulasDeMatematicaApoio-com-Matematica-Determinante-30-2048.jpg)
![Vamos calcular os cofator c23.
2 5 3
A = 0 − 2 −1
6 4 − 3
2 5
C23 = (-1) 2+3
.
6 4
C23 = -1.[2 .4 – 5 . 6] = -1. (8 - 30)= -1(-22) = 22](https://image.slidesharecdn.com/determinante-120711153910-phpapp02/75/www-AulasDeMatematicaApoio-com-Matematica-Determinante-31-2048.jpg)

![Vamos calcular o determinante
usando da segunda linha.
2 5 3
A = 0 − 2 −1
6 4 − 3
5 3
C21 = (-1) 2+1
. = -1.[5 .(-3) – 3 . 4] = 27
4 −3
2 3
C22 = (-1)2+2 . 6 − 3 = 1.[2 .(-3) - (3. 6)] = -24
2 5
C23 = (-1)2+3 . 6 4 = -1.[2 . 4 - 5. 6)] = 22](https://image.slidesharecdn.com/determinante-120711153910-phpapp02/75/www-AulasDeMatematicaApoio-com-Matematica-Determinante-33-2048.jpg)


