深入JavaScript算法世界：位运算与算法优化的20个高效策略

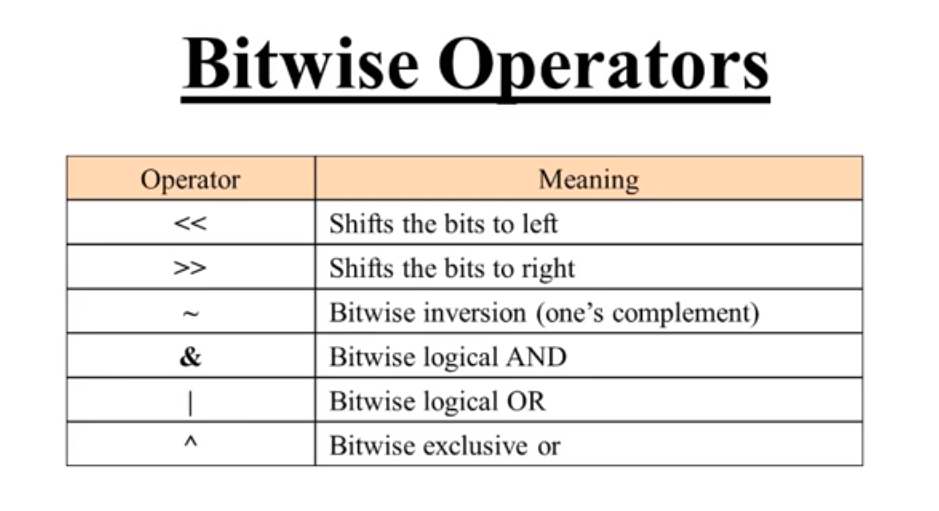
 # 1. 位运算基础与JavaScript实现 ## 位运算简介 位运算是一种在二进制层面上对数字的每一位进行运算的处理方式。它在计算机科学中占据着重要的地位，尤其是对于性能要求较高的算法和数据结构，位运算可以提供更为快速和直接的操作。 ## JavaScript中的位运算 JavaScript作为一门高级编程语言，提供了基本的位运算操作符。这些操作符包括： - `&`（与） - `|`（或） - `^`（异或） - `~`（非） - `<<`（左移） - `>>`（右移） - `>>>`（无符号右移） ## 位运算的工作原理 以 `&` 为例，它会对两个数的二进制表示进行按位比较，只有两个相应的二进制位都为1时，结果位才为1，否则为0。例如：`5 & 3`（二进制表示分别是`0101`和`0011`）的结果是 `0001`，也就是十进制中的1。 ```javascript let result = 5 & 3; // 结果为 1 ``` 在JavaScript中，位运算不仅可以用于数字操作，还可以用来处理二进制级别的操作，比如进行高速的整数运算和对内存位进行精细控制。随着对位运算的深入理解，开发者可以更好地优化代码，提高程序的执行效率。 # 2. 位运算在算法中的应用 位运算，在计算机科学中是利用二进制表示进行的运算，通常包括AND、OR、XOR、NOT、左移和右移等操作。这些运算在算法中扮演着重要角色，尤其是在性能敏感的场景下，能够显著地提高算法的效率。 ### 2.1 位运算与数学运算的转换 #### 2.1.1 位运算的基本概念 位运算直接作用于数据的二进制表示，这使得它能够以非常低的计算成本完成复杂操作。基本的位运算包括： - AND (&)：两个对应位都为1时结果为1，否则为0。 - OR (|)：两个对应位有一个为1时结果为1，否则为0。 - XOR (^)：两个对应位不同时结果为1，相同时结果为0。 - NOT (~)：单目运算符，对操作数的位进行取反操作。 - 左移 (<<)：将二进制位向左移动指定的位数，右边空出的位用0填充。 - 右移 (>>)：将二进制位向右移动指定的位数，对于有符号数，左边空出的位用符号位填充；对于无符号数，用0填充。 位运算的效率之所以高，是因为它们在硬件层面得到优化，CPU可以直接通过一系列简单的逻辑门进行计算，而不需要复杂的算术单元。 #### 2.1.2 加法与减法的位运算实现 加法运算可以通过一系列位运算和位移操作来实现。在二进制中，加法可以分解为"不进位和"和"进位和"两个部分，可以分别用 XOR 和 AND 操作来实现。例如，两个二进制数相加的步骤如下： 1. 计算不进位和：`A ^ B`（对应位置上，只要有一个为0就结果为1）。 2. 计算进位：`((A & B) << 1)`（对应位置上都为1，则产生进位）。 3. 将不进位和与进位相加，重复上述步骤直到没有进位。 减法也可以用加法来实现。要计算 A - B，可以转换为 A + (-B)。而负数在计算机中通常采用补码表示，因此，计算 `-B` 相当于对 B 的所有位取反后再加1。 ```javascript function add(a, b) { while(b != 0) { let carry = a & b; // 计算进位 a = a ^ b; // 计算不进位和 b = carry << 1; // 位移进位结果 } return a; } function subtract(a, b) { return add(a, add(~b, 1)); // 利用加法实现减法 } ``` #### 2.1.3 乘法与除法的位运算优化 乘法和除法操作通常相对加减法复杂，但是在现代CPU中，它们仍然是基本指令集的一部分。通过位运算来模拟乘法和除法的原理，可以帮助我们更好地理解这些操作，并在某些情况下用于优化。 乘法可以分解为加法的累加过程，而通过位移操作可以快速实现这个累加过程。例如，`A * 4` 只需要将 A 左移2位即可。这个原理可以用于优化乘以2的幂次的情况。 除法通常比较复杂，但可以通过反复减去除数来完成。当被除数和除数都是2的幂次时，可以通过右移操作快速完成。对于非2的幂次的情况，可以通过一系列的比较和减法操作来实现。 ### 2.2 位运算在数据结构中的应用 位运算在数据结构的应用非常广泛，尤其是在那些需要高效存储和处理大量数据的场景下，如位图算法、二进制索引树（Fenwick Tree）和布隆过滤器等。 #### 2.2.1 位图算法的应用实例 位图算法（BitMap）是一种使用位数组来表示一系列的布尔值的方法。它允许我们快速进行位运算操作，如设置值、清除值、检查是否设置值等。 位图的优点包括： - 空间效率高：相比传统的布尔数组，位图可以节省大量的存储空间。 - 访问速度快：位运算通常只需要一个CPU周期，速度快于常规的内存访问。 下面是一个简单的位图实现： ```javascript class BitMap { constructor(size) { this.size = size; this.array = new Array(Math.ceil(size / 32)); } set(index) { let byteIndex = Math.floor(index / 32); let bitIndex = index % 32; this.array[byteIndex] |= (1 << bitIndex); // 将特定位设为1 } clear(index) { let byteIndex = Math.floor(index / 32); let bitIndex = index % 32; this.array[byteIndex] &= ~(1 << bitIndex); // 将特定位设为0 } get(index) { let byteIndex = Math.floor(index / 32); let bitIndex = index % 32; return ((this.array[byteIndex] >> bitIndex) & 1) === 1; } } ``` #### 2.2.2 二进制索引树（Fenwick Tree）的实现 二进制索引树（Fenwick Tree）或称二进制索引排序树（Binary Indexed Tree），是一种数据结构，用于在可变数组上高效地计算前缀和或实现对数组元素的高效更新。 Fenwick Tree 的实现利用了位运算来找到父节点或子节点的索引，使得对树的更新操作只需要O(log n)的时间复杂度。 ```javascript class BinaryIndexedTree { constructor(size) { this.sums = new Array(size + 1); } update(index, value) { while(index < this.sums.length) { this.sums[index] += value; index += index & -index; // 位运算快速找到下一个更新的位置 } } query(index) { let sum = 0; while(index > 0) { sum += this.sums[index]; index -= index & -index; // 位运算快速找到下一个查询的位置 } return sum; } } ``` #### 2.2.3 布隆过滤器的原理与应用 布隆过滤器（Bloom Filter）是一种空间效率很高的概率型数据结构，用于判断一个元素是否在一个集合中。它由一个位数组和多个哈希函数组成，具有以下特点： - 当元素不在集合中时，布隆过滤器一定会给出“不在集合中”的结果。 - 当元素在集合中时，布隆过滤器有可能给出“不在集合中”的错误判断，称为“假阳性”。 - 不支持删除元素，一旦元素加入集合，就不能从布隆过滤器中删除。 布隆过滤器的构建需要选择合适的位数组大小和哈希函数数量，以达到希望的错误率。 ```javascript class BloomFilter { constructor(size, hashFunctions) { this.size = size; this.hashFunctions = hashFunctions; this.filter = new Array(size).fill(false); } add(item) { for(let hashFunction of this.hashFunctions) { let index = hashFunction(item) % this.size; this.filter[index] = true; } } mightContain(item) { for(let hashFunction of this.hashFunctions) { let index = hashFunction(item) % this.size; if(!this.filter[index]) return false; } return true; } } ``` ### 2.3 位运算在算法优化中的角色 位运算在算法优化中起着举足轻重的作用，尤其是在时间和空间复杂度上。合理利用位运算可以显著提升算法性能。 #### 2.3.1 时间复杂度的优化策略 时间复杂度是一个算法执行时间随输入数据增长的变化情况。通过位运算，可以以非常快的速度操作数据，从而减少算法的时间消耗。例如，在对一个数组进行遍历时，可以使用位运算快速计算下标，从而达到减少计算时间的目的。 ```javascript function processArray(arr) { for(let i = 0; i < arr.length; i++) { // 使用位运算快速计算下标 let index = (i << 1) | (i >> 1); // 仅为示例，并非实际位运算加速操作 // 处理元素 arr[index] } } ``` #### 2.3.2 空间复杂度的优化策略 空间复杂度是指在输入数据规模增长时，算法所需的存储空间量度。在一些场景下，可以通过位运算将数据压缩到更小的空间，降低空间复杂度。 ```javascript function compressData(data) { let compressed = 0; for(let bit of data) { compressed = (compressed << 1) | bit; // 将比特依次压缩进一个整数 } return compressed; } ``` #### 2.3.3 缓存友好的位运算实践 缓存友好是指算法的数据访问模式能够充分利用CPU的缓存结构，减少缓存未命中的情况，提高程序运行效率。位运算因其简单的操作，往往具有良好的缓存友好性。 ```javascript function cacheFriendlyOperation(array) { for(let i = 0; i < array.length; i += 32) { // 一次性处理32位数据，利用缓存，减少内存访问次数 let thirtyTwoBits = 0; for(let j = 0; j < 32 && (i+j) < array.length; ++j) { thirtyTwoBits |= (array[i+j] << j); } // 使用 thirtyTwoBits 进行其他操作... } } ``` 通过以上章节的详细解析，我们可以看到位运算在算法中的广泛应用和优化作用。在实际应用中，合理地运用位运算不仅可以提升程序的性能，还可以在某些特定场景中解决复杂问题。接下来的章节，我们将深入探讨位运算在JavaScript算法优化中的具体应用。 # 3. 位运算实践案例分析 ## 3.1 位运算在图算法中的应用 位运算在图算法中的应用是将复杂的图操作转化为位层面的操作，这不仅可以简化问题，而且还能显著提高算法的效率。接下来我们将详细探讨位运算在图