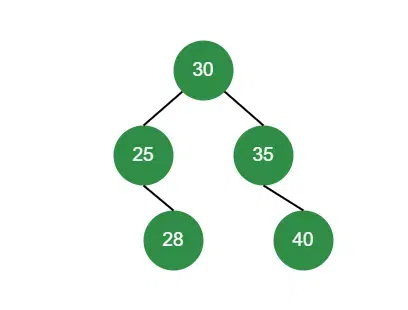
C Program for Binary Search Tree

A Binary Search Tree (BST) is a special type of binary tree that maintains its elements in a sorted order. For every node in the BST:

All nodes in its left subtree have values less than the node’s value.
All nodes in its right subtree have values greater than the node’s value.

This property ensures that each comparison allows the operation to skip about half of the remaining tree, making BST operations much faster than linear structures like arrays or linked lists.

Key Properties

Unique ordering of elements means duplicates are usually not allowed.
Inorder traversal of a BST gives sorted order of elements.
Average height: O(log n) (for balanced BST).
Worst case height: O(n) (when tree becomes skewed).

#include <stdio.h>
#include <stdlib.h>

// Define a structure for a binary tree node
struct Node
{
    int key;
    struct Node *left, *right;
};

// Function to create a new node with a given value
struct Node *newNodeCreate(int value)
{
    struct Node *temp = (struct Node *)malloc(sizeof(struct Node));
    temp->key = value;
    temp->left = temp->right = NULL;
    return temp;
}

// Function to search for a node with a specific key in the tree
struct Node *searchNode(struct Node *root, int target)
{
    if (root == NULL || root->key == target)
        return root;
    if (root->key < target)
        return searchNode(root->right, target);
    return searchNode(root->left, target);
}

// Function to insert a node with a specific value in the tree
struct Node *insertNode(struct Node *node, int value)
{
    if (node == NULL)
        return newNodeCreate(value);
    if (value < node->key)
        node->left = insertNode(node->left, value);
    else if (value > node->key)
        node->right = insertNode(node->right, value);
    return node;
}

// Function to perform post-order traversal
void postOrder(struct Node *root)
{
    if (root != NULL)
    {
        postOrder(root->left);
        postOrder(root->right);
        printf(" %d ", root->key);
    }
}

// Function to perform in-order traversal
void inOrder(struct Node *root)
{
    if (root != NULL)
    {
        inOrder(root->left);
        printf(" %d ", root->key);
        inOrder(root->right);
    }
}

// Function to perform pre-order traversal
void preOrder(struct Node *root)
{
    if (root != NULL)
    {
        printf(" %d ", root->key);
        preOrder(root->left);
        preOrder(root->right);
    }
}

// Function to find the minimum value
struct Node *findMin(struct Node *root)
{
    if (root == NULL)
        return NULL;
    else if (root->left != NULL)
        return findMin(root->left);
    return root;
}

// Function to delete a node from the tree
struct Node *delete (struct Node *root, int x)
{
    if (root == NULL)
        return NULL;
    if (x > root->key)
        root->right = delete (root->right, x);
    else if (x < root->key)
        root->left = delete (root->left, x);
    else
    {
        if (root->left == NULL && root->right == NULL)
        {
            free(root);
            return NULL;
        }
        else if (root->left == NULL || root->right == NULL)
        {
            struct Node *temp;
            if (root->left == NULL)
            {
                temp = root->right;
            }
            else
            {
                temp = root->left;
            }
            free(root);
            return temp;
        }
        else
        {
            struct Node *temp = findMin(root->right);
            root->key = temp->key;
            root->right = delete (root->right, temp->key);
        }
    }
    return root;
}

int main()
{
    // Initialize the root node
    struct Node *root = NULL;

    // Insert nodes into the binary search tree
    root = insertNode(root, 50);
    insertNode(root, 30);
    insertNode(root, 20);
    insertNode(root, 40);
    insertNode(root, 70);
    insertNode(root, 60);
    insertNode(root, 80);

    // Search for a node with key 60
    if (searchNode(root, 60) != NULL)
        printf("60 found");
    else
        printf("60 not found");

    printf("\n");

    // Perform post-order traversal
    postOrder(root);
    printf("\n");

    // Perform pre-order traversal
    preOrder(root);
    printf("\n");

    // Perform in-order traversal
    inOrder(root);
    printf("\n");

    // Perform delete the node (70)
    struct Node *temp = delete (root, 70);
    printf("After Delete: \n");
    inOrder(root);

    return 0;
}

Output

60 found
 20  40  30  60  80  70  50 
 50  30  20  40  70  60  80 
 20  30  40  50  60  70  80 
After Delete: 
 20  30  40  50  60  80

Operations

Search

Find whether a given key exists in the BST.
Time Complexity: average O(log n) and O(n) worst case

Insertion

Insert a new node while maintaining BST property.
Compare key with current node and move left/right recursively or iteratively.
Time Complexity: average O(logn) and O(n) worst case

Deletion

Remove a node while keeping BST valid.

Node has no children means remove directly.
Node has one child means replace node with its child.
Node has two children means replace node with inorder successor/predecessor and delete that successor/predecessor.
Time Complexity: average O(logn) and O(n) worst case

Traversal
The four common tree traversals are Inorder (Left, Root, Right) which gives nodes in sorted order for a BST, Preorder (Root, Left, Right), Postorder (Left, Right, Root), and Level-order, which traverses the tree level by level using a queue.

Application of Binary Search Tree

Searching and indexing (e.g., maps, sets).
Dynamic sorting and range queries.
Implementing symbol tables in compilers.
Used in advanced structures (AVL Tree, Red-Black Tree, Splay Tree).