Count of arrays having consecutive element with different values
Last Updated :
13 Sep, 2023
Given three positive integers n, k and x. The task is to count the number of different array that can be formed of size n such that each element is between 1 to k and two consecutive element are different. Also, the first and last elements of each array should be 1 and x respectively.
Examples :
Input : n = 4, k = 3, x = 2
Output : 3
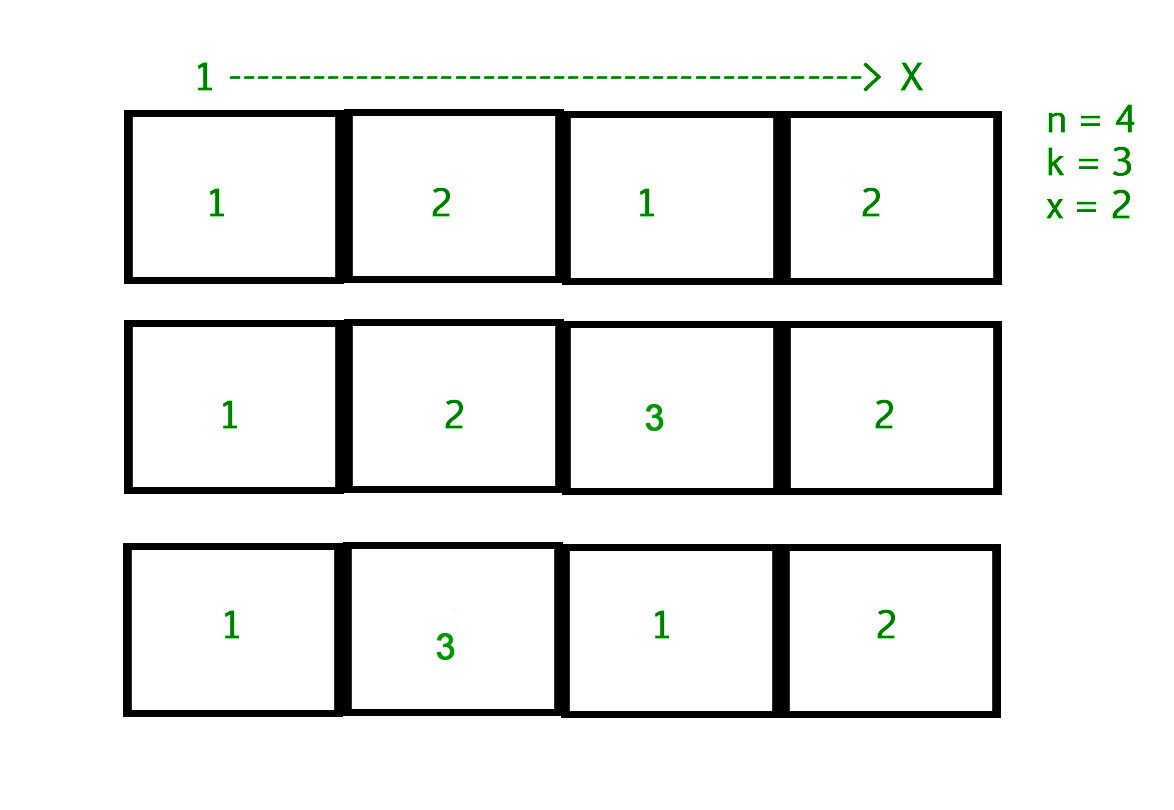
The idea is to use Dynamic Programming and combinatorics to solve the problem.
First of all, notice that the answer is same for all x from 2 to k. It can easily be proved. This will be useful later on.
Let the state f(i) denote the number of ways to fill the range [1, i] of array A such that A1 = 1 and Ai ? 1.
Therefore, if x ? 1, the answer to the problem is f(n)/(k - 1), because f(n) is the number of way where An is filled with a number from 2 to k, and the answer are equal for all such values An, so the answer for an individual value is f(n)/(k - 1).
Otherwise, if x = 1, the answer is f(n - 1), because An - 1 ? 1, and the only number we can fill An with is x = 1.
Now, the main problem is how to calculate f(i). Consider all numbers that Ai - 1 can be. We know that it must lie in [1, k].
- If Ai - 1 ? 1, then there are (k - 2)f(i - 1) ways to fill in the rest of the array, because Ai cannot be 1 or Ai - 1 (so we multiply with (k - 2)), and for the range [1, i - 1], there are, recursively, f(i - 1) ways.
- If Ai - 1 = 1, then there are (k - 1)f(i - 2) ways to fill in the rest of the array, because Ai - 1 = 1 means Ai - 2 ? 1 which means there are f(i - 2)ways to fill in the range [1, i - 2] and the only value that Ai cannot be 1, so we have (k - 1) choices for Ai.
By combining the above, we get
f(i) = (k - 1) * f(i - 2) + (k - 2) * f(i - 1)
This will help us to use dynamic programming using f(i).
Below is the implementation of this approach:
C++
// CPP Program to find count of arrays.
#include <bits/stdc++.h>
#define MAXN 109
using namespace std;
// Return the number of arrays with given constraints.
int countarray(int n, int k, int x)
{
int dp[MAXN] = { 0 };
// Initialising dp[0] and dp[1].
dp[0] = 0;
dp[1] = 1;
// Computing f(i) for each 2 <= i <= n.
for (int i = 2; i < n; i++)
dp[i] = (k - 2) * dp[i - 1] +
(k - 1) * dp[i - 2];
return (x == 1 ? (k - 1) * dp[n - 2] : dp[n - 1]);
}
// Driven Program
int main()
{
int n = 4, k = 3, x = 2;
cout << countarray(n, k, x) << endl;
return 0;
}
// Java program to find count of arrays.
import java.util.*;
class Counting
{
static int MAXN = 109;
public static int countarray(int n, int k,
int x)
{
int[] dp = new int[109];
// Initialising dp[0] and dp[1].
dp[0] = 0;
dp[1] = 1;
// Computing f(i) for each 2 <= i <= n.
for (int i = 2; i < n; i++)
dp[i] = (k - 2) * dp[i - 1] +
(k - 1) * dp[i - 2];
return (x == 1 ? (k - 1) * dp[n - 2] :
dp[n - 1]);
}
// driver code
public static void main(String[] args)
{
int n = 4, k = 3, x = 2;
System.out.println(countarray(n, k, x));
}
}
// This code is contributed by rishabh_jain
# Python3 code to find count of arrays.
# Return the number of lists with
# given constraints.
def countarray( n , k , x ):
dp = list()
# Initialising dp[0] and dp[1]
dp.append(0)
dp.append(1)
# Computing f(i) for each 2 <= i <= n.
i = 2
while i < n:
dp.append( (k - 2) * dp[i - 1] +
(k - 1) * dp[i - 2])
i = i + 1
return ( (k - 1) * dp[n - 2] if x == 1 else dp[n - 1])
# Driven code
n = 4
k = 3
x = 2
print(countarray(n, k, x))
# This code is contributed by "Sharad_Bhardwaj".
// C# program to find count of arrays.
using System;
class GFG
{
// static int MAXN = 109;
public static int countarray(int n, int k,
int x)
{
int[] dp = new int[109];
// Initialising dp[0] and dp[1].
dp[0] = 0;
dp[1] = 1;
// Computing f(i) for each 2 <= i <= n.
for (int i = 2; i < n; i++)
dp[i] = (k - 2) * dp[i - 1] +
(k - 1) * dp[i - 2];
return (x == 1 ? (k - 1) * dp[n - 2] :
dp[n - 1]);
}
// Driver code
public static void Main()
{
int n = 4, k = 3, x = 2;
Console.WriteLine(countarray(n, k, x));
}
}
// This code is contributed by vt_m
<script>
// Javascript program to find count of arrays.
let MAXN = 109;
function countarray(n, k, x)
{
let dp = [];
// Initialising dp[0] and dp[1].
dp[0] = 0;
dp[1] = 1;
// Computing f(i) for each 2 <= i <= n.
for(let i = 2; i < n; i++)
dp[i] = (k - 2) * dp[i - 1] +
(k - 1) * dp[i - 2];
return (x == 1 ? (k - 1) * dp[n - 2] :
dp[n - 1]);
}
// Driver code
let n = 4, k = 3, x = 2;
document.write(countarray(n, k, x));
// This code is contributed by sanjoy_62
</script>
<?php
// PHP Program to find
// count of arrays.
$MAXN = 109;
// Return the number of arrays
// with given constraints.
function countarray($n, $k, $x)
{
$dp = array( 0 );
// Initialising dp[0] and dp[1].
$dp[0] = 0;
$dp[1] = 1;
// Computing f(i) for
// each 2 <= i <= n.
for ( $i = 2; $i < $n; $i++)
$dp[$i] = ($k - 2) * $dp[$i - 1] +
($k - 1) * $dp[$i - 2];
return ($x == 1 ? ($k - 1) *
$dp[$n - 2] : $dp[$n - 1]);
}
// Driven Code
$n = 4; $k = 3; $x = 2;
echo countarray($n, $k, $x) ;
// This code is contributed by anuj_67.
?>
Time Complexity: O(n)
Auxiliary Space: O(MAXN), here MAXN = 109
Efficient approach: Space optimization O(1)
In the approach we have only used three variables , prev1 and prev2 to store the values of the previous two elements of the dp array and curr to store the current value. Therefore, the space complexity of the optimized code is O(1)
Implementation Steps:
- Create 2 variables prev1 and prev2 to keep track of the previous 2 values of DP and curr to store the current value.
- Initialize prev1 and prev2 with 0 and 1 as base cases.
- Now iterate through loop and get the current value form previous 2 values.
- after Every iteration assign prev2 to prev1 and curr to prev2 to iterate further;
- At last return answer.
Implementation:
C++
// CPP Program to find count of arrays.
#include <bits/stdc++.h>
#define MAXN 109
using namespace std;
// Return the number of arrays with given constraints.
int countarray(int n, int k, int x)
{
// initialize variables to store previous values
int prev1 = 0, prev2 = 1, curr;
// Computing f(i) for each 2 <= i <= n.
for (int i = 2; i < n; i++) {
curr = (k - 2) * prev2 + (k - 1) * prev1;
// assigning values to iterate further
prev1 = prev2;
prev2 = curr;
}
// return final answer
return (x == 1 ? (k - 1) * prev1 : prev2);
}
// Driven Program
int main()
{
int n = 4, k = 3, x = 2;
// function call
cout << countarray(n, k, x) << endl;
return 0;
}
import java.util.*;
public class Main {
// Return the number of arrays with given constants.
static int countArray(int n, int k, int x)
{
// initialize variables to store previous values
int prev1 = 0, prev2 = 1, curr;
// Computing f(i) for each 2 <= i <= n.
for (int i = 2; i < n; i++) {
curr = (k - 2) * prev2 + (k - 1) * prev1;
// assigning values to iterate further
prev1 = prev2;
prev2 = curr;
}
// return final answer
return (x == 1 ? (k - 1) * prev1 : prev2);
}
// Driver Program
public static void main(String[] args)
{
int n = 4, k = 3, x = 2;
// function call
System.out.println(countArray(n, k, x));
}
}
def countarray(n, k, x):
# initialize variables to store previous values
prev1 = 0
prev2 = 1
# Computing f(i) for each 2 <= i <= n.
for i in range(2, n):
curr = (k - 2) * prev2 + (k - 1) * prev1
# assigning values to iterate further
prev1 = prev2
prev2 = curr
# return final answer
return (k - 1) * prev1 if x == 1 else prev2
# Driven Program
n = 4
k = 3
x = 2
# function call
print(countarray(n, k, x))
using System;
public class Program
{
// Return the number of arrays with given constartints.
public static int CountArray(int n, int k, int x)
{
// initialize variables to store previous values
int prev1 = 0, prev2 = 1, curr;
// Computing f(i) for each 2 <= i <= n.
for (int i = 2; i < n; i++) {
curr = (k - 2) * prev2 + (k - 1) * prev1;
// assigning values to iterate further
prev1 = prev2;
prev2 = curr;
}
// return final answer
return (x == 1 ? (k - 1) * prev1 : prev2);
}
// Driven Program
public static void Main()
{
int n = 4, k = 3, x = 2;
// function call
Console.WriteLine(CountArray(n, k, x));
}
}
// Function to calculate the number of arrays with given constants.
function countArray(n, k, x) {
let prev1 = 0, prev2 = 1, curr;
// Computing f(i) for each 2 <= i < n.
for (let i = 2; i < n; i++) {
// Calculate the current value using the given formula.
curr = (k - 2) * prev2 + (k - 1) * prev1;
// Update the previous values for the next iteration.
prev1 = prev2;
prev2 = curr;
}
// Return the final answer based on the value of x.
return (x === 1 ? (k - 1) * prev1 : prev2);
}
// Input values
let n = 4, k = 3, x = 2;
// Calculate and output the result
console.log(countArray(n, k, x));
Time Complexity: O(n)
Auxiliary Space: O(1)
Similar Reads
DSA Tutorial - Learn Data Structures and Algorithms DSA (Data Structures and Algorithms) is the study of organizing data efficiently using data structures like arrays, stacks, and trees, paired with step-by-step procedures (or algorithms) to solve problems effectively. Data structures manage how data is stored and accessed, while algorithms focus on
7 min read
Quick Sort QuickSort is a sorting algorithm based on the Divide and Conquer that picks an element as a pivot and partitions the given array around the picked pivot by placing the pivot in its correct position in the sorted array. It works on the principle of divide and conquer, breaking down the problem into s
12 min read
Merge Sort - Data Structure and Algorithms Tutorials Merge sort is a popular sorting algorithm known for its efficiency and stability. It follows the divide-and-conquer approach. It works by recursively dividing the input array into two halves, recursively sorting the two halves and finally merging them back together to obtain the sorted array. Merge
14 min read
Bubble Sort Algorithm Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in the wrong order. This algorithm is not suitable for large data sets as its average and worst-case time complexity are quite high.We sort the array using multiple passes. After the fir
8 min read
Data Structures Tutorial Data structures are the fundamental building blocks of computer programming. They define how data is organized, stored, and manipulated within a program. Understanding data structures is very important for developing efficient and effective algorithms. What is Data Structure?A data structure is a st
2 min read
Breadth First Search or BFS for a Graph Given a undirected graph represented by an adjacency list adj, where each adj[i] represents the list of vertices connected to vertex i. Perform a Breadth First Search (BFS) traversal starting from vertex 0, visiting vertices from left to right according to the adjacency list, and return a list conta
15+ min read
Binary Search Algorithm - Iterative and Recursive Implementation Binary Search Algorithm is a searching algorithm used in a sorted array by repeatedly dividing the search interval in half. The idea of binary search is to use the information that the array is sorted and reduce the time complexity to O(log N). Binary Search AlgorithmConditions to apply Binary Searc
15 min read
Insertion Sort Algorithm Insertion sort is a simple sorting algorithm that works by iteratively inserting each element of an unsorted list into its correct position in a sorted portion of the list. It is like sorting playing cards in your hands. You split the cards into two groups: the sorted cards and the unsorted cards. T
9 min read
Dijkstra's Algorithm to find Shortest Paths from a Source to all Given a weighted undirected graph represented as an edge list and a source vertex src, find the shortest path distances from the source vertex to all other vertices in the graph. The graph contains V vertices, numbered from 0 to V - 1.Note: The given graph does not contain any negative edge. Example
12 min read
Selection Sort Selection Sort is a comparison-based sorting algorithm. It sorts an array by repeatedly selecting the smallest (or largest) element from the unsorted portion and swapping it with the first unsorted element. This process continues until the entire array is sorted.First we find the smallest element an
8 min read