Orthogonal Linked List

An Orthogonal Linked List is a data structure composed of fundamental elements called Nodes (similar to linked lists). Each node in an orthogonal Linked List points to 4 other nodes, namely up, down, left and right. In essence, just like a matrix is a 2D version of an array, an orthogonal linked list is a 2D version of a linear linked list. 

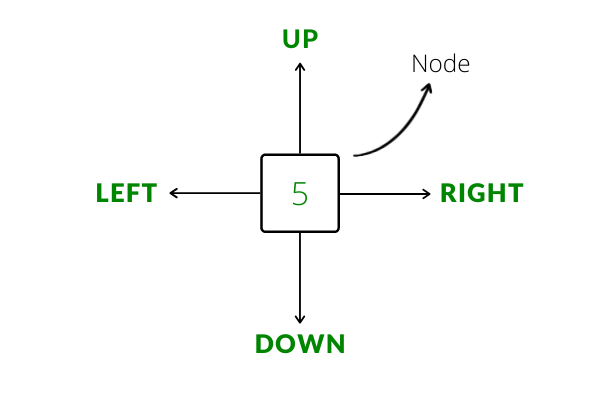
Algorithm to convert a matrix into an Orthogonal Linked List :

1. Create a node for each cell in the matrix. In a map, and also store the value of the cell and a pointer to the created node for the cell.
2. If the current row (i) is not the 0th row of the matrix, set the current node's up pointer to the node of the cell just above it (use the map to get the correct pointer) and set the node above's down pointer to the current node. 
3. Similarly, if the current column (j) is not the 0the column of the matrix, set the current node's left pointer to the node of the cell to the left of the current node and set the node to the left's right pointer to the current node
4. repeat process 1 to 3 for every cell in the matrix
5. return map[(matrix[0][0])] to return the pointer to the top-left node of the orthogonal linked list

Below is an implementation of the algorithm above.

Input:
    matrix = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9}
    }

Output: 
    A Node pointing to the top-left corner of the orthogonal linked list.
    
       ^      ^      ^
       |      |      |
    <--1 <--> 2 <--> 3-->
       ^      ^      ^
       |      |      |
       v      v      v
    <--4 <--> 5 <--> 6-->
       ^      ^      ^
       |      |      |
       v      v      v
    <--7 <--> 8 <--> 9-->
       |      |      |
       v      v      v

#include <bits/stdc++.h>
using namespace std;

struct MatrixNode
{
    int _val;
    MatrixNode* _u; // pointer to node above
    MatrixNode* _d; // pointer to node below
    MatrixNode* _l; // pointer to node towards left
    MatrixNode* _r; // pointer to node towards right

    // Constructor for MatrixNode
    MatrixNode( int val = 0, 
                MatrixNode* u = nullptr,
                MatrixNode* d = nullptr,
                MatrixNode* l = nullptr,
                MatrixNode* r = nullptr )
        {
            _val = val;
            _u = u;
            _d = d;
            _l = l;
            _r = r;
        }
};

MatrixNode* BuildOrthogonalList(int matrix[][3], int r, int c)
{
    // an unordered_map to store the {value, pointers} pair
    // for easy access while building the list
    unordered_map<int, MatrixNode*> mp;

    for(int i = 0; i < r; i++)
    {
        for(int j = 0; j < c; j++)
        {
            // create a newNode for each entry in the matrix
            MatrixNode* newNode = new MatrixNode(matrix[i][j]);
            // store the pointer of the new node
            mp[(matrix[i][j])] = newNode; 

            // set the up and down pointing pointers correctly
            if(i != 0)
            {
                newNode->_u = mp[(matrix[i - 1][j])];
                mp[(matrix[i - 1][j])]->_d = newNode;
            }

            // similarly set the left and right pointing pointers
            if(j != 0)
            {
                newNode->_l = mp[(matrix[i][j - 1])];
                mp[(matrix[i][j - 1])]->_r = newNode;
            }
        }
    }

    // return the start of the list
    return mp[(matrix[0][0])];
}

void PrintOrthogonalList(MatrixNode* head)
{
    MatrixNode* curRow; // will point to the begin of each row
    MatrixNode* cur; // will traverse each row and print the element
    for(curRow = head; curRow != nullptr; curRow = curRow->_d)
    {
        for(cur = curRow; cur != nullptr; cur = cur->_r)
        {
            cout << cur->_val << " ";
        }
        cout << endl;
    }
}

int main()
{
    int matrix[3][3] = {
        {1, 2, 3},
        {4, 5, 6},
        {7, 8, 9}
    };

    MatrixNode* list = BuildOrthogonalList(matrix, 3, 3);
    PrintOrthogonalList(list);

    return 0;
}

// Java code for the above approach
import java.io.*;
import java.util.*;

class MatrixNode {
  int val;
  MatrixNode u, d, l, r;

  MatrixNode(int val) { this.val = val; }
}

class GFG {

  static MatrixNode buildOrthogonalList(int[][] matrix,
                                        int r, int c)
  {
    // a map to store the {value, pointers} pair for
    // easy access
    Map<Integer, MatrixNode> mp = new HashMap<>();

    for (int i = 0; i < r; i++) {
      for (int j = 0; j < c; j++) {
        // create a newNode for each entry in the
        // matrix
        MatrixNode newNode
          = new MatrixNode(matrix[i][j]);
        // store the pointer of the new node
        mp.put(matrix[i][j], newNode);

        // set the up and down pointing pointers
        // correctly
        if (i != 0) {
          newNode.u = mp.get(matrix[i - 1][j]);
          mp.get(matrix[i - 1][j]).d = newNode;
        }

        // similarly set the left and right pointing
        // pointers
        if (j != 0) {
          newNode.l = mp.get(matrix[i][j - 1]);
          mp.get(matrix[i][j - 1]).r = newNode;
        }
      }
    }

    // return the start of the list
    return mp.get(matrix[0][0]);
  }

  public static void printOrthogonalList(MatrixNode head)
  {
    MatrixNode curRow
      = head; // will point to the begin of each row
    MatrixNode cur = null; // will traverse each row and
    // print the element
    while (curRow != null) {
      cur = curRow;
      while (cur != null) {
        System.out.print(cur.val + " ");
        cur = cur.r;
      }
      System.out.println();
      curRow = curRow.d;
    }
  }

  public static void main(String[] args)
  {
    int[][] matrix
      = { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } };

    MatrixNode list = buildOrthogonalList(matrix, 3, 3);
    printOrthogonalList(list);
  }
}

// This code is contributed by lokeshmvs21.

# Python code for the above approach
class MatrixNode:
    def __init__(self, val = 0, u = None, d = None, l = None, r = None):
        self._val = val
        self._u = u
        self._d = d
        self._l = l
        self._r = r

def BuildOrthogonalList(matrix, r, c):
    """
    Builds an orthogonal list from a given matrix
    """
    # a dictionary to store the {value, pointers} pair
    # for easy access while building the list
    mp = {}

    for i in range(r):
        for j in range(c):
            # create a newNode for each entry in the matrix
            newNode = MatrixNode(matrix[i][j])
            # store the pointer of the new node
            mp[(matrix[i][j])] = newNode

            # set the up and down pointing pointers correctly
            if i != 0:
                newNode._u = mp[(matrix[i - 1][j])]
                mp[(matrix[i - 1][j])]._d = newNode

            # similarly set the left and right pointing pointers
            if j != 0:
                newNode._l = mp[(matrix[i][j - 1])]
                mp[(matrix[i][j - 1])]._r = newNode

    # return the start of the list
    return mp[(matrix[0][0])]

def PrintOrthogonalList(head):
    """
    Prints the given orthogonal list
    """
    curRow = head # will point to the begin of each row
    cur = None # will traverse each row and print the element
    while curRow:
        cur = curRow
        while cur:
            print(cur._val, end=" ")
            cur = cur._r
        print()
        curRow = curRow._d

matrix = [
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
]

list = BuildOrthogonalList(matrix, 3, 3)
PrintOrthogonalList(list)

# This code is contributed by lokeshpotta20.

// C# code equivalent to the Java code
using System;
using System.Collections.Generic;

class MatrixNode
{
  public int val;
  public MatrixNode u, d, l, r;

  public MatrixNode(int val)
  {
    this.val = val;
  }
}

class Program
{
  static MatrixNode buildOrthogonalList(int[,] matrix, int r, int c)
  {
    // a dictionary to store the {value, pointers} pair for easy access
    Dictionary<int, MatrixNode> mp = new Dictionary<int, MatrixNode>();

    for (int i = 0; i < r; i++)
    {
      for (int j = 0; j < c; j++)
      {
        // create a newNode for each entry in the matrix
        MatrixNode newNode = new MatrixNode(matrix[i, j]);
        // store the pointer of the new node
        mp[(matrix[i, j])] = newNode;

        // set the up and down pointing pointers correctly
        if (i != 0)
        {
          newNode.u = mp[(matrix[i - 1, j])];
          mp[(matrix[i - 1, j])].d = newNode;
        }

        // similarly set the left and right pointing pointers
        if (j != 0)
        {
          newNode.l = mp[(matrix[i, j - 1])];
          mp[(matrix[i, j - 1])].r = newNode;
        }
      }
    }

    // return the start of the list
    return mp[(matrix[0, 0])];
  }

  public static void printOrthogonalList(MatrixNode head)
  {
    MatrixNode curRow = head; // will point to the begin of each row
    MatrixNode cur = null; // will traverse each row and print the element
    while (curRow != null)
    {
      cur = curRow;
      while (cur != null)
      {
        Console.Write(cur.val + " ");
        cur = cur.r;
      }
      Console.WriteLine();
      curRow = curRow.d;
    }
  }

  static void Main(string[] args)
  {
    int[,] matrix = { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } };

    MatrixNode list = buildOrthogonalList(matrix, 3, 3);
    printOrthogonalList(list);
  }
}

// JavaScript code for the above approach

class MatrixNode {
  constructor(val) {
    this.val = val;
    this.u = null;
    this.d = null;
    this.l = null;
    this.r = null;
  }
}

function buildOrthogonalList(matrix, r, c) {
  // a map to store the {value, pointers} pair of easy access
  const mp = new Map();

  for (let i = 0; i < r; i++) {
    for (let j = 0; j < c; j++) {
      // create a newNode for each entry in the matrix
      const newNode = new MatrixNode(matrix[i][j]);
      
      // store the pointer of the new Node
      mp.set(matrix[i][j], newNode);

      // set the up and down pointing pointers correctly
      if (i !== 0) {
        newNode.u = mp.get(matrix[i - 1][j]);
        mp.get(matrix[i - 1][j]).d = newNode;
      }

      // similarly set the left and right pointing pointers
      if (j !== 0) {
        newNode.l = mp.get(matrix[i][j - 1]);
        mp.get(matrix[i][j - 1]).r = newNode;
      }
    }
  }

  // return the start of the list
  return mp.get(matrix[0][0]);
}

function printOrthogonalList(head) {
  let curRow = head; // will point to the begin of each row
  let cur = null;  // will traverse each row and print the element
  while (curRow !== null) {
    cur = curRow;
    while (cur !== null) {
      console.log(cur.val + " ");
      cur = cur.r;
    }
    console.log("<br>");
    curRow = curRow.d;
  }
}

const matrix = [
  [1, 2, 3],
  [4, 5, 6],
  [7, 8, 9]
];

const list = buildOrthogonalList(matrix, 3, 3);
printOrthogonalList(list);

// This code is contributed by sankar.

Application:
The most common application of orthogonal linked list is in sparse matrix representation. In brief, a sparse matrix is a matrix in which most of its elements are zeroes (or any known constant). They appear often in scientific applications. Representing sparse matrices as a 2D array is a huge wastage of memory. Instead, sparse matrices are represented as an orthogonal linked list. We create a node only for non-zero elements in the matrix and in each node, we store the value, the row index and the column index along with the necessary pointers to other nodes. This saves a lot of performance overhead and is the most memory-efficient way to implement a sparse matrix.

ayush.verma16

Follow

Improve

Article Tags :

• Linked List
• GATE CS
• DSA
• Linked Lists
• Data Structures

+1 More

Practice Tags :

• Data Structures
• Linked List