Last Minute Notes - Theory of Computation
Last Updated :
24 Jan, 2025
The Theory of Computation (TOC) is a critical subject in the GATE Computer Science syllabus. It involves concepts like Finite Automata, Regular Expressions, Context-Free Grammars, and Turing Machines, which form the foundation of understanding computational problems and algorithms.
This article provides Last Minute Notes for TOC, focusing on the most important topics that are frequently asked in GATE.
Basics
1. Symbol and Alphabet
- Symbol: A single character or entity, e.g.,
a, b, 1, 0. - Alphabet (Σ): A finite set of symbols, e.g.,
Σ = {a, b}.
2. String
- String: A finite sequence of symbols from an alphabet, e.g.,
abba. - Empty String (ε): A string with no symbols.
3. Operations on Strings
- Concatenation: Joining two strings.
Example: w1 = ab, w2 = ba → w1.w2 = abba. - Length (|w|): Number of symbols in a string.
Example: |abba| = 4. - Reverse (w^R): Reversing the order of symbols.
Example: w = abba → w^R = abba.
4. Prefix, Suffix, and Substring
- Prefix: Any leading part of a string.
Example: For w = abba, prefixes are {ε, a, ab, abb, abba}. - Suffix: Any trailing part of a string.
Example: For w = abba, suffixes are {ε, a, ba, bba, abba}. - Substring: Any continuous part of a string.
Example: For w = abba, substrings are {ε, a, b, ab, ba, bb, abb, bba, abba}.
5. Language
- Language (L): A set of strings over an alphabet.
Example: L = {w ∈ Σ* | w starts with a and ends with b}.
For Σ = {a, b}, L = {ab, aab, abb, ...}.
Types of Languages
• Finite Language • Infinite Language • Regular language • DCFL (Deterministic CFL) • CFL • CSL • Recursive Language • Recursive Enumerable Language (REL)

Relation Between Symbol, Alphabet, String, and Language
- Symbol: The smallest unit, e.g.,
a, b, 0, 1. - Alphabet (Σ): A finite set of symbols, e.g.,
Σ = {a, b}. - String: A sequence of symbols from an alphabet, e.g.,
abba. - Language: A set of strings over an alphabet, e.g.,
L = {ab, aab, abb}.
Chomsky Hierarchy
 Chomsky Hierarchy
Chomsky HierarchyRead more about Chomsky Hierarchy in TOC.
Finite Automata
Finite Automata (FA) is a simple mathematical model used to represent and recognize regular languages. FA = (Q, Σ, δ, q0 , F)
Finite Automaton can be categorized into two types:
Acceptor (Without Output)
- DFA (Deterministic Finite Automaton)
- NFA (Non-Deterministic Finite Automaton)
Transducer (With Output)
- Moore Machine
- Mealy Machine
Types of FA:
- Deterministic Finite Automata (DFA): Transition function: δ: Q × Σ → Q
(Maps a state and input symbol to a single next state). - Non-Deterministic Finite Automata (NFA):
- Without ε-moves: δ: Q × Σ → 2^Q
(Maps a state and input symbol to a set of possible states). - With ε-moves: δ: Q × (Σ ∪ {ε}) → 2^Q
(Maps a state and input symbol or ε to a set of possible states).
Read more about Introduction to FA.
Note:
- Language accepted by NDFA and DFA are same.
- Power of NDFA and DFA is same.
- No. of states in NDFA is less than or equal to no. of states in equivalent DFA.
- For NFA with n-states, in worst case, the maximum states possible in DFA is 2n
- Every NFA can be converted to corresponding DFA.
Steps to Construct a DFA:
- Identify the input alphabet (Σ) and the states (Q).
- Define the initial state and the final states.
- Create a transition table or diagram ensuring every input symbol from each state leads to exactly one state.
- Ensure the DFA accepts all strings of the given language and rejects others.
Steps to Construct an NFA:
- Identify the pattern or condition the NFA should accept.
- Create states for each stage of processing the input.
- Start from an initial state.
- Define one or more final states based on acceptance criteria.
- Allow multiple transitions for the same input symbol.
- Include ε-transitions if needed (moves without consuming input).
- Check if it accepts all strings in the language and rejects others.
Simple and flexible, NFAs are easier to design than DFAs.
NFA to DFA Conversion
Step 1: Convert the given NFA to its equivalent transition table.
Step 2: Create the DFA’s start state.
Step 3: Create the DFA’s transition table.
Step 4: Create the DFA’s final states.
Step 5: Simplify the DFA.
Step 6: Repeat steps 3-5 until no further simplification is possible.
Read more about NFA to DFA Conversion, Here.
Minimization of DFA
Suppose there is a DFA D < Q, Δ, q0, Δ, F > which recognizes a language L. Then the minimized DFA D < Q’, Δ, q0, Δ, F’ > can be constructed for language L as:
Step 1: We will divide Q (set of states) into two sets. One set will contain all final states and other set will contain non-final states. This partition is called P0.
Step 2: Initialize k = 1
Step 3: Find Pk by partitioning the different sets of Pk-1. In each set of Pk-1, we will take all possible pair of states. If two states of a set are distinguishable, we will split the sets into different sets in Pk.
Step 4: Stop when Pk = Pk-1 (No change in partition)
Step 5: All states of one set are merged into one. No. of states in minimized DFA will be equal to no. of sets in Pk.
How to find whether two states in partition Pk are distinguishable ?
Two states ( qi, qj ) are distinguishable in partition Pk if for any input symbol a, Δ ( qi, a ) and Δ ( qj, a ) are in different sets in partition Pk-1.
Read more about Minimization of DFA.
Moore and Mealy Machine
Moore Machine:
- Output depends on the state only.
- Output is produced when entering a state.
- Example: Output =
{q0 → 0, q1 → 1}. - Representation: M=(Q,Σ,Δ,δ,λ,q0) Where λ is the output function.
Mealy Machine:
- Output depends on the state and input.
- Output is produced during transitions.
- Example: Transition
q0 → q1 on a produces 1. - Representation: M=(Q,Σ,Δ,δ,λ,q0) Where λ is the transition-based output function.
Note: Mealy Machines often require fewer states than Moore Machines for the same functionality.
Read about Mealy and Moore Machine, Here.
Regular Expression
A regular expression represents a regular language and describes a regular set.
Operators of Regular Expressions
OR (|): Binary Operator, Combines two patterns, Example: a|b → {a, b}.
Concatenation (.): Binary Operator, Joins two patterns in sequence, Example: ab → {ab}.
Kleene Star (*): Unary Operator, Allows repetition (zero or more times), Example: a* → {ε, a, aa, aaa, ...}.
Kleene Plus (+): Unary Operator, Allows repetition (one or more times), Example: a+ → {a, aa, aaa, ...}.
Language Over Σ
Languages over an alphabet (Σ) can be classified as:
Finite Set:
- Always a Regular Language.
Infinite Set:
- L Over |Σ| = 1:
- If it forms an Arithmetic Progression (AP) → Regular Language.
- If it does not form an AP → Non-Regular.
- L Over |Σ| > 1:
- Can be either a Regular Language or a Non-Regular Language, depending on the conditions.
Identification of Regular Languages
1. Finite Languages are Always Regular
2. Infinite Languages are Regular if they Follow Patterns
- Infinite languages are regular if they can be expressed with a finite automaton or a regular expression.
- Example:
L = {a^n | n ≥ 0} (Strings with any number of as) → Regular, as it can be represented by a DFA with loops.L = {a^n b^m | n, m ≥ 0} → Regular because it doesn’t require memory to match n with m.
3. Closure Properties of Regular Languages
- Regular languages are not closed under subset operation and the six infinite operations because these operations often require memory, context, or infinite processing, which finite automata lack.
- Finite operations, like union, concatenation, and intersection (over finite languages), are closed because they can be managed within the scope of finite automata.
Read about Closure Properties of Regular Languages, Here.
4. How to Identify Non-Regular Languages
A language is not regular if:
- Memory is required: The language needs to keep track of counts or comparisons.
Example: L = {a^n b^n | n ≥ 0} → Non-regular, as it requires matching the number of as and bs. - Nested Patterns: The language contains self-referencing structures like palindromes.
Example: L = {ww^R | w ∈ Σ*} → Non-regular.
5. Pumping Lemma Test
- Purpose: To prove that a language is not regular.
- Statement: For any regular language
L, there exists a pumping length p such that any string w in L with |w| ≥ p can be split into xyz where: xy^iz ∈ L for all i ≥ 0.|y| > 0.|xy| ≤ p.
Read about Properties of RegEx, Here.
Arden's Theorem
Statement:
- Arden's Theorem provides a method to solve regular expression equations of the form:
R=Q+RP, where R,Q,P are regular expressions.
Solution:
- The solution for R is:
R=QP^*if P does not contain ε (epsilon).
Example:
Given R=a+Rb:
- Using Arden's Theorem: R = a(b^*).
Read about Arden's Theorem, Here.
Regular Grammar
Definition: A regular grammar is a formal grammar that generates regular languages.
Types of Regular Grammar:
- Right-Linear Grammar:
Productions are of the form:
A→aB or A→a, where A,B are non-terminals and a is a terminal. - Left-Linear Grammar:
Productions are of the form:
A→Ba or A→a.
Properties:
- Regular grammars correspond to finite automata.
- Right-linear grammars are used for DFA/NFA construction.
Example :
Grammar :
Language (L): L={aa,bb}
- Regular languages generated from grammars are calculated bottom-to-top (from the base rules upward).
- Use substitution to derive the final language.
Read about Regular Grammar, Here.
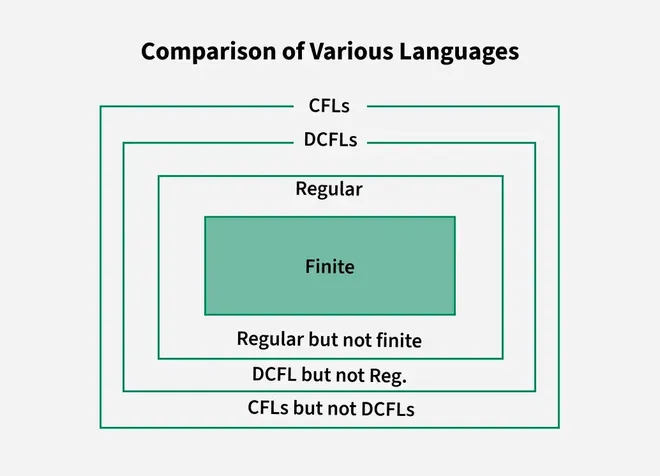
Push Down Automata
Context Free Grammar
Definition: A context-free language is generated by a Context-Free Grammar (CFG) where each production rule follows:
V → (V ∪ T)*
- LHS (Left-Hand Side): Only one variable (non-terminal).
- RHS (Right-Hand Side): A combination of terminals and/or non-terminals.
Derivations to Generate Strings:
- Linear Derivation:
(a) Left Most Derivation (LMD): Expand the leftmost variable first.
(b) Right Most Derivation (RMD): Expand the rightmost variable first. - Non-Linear Derivation:
- Also called Parse Tree or Derivation Tree.
- Represents a hierarchical structure of derivation.
Types of Context-Free Grammars (CFG)
Ambiguous Grammar:
- A CFG is ambiguous if a string has more than one parse tree or derivation.
- Example: S→SS∣a.
Unambiguous Grammar:
- A CFG is unambiguous if every string has exactly one parse tree or derivation.
Left-Recursive Grammar:
- A grammar is left-recursive if a production rule has the form A→Aα, where α is a string.
- Example: S→Sa∣b.
Right-Recursive Grammar:
- A grammar is right-recursive if a production rule has the form A→αA, where α is a string.
- Example: S→aS∣b.
Regular Grammar:
- A special type of CFG where rules are either right-linear or left-linear.
Read about Context Free Grammar, Here.
PDA
A PDA is a computational model that extends a finite automaton by using a stack for additional memory. It recognizes context-free languages (CFLs).
Read about Introduction to Pushdown Automata, Here.
Types of Pushdown Automata (PDA)
Pushdown Automata (PDA) are used to recognize context-free languages (CFLs), classified into deterministic context-free languages (DCFLs) and general CFLs.
1. Deterministic Pushdown Automata (DPDA)
- Definition: A DPDA allows at most one transition for each combination of input symbol, current state, and stack symbol.
- Recognizes: Deterministic Context-Free Languages (DCFLs), which are a subset of CFLs.
- Characteristics:
- Cannot handle ambiguity (e.g., ambiguous grammars).
- Requires deterministic parsing.
- Example language: L = \{a^n b^n | n \geq 0\} (balanced strings).
- Usage:
- Recognizes languages with clear, unambiguous structures.
2. Non-Deterministic Pushdown Automata (NPDA)
- Definition: An NPDA allows multiple transitions for the same input symbol, current state, and stack symbol.
- Recognizes: All Context-Free Languages (CFLs).
- Characteristics:
- Can handle ambiguity (e.g., ambiguous grammars).
- Example language: L = \{a^n b^m c^n | n, m \geq 0\}.
- Supports more complex structures than DPDAs.
- Usage:
- Recognizes all CFLs, including ambiguous languages.
Note:
- Power of NPDA is more than DPDA.
- It is not possible to convert every NPDA to corresponding DPDA.
- Language accepted by DPDA is subset of language accepted by NPDA.
- The languages accepted by DPDA are called DCFL (Deterministic Context Free Languages) which are subset of NCFL (Non Deterministic CFL) accepted by NPDA.
Key Difference Between DPDA and NPDA
| Feature | DPDA | NPDA |
|---|
| Language Recognized | DCFL (Subset of CFL) | CFL (All Context-Free Languages) |
| Transitions | Single transition per input | Multiple transitions allowed |
| Ambiguity | Cannot handle ambiguous grammars | Can handle ambiguous grammars |
Read about Difference Between DPDA and NPDA, Here.
Closure Properties of CFLs and DCFLs
| Operation | CFL | DCFL |
|---|
| Union (L1∪L2) | Closed | Not Closed |
| Concatenation (L1⋅L2) | Closed | Not Closed |
| Kleene Star (L*) | Closed | Not Closed |
| Intersection (L1∩L2) | Not Closed | Closed with Regular |
| Complement (Lc) | Not Closed | Closed |
| Reversal (LR) | Closed | Not Closed |
| Homomorphism | Closed | Not Closed |
| Substitution | Closed | Not Closed |
| Intersection with Regular | Closed | Closed |
| Difference (L1−L2) | Not Closed | Not Closed |
Read about Closure Properties of CFLs, Here.

Key Points:
- DCFL ∪ Regular = DCFL
- DCFL ∩ Regular = DCFL
- DCFL - Regular = DCFL
- Regular - DCFL = Regular
- DCFL ∪ CFL = CFL (Need not be DCFL)
- DCFL ∩ CFL = Need not be CFL
- DCFL - CFL = Need not be CFL
- CFL - DCFL = Need not be CFL
- DCFL ∪ Finite = DCFL
- DCFL ∩ Finite = Finite
- DCFL - Finite = DCFL
- Finite - DCFL = Finite
Turing Machine
- Definition:
A Turing Machine (TM) is a mathematical model of computation used to define what can be computed.
Components:
- Q: Finite set of states.
- Σ: Input alphabet (does not include the blank symbol).
- Γ: Tape alphabet (Σ⊆Γ, includes the blank symbol).
- δ: Transition function.
- q₀: Initial state (q0∈Q\).
- q_accept: Accepting state.
- q_reject: Rejecting state (q_accept≠q_reject).
Transition Function:
- DTM: δ:Q×Γ→Q×Γ×{L,R}
- NTM: δ:Q×Γ→2Q×Γ×{L,R}
Types of Turing Machines:
- DTM (Deterministic TM): One transition for each state-symbol pair.
- NTM (Non-Deterministic TM): Multiple transitions for each state-symbol pair.
Language Classification:
- Turing Recognizable (Recursively Enumerable):
Languages accepted by a TM (TM halts for strings in the language but may loop for others). - Turing Decidable (Recursive):
Languages for which the TM halts on every input.
Special Types of TMs:
- Multi-Tape TM: Multiple tapes and heads; equivalent in power to a single-tape TM.
- Multi-Track TM: Single tape divided into multiple tracks.
- Non-Deterministic TM: Simulates multiple computation paths; equivalent in power to DTM.
- Universal TM: Simulates any TM by encoding its description.
Key Properties:
- TM can simulate Finite Automata and Pushdown Automata.
- TM is more powerful than DFA, NFA, and PDA.
- TM accepts Recursively Enumerable Languages.
Read more about Turing Machine in TOC, Here.
Church-Turing Thesis:
- Any computation performed by a mechanical process can be simulated by a Turing Machine.
Read about Chruch-Turing Thesis, Here.
Important Points:
- TMs are used to define Decidability and Undecidability.
- Halting Problem: Classic example of an undecidable problem.
- Equivalence of DTM and NTM: Both recognize the same set of languages.
- Multi-tape TMs are computationally equivalent to single-tape TMs but more efficient.
- Language accepted by NTM, multi-tape TM and DTM are same.
- Power of NTM, Multi-Tape TM and DTM is same.
- Every NTM can be converted to corresponding DTM.
Time Complexity:
- Deterministic TM: O(f(n)) for time complexity f(n).
- Non-Deterministic TM: O(2O(f(n))) in the worst case when converted to DTM.
Recursive and Recursive Enumerable Language
Recursive Language (Decidable Language): A language is recursive if there exists a Turing Machine (TM) that halts on every input and correctly decides whether the input is in the language.
Recognizable or Recursively Enumerable Language (Semi-Decidable Language): A language is recursively enumerable if there exists a Turing Machine (TM) that halts and accepts inputs that belong to the language, but it may loop forever for inputs not in the language.
Read about Recursive and Recursive Enumerable Language in TOC, Here.
Complement Property of Rec and RE Language:
Complement of Recursive set is Recursive.
Complement of RE is either Recursive or non-RE.
Complement of RE never be “RE which is not recursive”.
Closure Properties of RE and Rec Language
| Operation | Recursive Languages (Rec) | Recursively Enumerable Languages (RE) |
|---|
| Union | Closed | Closed |
| Intersection | Closed | Not Closed |
| Complement | Closed | Not Closed |
| Concatenation | Closed | Closed |
| Kleene Star | Closed | Closed |
| Difference | Closed | Not Closed |
| Reversal | Closed | Closed |
| Intersection with Regular | Closed | Closed |
Decidable Problems (Recursive Languages):
- A problem is decidable if there exists a Turing Machine (TM) that halts for all inputs (accepts for "yes" and rejects for "no").
- Examples include membership and equivalence problems for regular and context-free languages.
Undecidable Problems:
- Problems for which no Turing Machine (HTM) exists to solve them for all inputs.
- Further classified into:
- Recursively Enumerable (RE) but not Recursive:
- The problem is semi-decidable (a TM exists that halts for "yes" cases but may loop forever for "no").
- Not Recursively Enumerable (Not RE):
- No Turing Machine exists to even semi-decide the problem.
Read about Decidable and Undecidable Problem in TOC, Here.

Countability in Turing Machines
- Countable Set of Turing Machines:
- The set of all possible Turing Machines is countable because each Turing Machine can be encoded as a finite string (its description can be encoded using a finite alphabet, making it possible to enumerate all possible TMs).
- Uncountable Set of Languages:
- The set of all possible languages (subsets of all possible strings) is uncountable, as there are more possible languages than there are Turing Machines. This is due to the fact that we can define languages using infinite sets, and there are more subsets of an infinite set than the number of elements in the set.
Read more about Determining Countability in TOC, Here.
See Last Minute Notes on all subjects , here.
Similar Reads
Introduction to Theory of Computation Automata theory, also known as the Theory of Computation, is a field within computer science and mathematics that focuses on studying abstract machines to understand the capabilities and limitations of computation by analyzing mathematical models of how machines can perform calculations.Why we study
7 min read
TOC Basics
Regular Expressions & Finite Automata
Introduction of Finite AutomataFinite automata are abstract machines used to recognize patterns in input sequences, forming the basis for understanding regular languages in computer science. They consist of states, transitions, and input symbols, processing each symbol step-by-step. If the machine ends in an accepting state after
4 min read
Regular Expressions, Regular Grammar and Regular LanguagesTo work with formal languages and string patterns, it is essential to understand regular expressions, regular grammar, and regular languages. These concepts form the foundation of automata theory, compiler design, and text processing.Regular ExpressionsRegular expressions are symbolic notations used
7 min read
Arden's Theorem in Theory of ComputationA Regular Expression (RE) is a way to describe patterns of strings using symbols and operators like union, concatenation, and star. A Deterministic Finite Automaton (DFA) is a machine that reads input strings and decides if they match the pattern by moving through a set of defined states without any
6 min read
Conversion from NFA to DFAAn NFA can have zero, one or more than one move from a given state on a given input symbol. An NFA can also have NULL moves (moves without input symbol). On the other hand, DFA has one and only one move from a given state on a given input symbol. Steps for converting NFA to DFA:Step 1: Convert the g
5 min read
Minimization of DFADFA minimization stands for converting a given DFA to its equivalent DFA with minimum number of states. DFA minimization is also called as Optimization of DFA and uses partitioning algorithm.Minimization of DFA Suppose there is a DFA D < Q, Δ, q0, Δ, F > which recognizes a language L. Then the
7 min read
Reversing Deterministic Finite AutomataPrerequisite – Designing finite automata Reversal: We define the reversed language L^R \text{ of } L  to be the language L^R = \{ w^R \mid w \in L \} , where w^R := a_n a_{n-1} \dots a_1 a_0 \text{ for } w = a_0 a_1 \dots a_{n-1} a_n Steps to Reversal: Draw the states as it is.Add a new single accep
4 min read
Mealy and Moore Machines in TOCMoore and Mealy Machines are Transducers that help in producing outputs based on the input of the current state or previous state. In this article we are going to discuss Moore Machines and Mealy Machines, the difference between these two machinesas well as Conversion from Moore to Mealy and Convers
3 min read
CFG & PDA
Simplifying Context Free GrammarsA Context-Free Grammar (CFG) is a formal grammar that consists of a set of production rules used to generate strings in a language. However, many grammars contain redundant rules, unreachable symbols, or unnecessary complexities. Simplifying a CFG helps in reducing its size while preserving the gene
6 min read
Converting Context Free Grammar to Chomsky Normal FormChomsky Normal Form (CNF) is a way to simplify context-free grammars (CFGs) so that all production rules follow specific patterns. In CNF, each rule either produces two non-terminal symbols, or a single terminal symbol, or, in some cases, the empty string. Converting a CFG to CNF is an important ste
5 min read
Closure Properties of Context Free LanguagesContext-Free Languages (CFLs) are an essential class of languages in the field of automata theory and formal languages. They are generated by context-free grammars (CFGs) and are recognized by pushdown automata (PDAs). Understanding the closure properties of CFLs helps in determining which operation
11 min read
Pumping Lemma in Theory of ComputationThere are two Pumping Lemmas, which are defined for 1. Regular Languages, and 2. Context - Free Languages Pumping Lemma for Regular Languages For any regular language L, there exists an integer n, such that for all x ? L with |x| ? n, there exists u, v, w ? ?*, such that x = uvw, and (1) |uv| ? n (2
4 min read
Ambiguity in Context free Grammar and LanguagesContext-Free Grammars (CFGs) are essential in formal language theory and play a crucial role in programming language design, compiler construction, and automata theory. One key challenge in CFGs is ambiguity, which can lead to multiple derivations for the same string.Understanding Derivation in Cont
3 min read
Context-sensitive Grammar (CSG) and Language (CSL)Context-Sensitive Grammar - A Context-sensitive grammar is an Unrestricted grammar in which all the productions are of form - Where α and β are strings of non-terminals and terminals. Context-sensitive grammars are more powerful than context-free grammars because there are some languages that can be
2 min read
Introduction of Pushdown AutomataWe have already discussed finite automata. But finite automata can be used to accept only regular languages. Pushdown Automata is a finite automata with extra memory called stack which helps Pushdown automata to recognize Context Free Languages. This article describes pushdown automata in detail.Pus
5 min read
Turing Machine & Decidability
Problems on Finite Automata
DFA for Strings not ending with "THE"Problem - Accept Strings that not ending with substring "THE". Check if a given string is ending with "the" or not. The different forms of "the" which are avoided in the end of the string are: "THE", "ThE", "THe", "tHE", "thE", "The", "tHe" and "the" All those strings that are ending with any of the
12 min read
DFA of a string with at least two 0’s and at least two 1’sProblem - Draw deterministic finite automata (DFA) of a string with at least two 0’s and at least two 1’s. The first thing that come to mind after reading this question us that we count the number of 1's and 0's. Thereafter if they both are at least 2 the string is accepted else not accepted. But we
3 min read
DFA for accepting the language L = { anbm | n+m =even }ProblemDesign a deterministic finite automata(DFA) for accepting the language L = {an bm | n+m = even}Examples:Input: a a b b , n = 2, m = 2 2 + 2 = 4 (even)Output: ACCEPTEDInput: a a a b b b b ,n = 3, m = 43 + 4 = 7 (odd) Output: NOT ACCEPTEDInput: a a a b b b , n = 3, m = 33 + 3 = 6 (even)Output:
14 min read
DFA machines accepting odd number of 0’s or/and even number of 1’sPrerequisite - Designing finite automata Problem - Construct a DFA machine over input alphabet \sum_= {0, 1}, that accepts: Odd number of 0’s or even number of 1’s Odd number of 0’s and even number of 1’s Either odd number of 0’s or even number of 1’s but not the both together Solution - Let first d
3 min read
DFA of a string in which 2nd symbol from RHS is 'a'Draw deterministic finite automata (DFA) of the language containing the set of all strings over {a, b} in which 2nd symbol from RHS is 'a'. The strings in which 2nd last symbol is "a" are: aa, ab, aab, aaa, aabbaa, bbbab etc Input/Output INPUT : baba OUTPUT: NOT ACCEPTED INPUT: aaab OUTPUT: ACCEPTED
10 min read
Problems on PDA
Construct Pushdown Automata for all length palindromeA Pushdown Automata (PDA) is like an epsilon Non deterministic Finite Automata (NFA) with infinite stack. PDA is a way to implement context free languages. Hence, it is important to learn, how to draw PDA. Here, take the example of odd length palindrome:Que-1: Construct a PDA for language L = {wcw'
6 min read
Construct Pushdown automata for L = {0n1m2m3n | m,n ≥ 0}Prerequisite - Pushdown automata, Pushdown automata acceptance by final state Pushdown automata (PDA) plays a significant role in compiler design. Therefore there is a need to have a good hands on PDA. Our aim is to construct a PDA for L = {0n1m2m3n | m,n ≥ 0} Examples - Input : 00011112222333 Outpu
3 min read
Construct Pushdown automata for L = {a2mc4ndnbm | m,n ≥ 0}Pushdown Automata plays a very important role in task of compiler designing. That is why there is a need to have a good practice on PDA. Our objective is to construct a PDA for L = {a2mc4ndn bm | m,n ≥ 0} Example:Input: aaccccdbOutput: AcceptedInput: aaaaccccccccddbbOutput: AcceptedInput: acccddbOut
3 min read
NPDA for accepting the language L = {anbn | n>=1}Prerequisite: Basic knowledge of pushdown automata.Problem :Design a non deterministic PDA for accepting the language L = {an bn | n>=1}, i.e.,L = {ab, aabb, aaabbb, aaaabbbb, ......} In each of the string, the number of a's are followed by equal number of b's. ExplanationHere, we need to maintai
2 min read
NPDA for accepting the language L = {ambncm+n | m,n ≥ 1}The problem below require basic knowledge of Pushdown Automata.Problem Design a non deterministic PDA for accepting the language L = {am bn cm+n | m,n ≥ 1} for eg. ,L = {abcc, aabccc, abbbcccc, aaabbccccc, ......} In each of the string, the total sum of the number of 'a’ and 'b' is equal to the numb
2 min read
NPDA for accepting the language L = {aibjckdl | i==k or j==l,i>=1,j>=1}Prerequisite - Pushdown automata, Pushdown automata acceptance by final state Problem - Design a non deterministic PDA for accepting the language L = {a^i b^j c^k d^l : i==k or j==l, i>=1, j>=1}, i.e., L = {abcd, aabccd, aaabcccd, abbcdd, aabbccdd, aabbbccddd, ......} In each string, the numbe
3 min read
NPDA for accepting the language L = {anb2n| n>=1} U {anbn| n>=1}To understand this question, you should first be familiar with pushdown automata and their final state acceptance mechanism.ProblemDesign a non deterministic PDA for accepting the language L = {an b2n : n>=1} U {an bn : n>=1}, i.e.,L = {abb, aabbbb, aaabbbbbb, aaaabbbbbbbb, ......} U {ab, aabb
2 min read
Problems on Turing Machines
Turing Machine for additionPrerequisite - Turing Machine A number is represented in binary format in different finite automata. For example, 5 is represented as 101. However, in the case of addition using a Turing machine, unary format is followed. In unary format, a number is represented by either all ones or all zeroes. For
3 min read
Turing machine for multiplicationPrerequisite - Turing Machine Problem: Draw a turing machine which multiply two numbers. Example: Steps: Step-1. First ignore 0's, C and go to right & then if B found convert it into C and go to left. Step-2. Then ignore 0's and go left & then convert C into C and go right. Step-3. Then conv
2 min read
Construct a Turing Machine for language L = {wwr | w ∈ {0, 1}}The language L = {wwres | w ∈ {0, 1}} represents a kind of language where you use only 2 character, i.e., 0 and 1. The first part of language can be any string of 0 and 1. The second part is the reverse of the first part. Combining both these parts a string will be formed. Any such string that falls
5 min read
Construct a Turing Machine for language L = {ww | w ∈ {0,1}}Prerequisite - Turing Machine The language L = {ww | w ∈ {0, 1}} tells that every string of 0's and 1's which is followed by itself falls under this language. The logic for solving this problem can be divided into 2 parts: Finding the mid point of the string After we have found the mid point we matc
7 min read
Construct Turing machine for L = {an bm a(n+m) | n,m≥1}Problem : L = { anbma(n +m) | n , m ≥ 1} represents a kind of language where we use only 2 character, i.e., a and b. The first part of language can be any number of "a" (at least 1). The second part be any number of "b" (at least 1). The third part of language is a number of "a" whose count is sum o
3 min read
Construct a Turing machine for L = {aibjck | i*j = k; i, j, k ≥ 1}Prerequisite – Turing Machine In a given language, L = {aibjck | i*j = k; i, j, k ≥ 1}, where every string of 'a', 'b' and 'c' has a certain number of a's, then a certain number of b's and then a certain number of c's. The condition is that each of these 3 symbols should occur at least once. 'a' and
2 min read
Turing machine for 1's and 2’s complementProblem-1:Draw a Turing machine to find 1's complement of a binary number. 1’s complement of a binary number is another binary number obtained by toggling all bits in it, i.e., transforming the 0 bit to 1 and the 1 bit to 0. Example:1's ComplementApproach:Scanning input string from left to rightConv
3 min read
Practice