Design and Analysis of Algorithms
Download as pptx, pdf21 likes24,040 views
This document summarizes a lecture on algorithms and graph traversal techniques. It discusses: 1) Breadth-first search (BFS) and depth-first search (DFS) algorithms for traversing graphs. BFS uses a queue while DFS uses a stack. 2) Applications of BFS and DFS, including finding connected components, minimum spanning trees, and bi-connected components. 3) Identifying articulation points to determine biconnected components in a graph. 4) The 0/1 knapsack problem and approaches for solving it using greedy algorithms, backtracking, and branch and bound search.
![PRESENTED BY ARVIND KRISHNAA JALGORITHM FOR BFSvoid BFS(int v){//v being a starting vertexint u=v;Queue q[SIZE];visited[v]=1;do{for all vertices w adjacent to to u{ if(visited[w]==0)//w is unvisited {q.AddQ(w);visited[w]=1; }}if(Q.Empty()) return;q.Delete(u);}while(1);}](https://image.slidesharecdn.com/daapresentation-110531074801-phpapp01/85/Design-and-Analysis-of-Algorithms-12-320.jpg)
![PRESENTED BY ARVIND KRISHNAA JPERFORMING THE BREADTH FIRST TRAVERSALvoid BFT(graph G,int n){int i;boolean visited[SIZE];for(i=1;i<=n;i++)visited[i]=0;for(i=1;i<=n;i++)if(!visited[i]) BFS[i};}](https://image.slidesharecdn.com/daapresentation-110531074801-phpapp01/85/Design-and-Analysis-of-Algorithms-14-320.jpg)
![PRESENTED BY ARVIND KRISHNAA JALGORITHM FOR DFSvoid DFS(int v){visited[v]=1;for each vertex w adjacent to v { if(!visited[w]) DFS[w];}}](https://image.slidesharecdn.com/daapresentation-110531074801-phpapp01/85/Design-and-Analysis-of-Algorithms-16-320.jpg)
![SIMPLE ALGORITHM:Construct a DFS spanning tree for the given graphHave parameters dfn[u],L[u]Do a preorder traversal of the spanning tree and compute dfn[u] for each node as the ith node that is visitedCompute the value of L[u] asPRESENTED BY ARVIND KRISHNAA JIDENTIFYING ARTICULATION POINTSL[u]=min{ dfn[u],min{L[w]|w is a child of u}, min{ dfn[w] | (u,w) is a back edge}](https://image.slidesharecdn.com/daapresentation-110531074801-phpapp01/85/Design-and-Analysis-of-Algorithms-31-320.jpg)
![SIMPLE ALGORITHM:Nodes which satisfy L[w]≥dfn[u], w being the children of u are identified as articulation pointsSPECIAL CASE OF ROOT NODENote: The root node is always listed as an articulation pointif root node has exactly one childthen exclude the root node from AP listelseroot node is also an articulation pointPRESENTED BY ARVIND KRISHNAA JIDENTIFYING ARTICULATION POINTS contd...](https://image.slidesharecdn.com/daapresentation-110531074801-phpapp01/85/Design-and-Analysis-of-Algorithms-32-320.jpg)
![PRESENTED BY ARVIND KRISHNAA JTHE STATE-SPACE TREE(WITH BOUND)[PERFORMING A BFS TRAVERSAL]HENCE THE FINAL ANWER SET WOULD BEX={1,0,1,0}i.e., objects 1 and 3 are chosen...2 and 4 are discarded](https://image.slidesharecdn.com/daapresentation-110531074801-phpapp01/85/Design-and-Analysis-of-Algorithms-56-320.jpg)
More Related Content
What's hot (20)
Viewers also liked (17)
Similar to Design and Analysis of Algorithms (20)
More from Arvind Krishnaa (18)
Recently uploaded (20)
Design and Analysis of Algorithms
- 1. DESIGN AND ANALYSIS OF ALGORITHMSRemember this: “No problem is too tough if u spend enuf time on it” -A great manQuestion:an+bn=cn find a,b,c Answer: Ethoingayirukku!!an+bn=cn PRESENTED BY ARVIND KRISHNAA J
- 2. CONTENTS OF THE UNITGRAPH TRAVERSALS
- 6. BRANCH AND BOUND:GENERAL METHODS(FIFO & LC)
- 8. INTRODUCTION TO NP-HARD AND NPCOMPLETENESSPRESENTED BY ARVIND KRISHNAA JUNIT –V SYLLABUS
- 9. AIM:The main aim of any graph traversal algorithm is for a given graph G=(V,E) is to determine whether there exists a path starting from a vertex v to a vertex uPRESENTED BY ARVIND KRISHNAA JGRAPH TRAVERSALS
- 10. PRESENTED BY ARVIND KRISHNAA JGRAPH TRAVERSALS
- 11. PRESENTED BY ARVIND KRISHNAA JBREADTH FIRST SEARCHBASIC IDEA:Visits graph vertices by moving across to all the neighbors of last visited vertex b BFS uses a queuea vertex is inserted into queue when it is reached for the first time, and is marked as visited.a vertex is removed from the queue, when it identifies all unvisited vertices that are adjacent to the vertex b
- 12. PRESENTED BY ARVIND KRISHNAA JALGORITHM FOR BFSvoid BFS(int v){//v being a starting vertexint u=v;Queue q[SIZE];visited[v]=1;do{for all vertices w adjacent to to u{ if(visited[w]==0)//w is unvisited {q.AddQ(w);visited[w]=1; }}if(Q.Empty()) return;q.Delete(u);}while(1);}
- 13. PRESENTED BY ARVIND KRISHNAA JAN EXAMPLE GRAPH12364578
- 14. PRESENTED BY ARVIND KRISHNAA JPERFORMING THE BREADTH FIRST TRAVERSALvoid BFT(graph G,int n){int i;boolean visited[SIZE];for(i=1;i<=n;i++)visited[i]=0;for(i=1;i<=n;i++)if(!visited[i]) BFS[i};}
- 15. PRESENTED BY ARVIND KRISHNAA JDEPTH FIRST SEARCHBASIC IDEAStarting vertex is arbitrarily chosen or determined by the problem.Visits graph’s vertices by always moving away from last visited vertex to unvisited one, backtracks if no adjacent unvisited vertex is available.Uses a stacka vertex is pushed onto the stack when it’s reached for the first timea vertex is popped off the stack when it becomes a dead end, i.e., when there is no adjacent unvisited vertex
- 16. PRESENTED BY ARVIND KRISHNAA JALGORITHM FOR DFSvoid DFS(int v){visited[v]=1;for each vertex w adjacent to v { if(!visited[w]) DFS[w];}}
- 17. PRESENTED BY ARVIND KRISHNAA Jfor the graph.....ABDEC
- 18. PRESENTED BY ARVIND KRISHNAA JAPPLICATIONSBREADTH FIRST SEARCH:Greedy graph algorithmsfinding the minimum spanning tree using PRIM’S ALGORITHMsingle source (or) all pair shortest path using DIJKSTRA’S ALGORITHMNETWORK FLOW PROBLEMTesting for connected componentsDEPTH FIRST SEARCH:Testing for biconnected components(bi-connectivity)for eg., checking for the connectivity of a network
- 19. PRESENTED BY ARVIND KRISHNAA JCONNECTED COMPONENTSDEFINITION:Two vertices in a graph are in the same connected component if and only if there is a path from one vertex to the otherNOTE:BFS algorithm can be used to test whether a graph is connected or notIf a graph G is connected then only 1 call to the function BFT(G,n) is made
- 20. The number of calls made to the BFT function can be used to roughly determine the number of “disconnected” componentsPRESENTED BY ARVIND KRISHNAA JDETERMINING A CONNECTED COMPONENTSTRATEGYAll newly visited vertices on a call to BFS represent vertices in a connected component of GTo display the connected components modify BFS to put newly visited vertices into a listConsider for the graph discussed previously.....
- 21. PRESENTED BY ARVIND KRISHNAA JFOR THE DIRECTED GRAPHABCEDF
- 22. PRESENTED BY ARVIND KRISHNAA JTHE DFS LIST ISELIST MADE IN THE FIRST CALLLIST MADE DURING THE SECOND CALLAs the number of calls made to the function is 2 it means that the graph is not connectedThere are two sets of connected components represented above
- 23. PRESENTED BY ARVIND KRISHNAA JSPANNING TREEBFS SPANNING TREE1BFS SPANNING TREE:A spanning tree constructed by performing the Breadth first search of a graph2364578
- 24. PRESENTED BY ARVIND KRISHNAA JSPANNING TREEDFS SPANNING TREE1DFS SPANNING TREE:A spanning tree constructed by performing the Depth first search of a graph2364578
- 25. PRESENTED BY ARVIND KRISHNAA JBICONNECTED COMPONENTSNOTE: Henceforth the word “Graph” would be used instead of the term “undirected Graph”ARTICULATION POINT: A vertex v in a connected graph is said to be an articulation point if and only if the the deletion of the vertex v and all its edges incident to it “disconnects” the graph into two or more non-empty components.Biconnected graph: A graph G is said to be biconnected if and only if it contains no articulation pointsLet us see an example....
- 26. PRESENTED BY ARVIND KRISHNAA JA connected graph156247The articulation points are highlighted...removing them causes disconnection83109
- 27. PRESENTED BY ARVIND KRISHNAA JPOINTS TO NOTE LEMMA: Two biconnected components can have at most one vertex in common and this vertex is an articulation point.TRANSLATION: The common vertex of two biconnected components is an articulation point.NOTE: No edge can be in two different biconnected components as this would require two common vertices(violation of Lemma!!)
- 28. PRESENTED BY ARVIND KRISHNAA JMAKING A CONNECTED GRAPH BICONNECTEDTECHNIQUE:Simply add “redundant” edges between the connected components that have the articulation point (say a) in common...for example the previously discussed connected graph can be made biconnected by adding the throbbing links(see next slide...if u r asleep pls continue...)
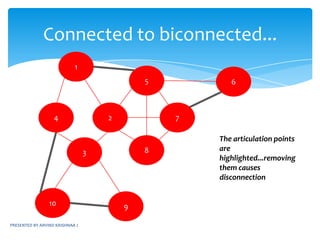
- 29. PRESENTED BY ARVIND KRISHNAA JConnected to biconnected...156247The articulation points are highlighted...removing them causes disconnection83109
- 30. PRESENTED BY ARVIND KRISHNAA JSCHEME TO CONSTRUCT A BICONNECTED COMPONENTfor each articulation point a{let B1,B2,…Bk be the biconnected components containing vertex a; let vi,vi≠a, be a vertex in Bi , 1≤i≤k;add to G the edges (vi,vi+1),1≤i≤k;}
- 31. SIMPLE ALGORITHM:Construct a DFS spanning tree for the given graphHave parameters dfn[u],L[u]Do a preorder traversal of the spanning tree and compute dfn[u] for each node as the ith node that is visitedCompute the value of L[u] asPRESENTED BY ARVIND KRISHNAA JIDENTIFYING ARTICULATION POINTSL[u]=min{ dfn[u],min{L[w]|w is a child of u}, min{ dfn[w] | (u,w) is a back edge}
- 32. SIMPLE ALGORITHM:Nodes which satisfy L[w]≥dfn[u], w being the children of u are identified as articulation pointsSPECIAL CASE OF ROOT NODENote: The root node is always listed as an articulation pointif root node has exactly one childthen exclude the root node from AP listelseroot node is also an articulation pointPRESENTED BY ARVIND KRISHNAA JIDENTIFYING ARTICULATION POINTS contd...
- 33. PRESENTED BY ARVIND KRISHNAA JCOMPUTATIONS FOR THE GIVEN GRAPH
- 34. Oh MahaZeeya..Oh MahaZeeya..NakkaMukkaNakka...Oh Shakalakka..Oh Randakka..(x2)Oh Laahi Oh Laahi..AyakaYahiYahi..Me Hoo..Me Hoo...DailamoDailamo..RahtullaSonali Oh..Oh MahaZeeya..Oh MahaZeeya..NakkaMukkaNakka...Oh Shakalakka..Oh Randakka..Samba Sambale..OsoseSayoSayo..HasiliFisili..Ilahi..YappaJippa..(x2)blah blahblablabla.......PRESENTED BY ARVIND KRISHNAA JRECAP OF YESTERDAY
- 35. Branch & Bound
- 36. Review of Backtracking 1. Construct the state-space tree• nodes: partial solutions• edges: choices in extending partial solutions2. Explore the state space tree using depth-first search3. “Prune” nonpromising nodes• dfs stops exploring subtrees rooted at nodes that cannotlead to a solution and backtracks to such a node’sparent to continue the search
- 37. Branch-and-BoundAn enhancement of backtracking
- 38. Applicable to optimization problems
- 39. Breadth first search(FIFO B&B) or D-search(LIFO B&B) is performed on the state space tree
- 40. For each node (partial solution) of a state-space tree, computes a bound on the value of the objective function for all descendants of the node (extensions of the partial solution)
- 41. Uses the bound for:
- 42. ruling out certain nodes as “nonpromising” to prune the tree – if a node’s bound is not better than the best solution seen so far
- 43. guiding the search through state-spaceExample: Assignment ProblemSelect one element in each row of the cost matrix C so that: no two selected elements are in the same column
- 44. the sum is minimizedExampleJob1Job2Job3Job4 Person a 9 2 7 8 Person b 6 4 3 7 Person c 5 8 1 8 Person d 7 6 9 4Lower bound: Any solution to this problem will have total cost at least: 2 + 3 + 1 + 4 (or 5 + 2 + 1 + 4)N people n jobs cost should be small.
- 45. Example: First two levels of the state-space tree
- 46. ExplanationSelect 1st element from first row i.e9Select minimum from remaining rows 3, 1, 4 not from 1st columnSo 9+3+1+4 = 17.Select 2nd element from first row i.e2Select minimum from remaining rows 3, 1, 4 not from 2nd columnSo 2+3+1+4 = 10.Select 3rd element from first row i.e7Select minimum from remaining rows 3, 1, 4 not from 3rdcolumnSo 7+4+5+4 = 20.Last one it is 8+3+1+6 = 18
- 47. Example (cont.)
- 48. Explanation(contd...)1. Select 2nd element from first row i.e 2Select 1st element from second row i.e 6Select minimum from remaining rows 1, 4 not from 1st columnSo 2+6+1+4 = 13.2. Select 2nd element from first row i.e 2Cannot Select 2nd element from second row 3. Select 2nd element from first row i.e 2Select 3rd element from third row i.e 3Select minimum from remaining rows 5, 4 not from 3rd columnSo 2+3+5+4 = 14.4. 2 + 7 + 1+7 =17Note: Promising node is live node a->2 is live node.
- 49. Example: Complete state-space tree
- 51. Branch and boundApplicable to optimization problemThe state space tree is generated using best first rule.PRESENTED BY ARVIND KRISHNAA JCOMPARISON OF B&B AND BACKTRACKINGBacktrackingNot constrained but mostly applied to Non-optimization problem
- 52. The state space tree is generated using DFSGreedy Algorithm for Knapsack ProblemStep 1: Order the items in decreasing order of relative values: v1/w1… vn/wnStep 2: Select the items in this order skipping those that don’t fit into the knapsackExample: The knapsack’s capacity is 15i Pi WiPi/Wi 1 $45 3 $15 2 $30 5 $ 6 3 $45 9 $ 5 4 $10 5 $ 2
- 53. Branch and Bound Scheme for Knapsack ProblemStep 1: Order the items in decreasing order of relative values: v1/w1… vn/wnStep 2: For a given integer parameter k, 0 ≤ k ≤ n, generate allsubsets of k items or less and for each of those that fit the knapsack, add the remaining items in decreasingorder of their value to weight ratiosStep 3: Find the most valuable subset among the subsets generated in Step 2 and return it as the algorithm’s output
- 54. bound (maximum potential value) = currentValue + value of remaining objects fully placed + (K - totalSize) * (value density of item that is partially placed) PRESENTED BY ARVIND KRISHNAA JSOME THINGS TO NOTEtotalSize = currentSize + size of remaining objects that can be fully placed
- 55. k-1bound = currentValue+∑ vj + (K - totalSize) * (vk/sk)j=i+1For the root node, currentSize = 0, currentValue = 0PRESENTED BY ARVIND KRISHNAA JIN FORMULAEk-1totalSize = currentSize + ∑ sjj=i+1
- 56. PRESENTED BY ARVIND KRISHNAA JTHE STATE-SPACE TREE(WITH BOUND)[PERFORMING A BFS TRAVERSAL]HENCE THE FINAL ANWER SET WOULD BEX={1,0,1,0}i.e., objects 1 and 3 are chosen...2 and 4 are discarded
- 57. WHAT THE PREVIOUS PROBLEM DIDStep 1: We will construct the state space where each node contains the total current value in the knapsack, the total current size of the contents of the knapsack, and maximum potential value that the knapsack can hold. In the algorithm, we will also keep a record of the maximum value of any node (partially or completely filled knapsack) found so far.Step 2: Perform the breadth first traversal of the state space tree computing the bound and totalsizeStep 3: Discard(prune)those “non-promising nodes” which either have(a) a lower bound than the other nodes at same level (b) whose size exceeds the total knapsack capacityStep 4: The above method involving the BFS of the state space tree is called FIFO BRANCH & BOUND ALGORITHM
- 58. LC ALGORITHM(LEAST COST)This is a generic form/generalization of both the BFS and DFS algorithms
- 59. In LC algorithm a traversal is performed on the state space tree
- 60. Each node is given a rank based on a minimization rule(also known as best first rule) f(x)(in case of the Knapsack problem the minimization rule can be stated as f(x)=--g(x),where g(x) is the maximization rule for the Knapsack problem)Once all nodes have been ranked eliminate/prune the nodes with the poorest ranks.
- 61. Repeat till a feasible solution is obtained(sorry i cant go into too much further detail....its getting too mathematical...)
- 63. Polynomial Time: Algorithms whose solution is found in polynomial timeeg., Sorting, searching etc.,Non-polynomial Time: Algorithms which DO NOT take polynomial time to find the solutioneg., Travelling salesperson problem (O(n22n)) PRESENTED BY ARVIND KRISHNAA JTWO KINDS OF ALGORITHMS
- 64. Problems for which there is no polynomial time complexity, are computationally relatedThere are two classes of such problems1. NP HARD AND 2. NP COMPLETEPRESENTED BY ARVIND KRISHNAA JTWO KINDS OF ALGORITHMS
- 65. The problem that is NP complete has the property that it can be solved in polynomial time if and only if all the other NP complete problems can be solved in polynomial timePRESENTED BY ARVIND KRISHNAA JNP COMPLETE
- 66. If an NP-hard problem can be solved in ploynomial time, then all NP complete problems can also be solved in polynomial time.PRESENTED BY ARVIND KRISHNAA JNP HARD
- 67. PRESENTED BY ARVIND KRISHNAA JSET REPRESENTATION OF THE ABOVE STATEMENTSNPNP HARDPNP COMPLETE
- 68. Deterministic Algorithm: Has the property that result of every operation is uniquely definedNon-Deterministic Algorithm: Outcome of an operation is not uniquely definedPRESENTED BY ARVIND KRISHNAA JNON DETERMINISTIC ALGORITHMS
- 69. Every non-deterministic algorithm makes use of three functionschoice(S): arbitrarily choosing an element in a s et S for eg., x=choice(1,n) | means x€[1,n]failure(): unsuccessful completionsuccess(): successful completionPRESENTED BY ARVIND KRISHNAA JTHREE NEW FUNCTIONS
- 70. NON DETERMINISTIC SEARCHINGND SORTINGMAXIMUM CLIQUE PROBLEM0/1 KANPSACK PROBLEMSATISFIABLITYand many, many morePRESENTED BY ARVIND KRISHNAA JSOME EXAMPLES OF NON-DETERMINISTIC ALGORITHMS
- 71. nondeterministic_search(x){int j=choice(1,n);if(A[j]==x){cout<<j; success(); }cout<<‘0’;failure();}PRESENTED BY ARVIND KRISHNAA JNON DETERMINISTIC SEARCHING
- 72. voidnondeterministic_sort(int A[],int n){int B[SIZE],i,j;for(i=1;i<=n;i++) B[i]=0;for(i=1;i<=n;i++){ j=choice(1,n); if(B[j]) failure(); B[j]=A[i];}for(i=1;i<=n;i++)//verify order if(B[i] > B[i+1]) failure();for(i=1;i<=n;i++)cout<<B[i]<<‘ ‘;success();}PRESENTED BY ARVIND KRISHNAA JNON DETERMINISTIC SORTING
- 73. void DCK(int G[]{SIZE],intn,int k){S=null;//initially emptyfor(int i=1;i<=k;i++){int t=choice(1,n); if(t is in S) failure(); S=S U {t};}//now S contains k distinct verticesfor(all pairs (i,j) such that i is in S,j is in S and i!=j) if((i,j) is not an edge of G) failure();success();}PRESENTED BY ARVIND KRISHNAA JNON DETERMINISTIC Clique
- 74. void DKP(int p[],int w[],intn,intm,intr,int x[]){int W=0,P=0;for(int i=1;i<=n;i++){ x[i]=choice(0,1); W+=x[i]*w[i]; P+=x[i]*p[i];}if((W>m) || (P < r)) failure();else success();}PRESENTED BY ARVIND KRISHNAA JNON DETERMINISTIC KNAPSACK
- 75. void eval(cnfE,int n)//determine whether the prop. formula is satisfiable//variables are x[1],x[2],x[3],...x[n]{int x[SIZE];//choose a truth value assignmentfor(int i=1;i<=n;i++)x[i]=choice(0,1);if(E(x,n))success();else failure();}PRESENTED BY ARVIND KRISHNAA JNON DETERMINISTIC SATISFIABLITY
- 76. GRAPH PROBLEMS LIKENODE COVERING PROBLEMGRAPH COMPLEMENT PROBLEMSCHEDULING PROBLEMSCODE GENERATION PROBLEMand many morePRESENTED BY ARVIND KRISHNAA JSOME EXAMPLES OF NP HARD PROBLEMS
- 77. CHECK OUT THE TEXTBOOKPAGE NO571PRESENTED BY ARVIND KRISHNAA JSOME EXAMPLES OF NP complete PROBLEMS
- 78. APPROXIMATIONRANDOMIZATIONRESTRICTIONPARAMETRIZATIONHEURISTICSPRESENTED BY ARVIND KRISHNAA JBASIC TEHNIQUES INVOLVED IN SOLVING NP COMPLETE PROBLEMSOR IN SHORT PERFORMING A NON-DETERMINISTIC ANALYSIS ON THE PROBLEM
- 79. ONE FINAL QUESTIONRemember this: “No problem is too tough if u spend enuf time on it” -A great manPRESENTED BY ARVIND KRISHNAA JWHO IS THIS GREAT MAN???
- 80. THANK YOU!!!!!PRESENTED BY ARVIND KRISHNAA J