A geometrical approach in Linear Programming Problems
- 1. 6 Graphing Systems of Linear Inequalities in Two Variables Linear Programming Problems Graphical Solutions of Linear Programming Problems The Simplex Method: Standard Maximization Problems The Simplex Method: Standard Minimization Problems Linear Programming: A Geometric Approach
- 2. 6.1 Graphing Systems of Linear Inequalities in Two Variables xx yy 44xx + 3+ 3yy == 1212 12 12 7 7( , )P 12 12 7 7( , )P xx –– yy == 00 4 3 12 0 x y x y 4 3 12 0 x y x y 44 33 22 11 ––11 11 22 33
- 3. Graphing Linear Inequalities We’ve seen that a linear equation in two variables x and y has a solution set that may be exhibited graphically as points on a straight line in the xy-plane. There is also a simple graphical representation for linear inequalities of two variables: 0ax by c 0ax by c 0ax by c 0ax by c 0ax by c
- 4. Procedure for Graphing Linear Inequalities 1. Draw the graph of the equation obtained for the given inequality by replacing the inequality sign with an equal sign. ✦ Use a dashed or dotted line if the problem involves a strict inequality, < or >. ✦ Otherwise, use a solid line to indicate that the line itself constitutes part of the solution. 2. Pick a test point lying in one of the half-planes determined by the line sketched in step 1 and substitute the values of x and y into the given inequality. ✦ Use the origin whenever possible. 3. If the inequality is satisfied, the graph of the inequality includes the half-plane containing the test point. ✦ Otherwise, the solution includes the half-plane not containing the test point.
- 5. Examples Determine the solution set for the inequality 2x + 3y 6. Solution Replacing the inequality with an equality =, we obtain the equation 2x + 3y = 6, whose graph is: x y 7 5 3 1 –1 –5 –3 –1 1 3 5 2x + 3y = 6
- 6. Examples Determine the solution set for the inequality 2x + 3y 6. Solution Picking the origin as a test point, we find 2(0) + 3(0) 6, or 0 6, which is false. Thus, the solution set is: x y 7 5 3 1 –1 –5 –3 –1 1 3 5 2x + 3y = 6 2x + 3y 6 (0, 0)
- 7. Graphing Systems of Linear Inequalities The solution set of a system of linear inequalities in two variables x and y is the set of all points (x, y) that satisfy each inequality of the system. The graphical solution of such a system may be obtained by graphing the solution set for each inequality independently and then determining the region in common with each solution set.
- 8. –5 –3 1 3 5 Examples Graph x – 3y > 0. Solution Replacing the inequality > with an equality =, we obtain the equation x – 3y = 0, whose graph is: x y 3 1 –1 –3 x – 3y = 0
- 9. Examples Graph x – 3y > 0. Solution We use a dashed line to indicate the line itself will not be part of the solution, since we are dealing with a strict inequality >. x y x – 3y = 0 –5 –3 1 3 5 3 1 –1 –3
- 10. –5 –3 1 3 5 3 1 –1 –3 Examples Graph x – 3y > 0. Solution Since the origin lies on the line, we cannot use the origin as a testing point: x y x – 3y = 0 (0, 0)
- 11. Examples Graph x – 3y > 0. Solution Picking instead (3, 0) as a test point, we find (3) – 2(0) > 0, or 3 > 0, which is true. Thus, the solution set is: y x – 3y = 0 x – 3y > 0 –5 –3 1 3 5 3 1 –1 –3 x (3, 0)
- 12. Graphing Systems of Linear Inequalities The solution set of a system of linear inequalities in two variables x and y is the set of all points (x, y) that satisfy each inequality of the system. The graphical solution of such a system may be obtained by graphing the solution set for each inequality independently and then determining the region in common with each solution set.
- 13. Example Determine the solution set for the system Solution The intersection of the solution regions of the two inequalities represents the solution to the system: 4 3 12 0 x y x y x y 4 3 2 1 4x + 3y 12 4x + 3y = 12 –1 1 2 3
- 14. Example Determine the solution set for the system Solution The intersection of the solution regions of the two inequalities represents the solution to the system: 4 3 12 0 x y x y x y x – y 0 x – y = 0 4 3 2 1 –1 1 2 3
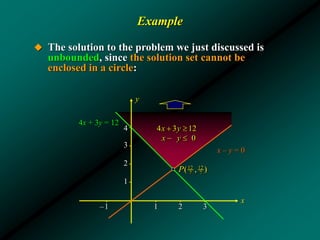
- 15. Example Determine the solution set for the system Solution The intersection of the solution regions of the two inequalities represents the solution to the system: 4 3 12 0 x y x y x y 4x + 3y = 12 x – y = 0 4 3 12 0 x y x y 4 3 2 1 –1 1 2 3 12 12 7 7( , )P
- 16. Bounded and Unbounded Sets The solution set of a system of linear inequalities is bounded if it can be enclosed by a circle. Otherwise, it is unbounded.
- 17. Example The solution to the problem we just discussed is unbounded, since the solution set cannot be enclosed in a circle: x y 4x + 3y = 12 12 12 7 7( , )P x – y = 0 4 3 12 0 x y x y 4 3 2 1 –1 1 2 3
- 18. 7 5 3 1 –1 1 3 5 9 Example Determine the solution set for the system Solution The intersection of the solution regions of the four inequalities represents the solution to the system: 6 0 2 8 0 0 0x y x y x y x y 2 8 0x y 6 0x y (2,4)P
- 19. Example Determine the solution set for the system Solution Note that the solution to this problem is bounded, since it can be enclosed by a circle: 6 0 2 8 0 0 0x y x y x y –1 1 3 5 9 x y 7 5 3 1 6 0x y (2,4)P 2 8 0x y
- 20. 6.2 Linear Programming Problems 0 0 x y 1.2P x y 3 300x y 2 180x y Maximize Subject to
- 21. Linear Programming Problem A linear programming problem consists of a linear objective function to be maximized or minimized subject to certain constraints in the form of linear equations or inequalities.
- 22. Applied Example 1: A Production Problem Ace Novelty wishes to produce two types of souvenirs: type-A will result in a profit of $1.00, and type-B in a profit of $1.20. To manufacture a type-A souvenir requires 2 minutes on machine I and 1 minute on machine II. A type-B souvenir requires 1 minute on machine I and 3 minutes on machine II. There are 3 hours available on machine I and 5 hours available on machine II. How many souvenirs of each type should Ace make in order to maximize its profit?
- 23. Applied Example 1: A Production Problem Solution Let’s first tabulate the given information: Let x be the number of type-A souvenirs and y the number of type-B souvenirs to be made. Type-A Type-B Time Available Profit/Unit $1.00 $1.20 Machine I 2 min 1 min 180 min Machine II 1 min 3 min 300 min
- 24. Applied Example 1: A Production Problem Solution Let’s first tabulate the given information: Then, the total profit (in dollars) is given by which is the objective function to be maximized. 1.2P x y Type-A Type-B Time Available Profit/Unit $1.00 $1.20 Machine I 2 min 1 min 180 min Machine II 1 min 3 min 300 min
- 25. Applied Example 1: A Production Problem Solution Let’s first tabulate the given information: The total amount of time that machine I is used is and must not exceed 180 minutes. Thus, we have the inequality 2x y 2 180x y Type-A Type-B Time Available Profit/Unit $1.00 $1.20 Machine I 2 min 1 min 180 min Machine II 1 min 3 min 300 min
- 26. Applied Example 1: A Production Problem Solution Let’s first tabulate the given information: The total amount of time that machine II is used is and must not exceed 300 minutes. Thus, we have the inequality 3x y 3 300x y Type-A Type-B Time Available Profit/Unit $1.00 $1.20 Machine I 2 min 1 min 180 min Machine II 1 min 3 min 300 min
- 27. Applied Example 1: A Production Problem Solution Let’s first tabulate the given information: Finally, neither x nor y can be negative, so 0 0 x y Type-A Type-B Time Available Profit/Unit $1.00 $1.20 Machine I 2 min 1 min 180 min Machine II 1 min 3 min 300 min
- 28. Applied Example 1: A Production Problem Solution In short, we want to maximize the objective function subject to the system of inequalities We will discuss the solution to this problem in section 6.4. 0 0 x y 1.2P x y 3 300x y 2 180x y
- 29. Applied Example 2: A Nutrition Problem A nutritionist advises an individual who is suffering from iron and vitamin B deficiency to take at least 2400 milligrams (mg) of iron, 2100 mg of vitamin B1, and 1500 mg of vitamin B2 over a period of time. Two vitamin pills are suitable, brand-A and brand-B. Each brand-A pill costs 6 cents and contains 40 mg of iron, 10 mg of vitamin B1, and 5 mg of vitamin B2. Each brand-B pill costs 8 cents and contains 10 mg of iron and 15 mg each of vitamins B1 and B2. What combination of pills should the individual purchase in order to meet the minimum iron and vitamin requirements at the lowest cost?
- 30. Applied Example 2: A Nutrition Problem Solution Let’s first tabulate the given information: Let x be the number of brand-A pills and y the number of brand-B pills to be purchased. Brand-A Brand-B Minimum Requirement Cost/Pill 6¢ 8¢ Iron 40 mg 10 mg 2400 mg Vitamin B1 10 mg 15 mg 2100 mg Vitamin B2 5mg 15 mg 1500 mg
- 31. Applied Example 2: A Nutrition Problem Solution Let’s first tabulate the given information: The cost C (in cents) is given by and is the objective function to be minimized. Brand-A Brand-B Minimum Requirement Cost/Pill 6¢ 8¢ Iron 40 mg 10 mg 2400 mg Vitamin B1 10 mg 15 mg 2100 mg Vitamin B2 5mg 15 mg 1500 mg 6 8C x y
- 32. Applied Example 2: A Nutrition Problem Solution Let’s first tabulate the given information: The amount of iron contained in x brand-A pills and y brand-B pills is given by 40x + 10y mg, and this must be greater than or equal to 2400 mg. This translates into the inequality Brand-A Brand-B Minimum Requirement Cost/Pill 6¢ 8¢ Iron 40 mg 10 mg 2400 mg Vitamin B1 10 mg 15 mg 2100 mg Vitamin B2 5mg 15 mg 1500 mg 40 10 2400x y
- 33. Applied Example 2: A Nutrition Problem Solution Let’s first tabulate the given information: The amount of vitamin B1 contained in x brand-A pills and y brand-B pills is given by 10x + 15y mg, and this must be greater or equal to 2100 mg. This translates into the inequality Brand-A Brand-B Minimum Requirement Cost/Pill 6¢ 8¢ Iron 40 mg 10 mg 2400 mg Vitamin B1 10 mg 15 mg 2100 mg Vitamin B2 5mg 15 mg 1500 mg 10 15 2100x y
- 34. Applied Example 2: A Nutrition Problem Solution Let’s first tabulate the given information: The amount of vitamin B2 contained in x brand-A pills and y brand-B pills is given by 5x + 15y mg, and this must be greater or equal to 1500 mg. This translates into the inequality Brand-A Brand-B Minimum Requirement Cost/Pill 6¢ 8¢ Iron 40 mg 10 mg 2400 mg Vitamin B1 10 mg 15 mg 2100 mg Vitamin B2 5mg 15 mg 1500 mg 5 15 1500x y
- 35. Applied Example 2: A Nutrition Problem Solution In short, we want to minimize the objective function subject to the system of inequalities We will discuss the solution to this problem in section 6.4. 5 15 1500x y 6 8C x y 40 10 2400x y 10 15 2100x y 0 0 x y
- 36. 6.3 Graphical Solutions of Linear Programming Problems 200200 100100 100100 200200 300300 xx yy SS10 15 2100x y 10 15 2100x y 40 10 2400x y 40 10 2400x y 5 15 1500x y 5 15 1500x y CC(120, 60)(120, 60) DD(300, 0)(300, 0) AA(0, 240)(0, 240) BB(30, 120)(30, 120)
- 37. Feasible Solution Set and Optimal Solution The constraints in a linear programming problem form a system of linear inequalities, which have a solution set S. Each point in S is a candidate for the solution of the linear programming problem and is referred to as a feasible solution. The set S itself is referred to as a feasible set. Among all the points in the set S, the point(s) that optimizes the objective function of the linear programming problem is called an optimal solution.
- 38. Theorem 1 Linear Programming If a linear programming problem has a solution, then it must occur at a vertex, or corner point, of the feasible set S associated with the problem. If the objective function P is optimized at two adjacent vertices of S, then it is optimized at every point on the line segment joining these vertices, in which case there are infinitely many solutions to the problem.
- 39. Theorem 2 Existence of a Solution Suppose we are given a linear programming problem with a feasible set S and an objective function P = ax + by. a. If S is bounded, then P has both a maximum and a minimum value on S. b. If S is unbounded and both a and b are nonnegative, then P has a minimum value on S provided that the constraints defining S include the inequalities x 0 and y 0. c. If S is the empty set, then the linear programming problem has no solution: that is, P has neither a maximum nor a minimum value.
- 40. The Method of Corners 1. Graph the feasible set. 2. Find the coordinates of all corner points (vertices) of the feasible set. 3. Evaluate the objective function at each corner point. 4. Find the vertex that renders the objective function a maximum or a minimum. ✦ If there is only one such vertex, it constitutes a unique solution to the problem. ✦ If there are two such adjacent vertices, there are infinitely many optimal solutions given by the points on the line segment determined by these vertices.
- 41. Applied Example 1: A Production Problem Recall Applied Example 1 from the last section (3.2), which required us to find the optimal quantities to produce of type-A and type-B souvenirs in order to maximize profits. We restated the problem as a linear programming problem in which we wanted to maximize the objective function subject to the system of inequalities We can now solve the problem graphically. 0 0 x y 1.2P x y 3 300x y 2 180x y
- 42. 200 100 100 200 300 Applied Example 1: A Production Problem We first graph the feasible set S for the problem. ✦ Graph the solution for the inequality considering only positive values for x and y: 2 180x y x y 2 180x y (90, 0) (0, 180) 2 180x y
- 43. 200 100 Applied Example 1: A Production Problem We first graph the feasible set S for the problem. ✦ Graph the solution for the inequality considering only positive values for x and y: 3 300x y 100 200 300 x y 3 300x y (0, 100) (300, 0) 3 300x y
- 44. 200 100 Applied Example 1: A Production Problem We first graph the feasible set S for the problem. ✦ Graph the intersection of the solutions to the inequalities, yielding the feasible set S. (Note that the feasible set S is bounded) 100 200 300 x y S 3 300x y 2 180x y
- 45. 200 100 Applied Example 1: A Production Problem Next, find the vertices of the feasible set S. ✦ The vertices are A(0, 0), B(90, 0), C(48, 84), and D(0, 100). 100 200 300 x y S C(48, 84) 3 300x y 2 180x y D(0, 100) B(90, 0)A(0, 0)
- 46. 200 100 Applied Example 1: A Production Problem Now, find the values of P at the vertices and tabulate them: 100 200 300 x y S C(48, 84) 3 300x y 2 180x y D(0, 100) B(90, 0)A(0, 0) Vertex P = x + 1.2 y A(0, 0) 0 B(90, 0) 90 C(48, 84) 148.8 D(0, 100) 120
- 47. 200 100 Applied Example 1: A Production Problem Finally, identify the vertex with the highest value for P: ✦ We can see that P is maximized at the vertex C(48, 84) and has a value of 148.8. 100 200 300 x y S 3 300x y 2 180x y D(0, 100) B(90, 0)A(0, 0) Vertex P = x + 1.2 y A(0, 0) 0 B(90, 0) 90 C(48, 84) 148.8 D(0, 100) 120 C(48, 84)
- 48. Applied Example 1: A Production Problem Finally, identify the vertex with the highest value for P: ✦ We can see that P is maximized at the vertex C(48, 84) and has a value of 148.8. ✦ Recalling what the symbols x, y, and P represent, we conclude that ACE Novelty would maximize its profit at $148.80 by producing 48 type-A souvenirs and 84 type-B souvenirs.
- 49. Applied Example 2: A Nutrition Problem Recall Applied Example 2 from the last section (3.2), which asked us to determine the optimal combination of pills to be purchased in order to meet the minimum iron and vitamin requirements at the lowest cost. We restated the problem as a linear programming problem in which we wanted to minimize the objective function subject to the system of inequalities We can now solve the problem graphically. 5 15 1500x y 6 8C x y 40 10 2400x y 10 15 2100x y , 0x y
- 50. 200 100 Applied Example 2: A Nutrition Problem We first graph the feasible set S for the problem. ✦ Graph the solution for the inequality considering only positive values for x and y: 100 200 300 x y 40 10 2400x y 40 10 2400x y (60, 0) (0, 240)
- 51. 200 100 Applied Example 2: A Nutrition Problem We first graph the feasible set S for the problem. ✦ Graph the solution for the inequality considering only positive values for x and y: 100 200 300 x y 10 15 2100x y 10 15 2100x y (210, 0) (0, 140)
- 52. 200 100 Applied Example 2: A Nutrition Problem We first graph the feasible set S for the problem. ✦ Graph the solution for the inequality considering only positive values for x and y: 100 200 300 x y 5 15 1500x y 5 15 1500x y (300, 0) (0, 100)
- 53. 200 100 Applied Example 2: A Nutrition Problem We first graph the feasible set S for the problem. ✦ Graph the intersection of the solutions to the inequalities, yielding the feasible set S. (Note that the feasible set S is unbounded) 100 200 300 x y S10 15 2100x y 40 10 2400x y 5 15 1500x y
- 54. 200 100 Applied Example 2: A Nutrition Problem Next, find the vertices of the feasible set S. ✦ The vertices are A(0, 240), B(30, 120), C(120, 60), and D(300, 0). 100 200 300 x y S10 15 2100x y 40 10 2400x y 5 15 1500x y C(120, 60) D(300, 0) A(0, 240) B(30, 120)
- 55. Applied Example 2: A Nutrition Problem Now, find the values of C at the vertices and tabulate them: 200 100 100 200 300 x y S10 15 2100x y 40 10 2400x y 5 15 1500x y C(120, 60) D(300, 0) A(0, 240) B(30, 120) Vertex C = 6x + 8y A(0, 240) 1920 B(30, 120) 1140 C(120, 60) 1200 D(300, 0) 1800
- 56. Applied Example 2: A Nutrition Problem Finally, identify the vertex with the lowest value for C: ✦ We can see that C is minimized at the vertex B(30, 120) and has a value of 1140. 200 100 100 200 300 x y S10 15 2100x y 40 10 2400x y 5 15 1500x y C(120, 60) D(300, 0) A(0, 240) Vertex C = 6x + 8y A(0, 240) 1920 B(30, 120) 1140 C(120, 60) 1200 D(300, 0) 1800 B(30, 120)
- 57. Applied Example 2: A Nutrition Problem Finally, identify the vertex with the lowest value for C: ✦ We can see that C is minimized at the vertex B(30, 120) and has a value of 1140. ✦ Recalling what the symbols x, y, and C represent, we conclude that the individual should purchase 30 brand-A pills and 120 brand-B pills at a minimum cost of $11.40.
- 58. 6.4 The Simplex Method: Standard Maximization Problems x y u v P Constant 1 0 3/5 –1/5 0 48 0 1 –1/5 2/5 0 84 0 0 9/25 7/25 1 148 4/5
- 59. The Simplex Method The simplex method is an iterative procedure. Beginning at a vertex of the feasible region S, each iteration brings us to another vertex of S with an improved value of the objective function. The iteration ends when the optimal solution is reached.
- 60. A Standard Linear Programming Problem A standard maximization problem is one in which 1. The objective function is to be maximized. 2. All the variables involved in the problem are nonnegative. 3. All other linear constraints may be written so that the expression involving the variables is less than or equal to a nonnegative constant.
- 61. Setting Up the Initial Simplex Tableau 1. Transform the system of linear inequalities into a system of linear equations by introducing slack variables. 2. Rewrite the objective function in the form where all the variables are on the left and the coefficient of P is +1. Write this equation below the equations in step 1. 3. Write the augmented matrix associated with this system of linear equations. 1 1 2 2 n nP c x c x c x 1 1 2 2 0n nc x c x c x P
- 62. Applied Example 1: A Production Problem Recall the production problem discussed in section 6.3, which required us to maximize the objective function subject to the system of inequalities This is a standard maximization problem and may be solved by the simplex method. Set up the initial simplex tableau for this linear programming problem. , 0x y 6 1.2 5 P x y P x y or equivalently, 3 300x y 2 180x y
- 63. Applied Example 1: A Production Problem Solution First, introduce the slack variables u and v into the inequalities and turn these into equations, getting Next, rewrite the objective function in the form 2 180 3 300 x y u x y v 3 300x y 2 180x y 6 0 5 x y P
- 64. Applied Example 1: A Production Problem Solution Placing the restated objective function below the system of equations of the constraints we get Thus, the initial tableau associated with this system is 2 180 3 300 6 0 5 x y u x y v x y P x y u v P Constant 2 1 1 0 0 180 1 3 0 1 0 300 –1 – 6/5 0 0 1 0
- 65. The Simplex Method 1. Set up the initial simplex tableau. 2. Determine whether the optimal solution has been reached by examining all entries in the last row to the left of the vertical line. a. If all the entries are nonnegative, the optimal solution has been reached. Proceed to step 4. b. If there are one or more negative entries, the optimal solution has not been reached. Proceed to step 3. 3. Perform the pivot operation. Return to step 2. 4. Determine the optimal solution(s).
- 66. Applied Example 1: A Production Problem Recall again the production problem discussed previously. We have already performed step 1 obtaining the initial simplex tableau: Now, complete the solution to the problem. x y u v P Constant 2 1 1 0 0 180 1 3 0 1 0 300 –1 – 6/5 0 0 1 0
- 67. Applied Example 1: A Production Problem Solution Step 2. Determine whether the optimal solution has been reached. ✦ Since there are negative entries in the last row of the tableau, the initial solution is not optimal. x y u v P Constant 2 1 1 0 0 180 1 3 0 1 0 300 –1 – 6/5 0 0 1 0
- 68. Applied Example 1: A Production Problem Solution Step 3. Perform the pivot operation. ✦ Since the entry – 6/5 is the most negative entry to the left of the vertical line in the last row of the tableau, the second column in the tableau is the pivot column. x y u v P Constant 2 1 1 0 0 180 1 3 0 1 0 300 –1 – 6/5 0 0 1 0
- 69. Applied Example 1: A Production Problem Solution Step 3. Perform the pivot operation. ✦ Divide each positive number of the pivot column into the corresponding entry in the column of constants and compare the ratios thus obtained. ✦ We see that the ratio 300/3 = 100 is less than the ratio 180/1 = 180, so row 2 is the pivot row. x y u v P Constant 2 1 1 0 0 180 1 3 0 1 0 300 –1 – 6/5 0 0 1 0 180 1 300 3 180 100
- 70. Applied Example 1: A Production Problem Solution Step 3. Perform the pivot operation. ✦ The entry 3 lying in the pivot column and the pivot row is the pivot element. x y u v P Constant 2 1 1 0 0 180 1 3 0 1 0 300 –1 – 6/5 0 0 1 0
- 71. Applied Example 1: A Production Problem Solution Step 3. Perform the pivot operation. ✦ Convert the pivot element into a 1. 1 23 R x y u v P Constant 2 1 1 0 0 180 1 3 0 1 0 300 –1 – 6/5 0 0 1 0
- 72. Applied Example 1: A Production Problem Solution Step 3. Perform the pivot operation. ✦ Convert the pivot element into a 1. 1 23 R x y u v P Constant 2 1 1 0 0 180 1/3 1 0 1/3 0 100 –1 – 6/5 0 0 1 0
- 73. Applied Example 1: A Production Problem Solution Step 3. Perform the pivot operation. ✦ Use elementary row operations to convert the pivot column into a unit column. 1 2 6 3 25 R R R R x y u v P Constant 2 1 1 0 0 180 1/3 1 0 1/3 0 100 –1 – 6/5 0 0 1 0
- 74. Applied Example 1: A Production Problem Solution Step 3. Perform the pivot operation. ✦ Use elementary row operations to convert the pivot column into a unit column. 1 2 6 3 25 R R R R x y u v P Constant 5/3 0 1 –1/3 0 80 1/3 1 0 1/3 0 100 –3/5 0 0 2/5 1 120
- 75. Applied Example 1: A Production Problem Solution Step 3. Perform the pivot operation. ✦ This completes an iteration. ✦ The last row of the tableau contains a negative number, so an optimal solution has not been reached. ✦ Therefore, we repeat the iteration step. x y u v P Constant 5/3 0 1 –1/3 0 80 1/3 1 0 1/3 0 100 –3/5 0 0 2/5 1 120
- 76. Applied Example 1: A Production Problem Solution Step 3. Perform the pivot operation again. ✦ Since the entry – 3/5 is the most negative entry to the left of the vertical line in the last row of the tableau, the first column in the tableau is now the pivot column. x y u v P Constant 5/3 0 1 –1/3 0 80 1/3 1 0 1/3 0 100 –3/5 0 0 2/5 1 120
- 77. Applied Example 1: A Production Problem Solution Step 3. Perform the pivot operation. ✦ Divide each positive number of the pivot column into the corresponding entry in the column of constants and compare the ratios thus obtained. ✦ We see that the ratio 80/(5/3) = 48 is less than the ratio 100/(1/3) = 300, so row 1 is the pivot row now. x y u v P Constant 5/3 0 1 –1/3 0 80 1/3 1 0 1/3 0 100 –3/5 0 0 2/5 1 120 80 5/3 100 1/3 48 300 Ratio
- 78. Applied Example 1: A Production Problem Solution Step 3. Perform the pivot operation. ✦ The entry 5/3 lying in the pivot column and the pivot row is the pivot element. x y u v P Constant 5/3 0 1 –1/3 0 80 1/3 1 0 1/3 0 100 –3/5 0 0 2/5 1 120
- 79. Applied Example 1: A Production Problem Solution Step 3. Perform the pivot operation. ✦ Convert the pivot element into a 1. x y u v P Constant 5/3 0 1 –1/3 0 80 1/3 1 0 1/3 0 100 –3/5 0 0 2/5 1 120 3 15 R
- 80. Applied Example 1: A Production Problem Solution Step 3. Perform the pivot operation. ✦ Convert the pivot element into a 1. x y u v P Constant 1 0 3/5 –1/5 0 48 1/3 1 0 1/3 0 100 –3/5 0 0 2/5 1 120 3 15 R
- 81. Applied Example 1: A Production Problem Solution Step 3. Perform the pivot operation. ✦ Use elementary row operations to convert the pivot column into a unit column. 1 2 13 3 3 15 R R R R x y u v P Constant 1 0 3/5 –1/5 0 48 1/3 1 0 1/3 0 100 –3/5 0 0 2/5 1 120
- 82. Applied Example 1: A Production Problem Solution Step 3. Perform the pivot operation. ✦ Use elementary row operations to convert the pivot column into a unit column. 1 2 13 3 3 15 R R R R x y u v P Constant 1 0 3/5 –1/5 0 48 0 1 –1/5 2/5 0 84 0 0 9/25 7/25 1 148 4/5
- 83. Applied Example 1: A Production Problem Solution Step 3. Perform the pivot operation. ✦ The last row of the tableau contains no negative numbers, so an optimal solution has been reached. x y u v P Constant 1 0 3/5 –1/5 0 48 0 1 –1/5 2/5 0 84 0 0 9/25 7/25 1 148 4/5
- 84. Applied Example 1: A Production Problem Solution Step 4. Determine the optimal solution. ✦ Locate the basic variables in the final tableau. In this case, the basic variables are x, y, and P. The optimal value for x is 48. The optimal value for y is 84. The optimal value for P is 148.8. ✦ Thus, the firm will maximize profits at $148.80 by producing 48 type-A souvenirs and 84 type-B souvenirs. This agrees with the results obtained in section 6.3. x y u v P Constant 1 0 3/5 –1/5 0 48 0 1 –1/5 2/5 0 84 0 0 9/25 7/25 1 148 4/5
- 85. 6.5 The Simplex Method: Standard Minimization Problems 3030 ––1/501/50 3/1003/100 xx 00 11 00 vv 450450 11/1011/10 ––3/203/20 ww 00 00 11 uu 1140114011120120 13/2513/25002/252/25 1/501/5000––1/501/50 ConstantConstantPPyy 3030 ––1/501/50 3/1003/100 xx 00 11 00 vv 450450 11/1011/10 ––3/203/20 ww 00 00 11 uu 1140114011120120 13/2513/25002/252/25 1/501/5000––1/501/50 ConstantConstantPPyy SolutionSolution for thefor the primal problemprimal problem
- 86. Minimization with Constraints In the last section we developed the simplex method to solve linear programming problems that satisfy three conditions: 1. The objective function is to be maximized. 2. All the variables involved are nonnegative. 3. Each linear constraint may be written so that the expression involving the variables is less than or equal to a nonnegative constant. We will now see how the simplex method can be used to solve minimization problems that meet the second and third conditions listed above.
- 87. Example Solve the following linear programming problem: This problem involves the minimization of the objective function and so is not a standard maximization problem. Note, however, that all the other conditions for a standard maximization hold true. 2 3Minimize C x y 5 4 32 2 10 , 0 subject to x y x y x y
- 88. Example We can use the simplex method to solve this problem by converting the objective function from minimizing C to its equivalent of maximizing P = – C. Thus, the restated linear programming problem is This problem can now be solved using the simplex method as discussed in section 6.4. 2 3Maximize P x y 5 4 32 2 10 , 0 subject to x y x y x y
- 89. Example Solution Step 1. Set up the initial simplex tableau. ✦ Turn the constraints into equations adding to them the slack variables u and v. Also rearrange the objective function and place it below the constraints: ✦ Write the coefficients of the system in a tableau: 5 4 32 2 10 2 3 0 x y u x y v x y P 2 3Maximize P x y x y u v P Constant 5 4 1 0 0 32 1 2 0 1 0 10 –2 –3 0 0 1 0
- 90. Example Solution Step 2. Determine whether the optimal solution has been reached. ✦ Since there are negative entries in the last row of the tableau, the initial solution is not optimal. x y u v P Constant 5 4 1 0 0 32 1 2 0 1 0 10 –2 –3 0 0 1 0
- 91. Example Solution Step 3. Perform the pivot operation. ✦ Since the entry – 3 is the most negative entry to the left of the vertical line in the last row of the tableau, the second column in the tableau is the pivot column. 2 3Maximize P x y x y u v P Constant 5 4 1 0 0 32 1 2 0 1 0 10 –2 –3 0 0 1 0
- 92. Example Solution Step 3. Perform the pivot operation. ✦ Divide each positive number of the pivot column into the corresponding entry in the column of constants and compare the ratios thus obtained. ✦ We see that the ratio 10/2 = 5 is less than the ratio 32/4 = 8, so row 2 is the pivot row. 2 3Maximize P x y 32 4 10 2 8 5 x y u v P Constant 5 4 1 0 0 32 1 2 0 1 0 10 –2 –3 0 0 1 0 Ratio
- 93. Example Solution Step 3. Perform the pivot operation. ✦ The entry 2 lying in the pivot column and the pivot row is the pivot element. 2 3Maximize P x y x y u v P Constant 5 4 1 0 0 32 1 2 0 1 0 10 –2 –3 0 0 1 0
- 94. Example Solution Step 3. Perform the pivot operation. ✦ Convert the pivot element into a 1. 2 3Maximize P x y x y u v P Constant 5 4 1 0 0 32 1 2 0 1 0 10 –2 –3 0 0 1 0 1 22 R
- 95. Example Solution Step 3. Perform the pivot operation. ✦ Convert the pivot element into a 1. 2 3Maximize P x y x y u v P Constant 5 4 1 0 0 32 1/2 1 0 1/2 0 5 –2 –3 0 0 1 0 1 22 R
- 96. Example Solution Step 3. Perform the pivot operation. ✦ Use elementary row operations to convert the pivot column into a unit column. 2 3Maximize P x y 1 2 3 2 4 3 R R R R x y u v P Constant 5 4 1 0 0 32 1/2 1 0 1/2 0 5 –2 –3 0 0 1 0
- 97. Example Solution Step 3. Perform the pivot operation. ✦ Use elementary row operations to convert the pivot column into a unit column. 2 3Maximize P x y 1 2 3 2 4 3 R R R R x y u v P Constant 3 0 1 –2 0 12 1/2 1 0 1/2 0 5 –1/2 0 0 3/2 1 15
- 98. Example Solution Step 3. Perform the pivot operation. ✦ This completes an iteration. ✦ The last row of the tableau contains a negative number, so an optimal solution has not been reached. ✦ Therefore, we repeat the iteration step. 2 3Maximize P x y x y u v P Constant 3 0 1 –2 0 12 1/2 1 0 1/2 0 5 –1/2 0 0 3/2 1 15
- 99. Example Solution Step 3. Perform the pivot operation. ✦ Since the entry –1/2 is the most negative entry to the left of the vertical line in the last row of the tableau, the first column in the tableau is now the pivot column. 2 3Maximize P x y x y u v P Constant 3 0 1 –2 0 12 1/2 1 0 1/2 0 5 –1/2 0 0 3/2 1 15
- 100. Example Solution Step 3. Perform the pivot operation. ✦ Divide each positive number of the pivot column into the corresponding entry in the column of constants and compare the ratios thus obtained. ✦ We see that the ratio 12/3 = 4 is less than the ratio 5/(1/2) = 10, so row 1 is now the pivot row. 2 3Maximize P x y x y u v P Constant 3 0 1 –2 0 12 1/2 1 0 1/2 0 5 –1/2 0 0 3/2 1 15 12 3 5 1/2 4 10
- 101. Example Solution Step 3. Perform the pivot operation. ✦ The entry 3 lying in the pivot column and the pivot row is the pivot element. x y u v P Constant 3 0 1 –2 0 12 1/2 1 0 1/2 0 5 –1/2 0 0 3/2 1 15
- 102. Example Solution Step 3. Perform the pivot operation. ✦ Convert the pivot element into a 1. x y u v P Constant 3 0 1 –2 0 12 1/2 1 0 1/2 0 5 –1/2 0 0 3/2 1 15 1 13 R
- 103. Example Solution Step 3. Perform the pivot operation. ✦ Convert the pivot element into a 1. x y u v P Constant 1 0 1/3 –2/3 0 4 1/2 1 0 1/2 0 5 –1/2 0 0 3/2 1 15 1 13 R
- 104. Example Solution Step 3. Perform the pivot operation. ✦ Use elementary row operations to convert the pivot column into a unit column. 1 2 12 1 3 12 R R R R x y u v P Constant 1 0 1/3 –2/3 0 4 1/2 1 0 1/2 0 5 –1/2 0 0 3/2 1 15
- 105. Example Solution Step 3. Perform the pivot operation. ✦ Use elementary row operations to convert the pivot column into a unit column. 1 2 12 1 3 12 R R R R x y u v P Constant 1 0 1/3 –2/3 0 4 0 1 –1/6 5/6 0 3 0 0 1/6 7/6 1 17
- 106. Example Solution Step 3. Perform the pivot operation. ✦ The last row of the tableau contains no negative numbers, so an optimal solution has been reached. x y u v P Constant 1 0 1/3 –2/3 0 4 0 1 –1/6 5/6 0 3 0 0 1/6 7/6 1 17
- 107. Example Solution Step 4. Determine the optimal solution. ✦ Locate the basic variables in the final tableau. In this case, the basic variables are x, y, and P. The optimal value for x is 4. The optimal value for y is 3. The optimal value for P is 17, which means that the minimized value for C is –17. x y u v P Constant 1 0 1/3 –2/3 0 4 0 1 –1/6 5/6 0 3 0 0 1/6 7/6 1 17
- 108. The Dual Problem Another special class of linear programming problems we encounter in practical applications is characterized by the following conditions: 1. The objective function is to be minimized. 2. All the variables involved are nonnegative. 3. All other linear constraints may be written so that the expression involving the variables is greater than or equal to a nonnegative constant. Such problems are called standard minimization problems.
- 109. The Dual Problem In solving this kind of linear programming problem, it helps to note that each maximization problem is associated with a minimization problem, and vice versa. The given problem is called the primal problem, and the related problem is called the dual problem.
- 110. Example Write the dual problem associated with this problem: We first write down a tableau for the primal problem: 6 8Minimize C x y 40 10 2400 10 15 2100 5 15 1500 , 0 subject to x y x y x y x y x y Constant 40 10 2400 10 15 2100 5 15 1500 6 8 Primal Problem
- 111. Example Next, we interchange the columns and rows of the tableau and head the three columns of the resulting array with the three variables u, v, and w, obtaining x y Constant 40 10 2400 10 15 2100 5 15 1500 6 8 u v w Constant 40 10 5 6 10 15 15 8 2400 2100 1500
- 112. Example Consider the resulting tableau as if it were the initial simplex tableau for a standard maximization problem. From it we can reconstruct the required dual problem: u v w Constant 40 10 5 6 10 15 15 8 2400 2100 1500 2400 2100 1500Maximize P u v w 40 10 5 6 10 15 15 8 , , 0 subject to u v w u v w u v w Dual Problem
- 113. Theorem 1 The Fundamental Theorem of Duality A primal problem has a solution if and only if the corresponding dual problem has a solution. Furthermore, if a solution exists, then: a. The objective functions of both the primal and the dual problem attain the same optimal value. b. The optimal solution to the primal problem appears under the slack variables in the last row of the final simplex tableau associated with the dual problem.
- 114. Example Complete the solution of the problem from our last example: 2400 2100 1500Maximize P u v w 40 10 5 6 10 15 15 8 , , 0 subject to u v w u v w u v w Dual Problem
- 115. Example Solution The dual problem associated with the given primal problem is a standard maximization problem. Thus, we can proceed with the simplex method. First, we introduce to the system of equations the slack variables x and y, and restate the inequalities as equations, obtaining 40 10 5 6 10 15 15 8 2400 2100 1500 0 u v w x u v w y u v w P
- 116. Example Solution Next, we transcribe the coefficients of the system of equations into an initial simplex tableau: 40 10 5 6 10 15 15 8 2400 2100 1500 0 u v w x u v w y u v w P u v w x y P Constant 40 10 5 1 0 0 6 10 15 15 0 1 0 8 –2400 –2100 –1500 0 0 1 0
- 117. Example Solution Continue with the simplex iterative method until a final tableau is obtained with the solution for the problem: The fundamental theorem of duality tells us that the solution to the primal problem is x = 30 and y = 120, with a minimum value for C of 1140. u v w x y P Constant 1 0 –3/20 3/100 –1/50 0 1/50 0 1 11/10 –1/50 2/25 0 13/25 0 0 450 30 120 1 1140 Solution for the primal problem
- 118. End of Chapter