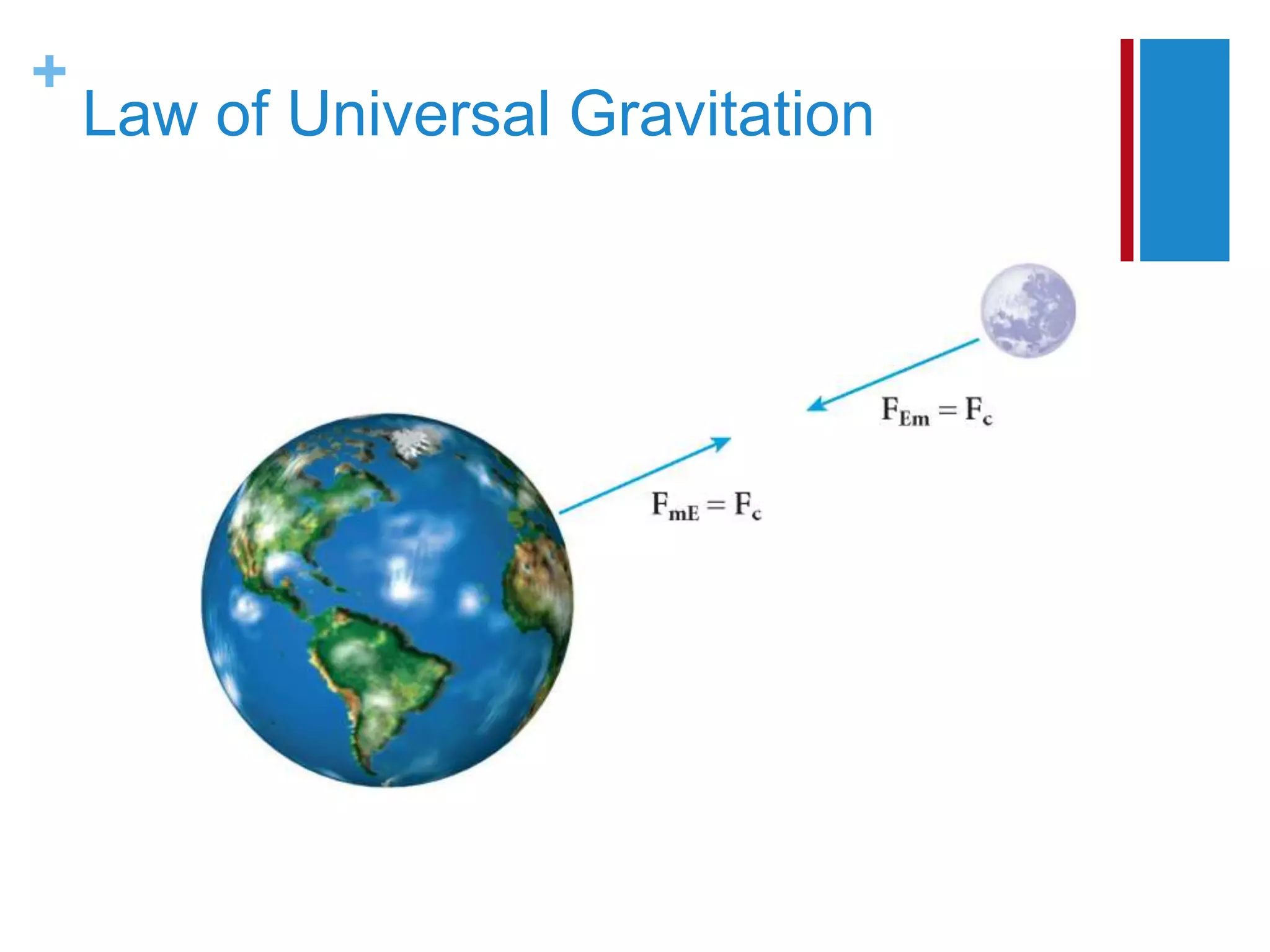
The document summarizes key concepts about circular motion, Newton's law of universal gravitation, motion in space, and weightlessness. It discusses centripetal acceleration and force, Kepler's laws of planetary motion, and how apparent weightlessness occurs in falling elevators and orbiting spacecraft due to inertia rather than a lack of gravitational force. Examples and equations are provided to calculate values like tangential speed, centripetal force, gravitational force, and planetary orbital properties.