Correlation

Хамаарлыг судлах аргууд

Хамаарал гэж юу вэ?
 Аливаа нэг зүйл нөгөөдөө нөлөөлж
байдаг. Өөрөөр хэлбэл нэг зүйлийн
утга нөгөөгөөс хамаардаг.
Тодорхойлолт: Хамаарал гэдэг нь
үзэгдэл хоорондын нөлөөллийн
хэлнэ.

Хамаарлын төрөл
Хамаарал
Энгийн Нийлмэл

Хамаарал тухай ойлголт
X Y
Х-хамаарах хувьсагч
Y-үл хамаарах хувьсагч

Хамаарлын судлах зүйл
Чиглэл
Хүч
Хэлбэр

Хамаарлын чиглэл
Чиглэл
Шууд /ижил/ Урвуу
X Y X Y

Хамаарлын хэлбэр
Хэлбэр
Шулуун шугаман Муруй шугаман

Корреляци хамаарал
(Correlation)

Correlation
 Түлхүүр үг:
a) Цэгэн диаграмм
b) Пирсоны Корреляцийн коэффициент
c) Спирмений Рангийн Корреляцын
коэффициент
d) Хамгийн бага квадратын арга

Корреляци
Хоёр тоон хүчин зүйл хэр их
шугаман хамааралтай байна
вэ? гэдгийг илтгэдэг.

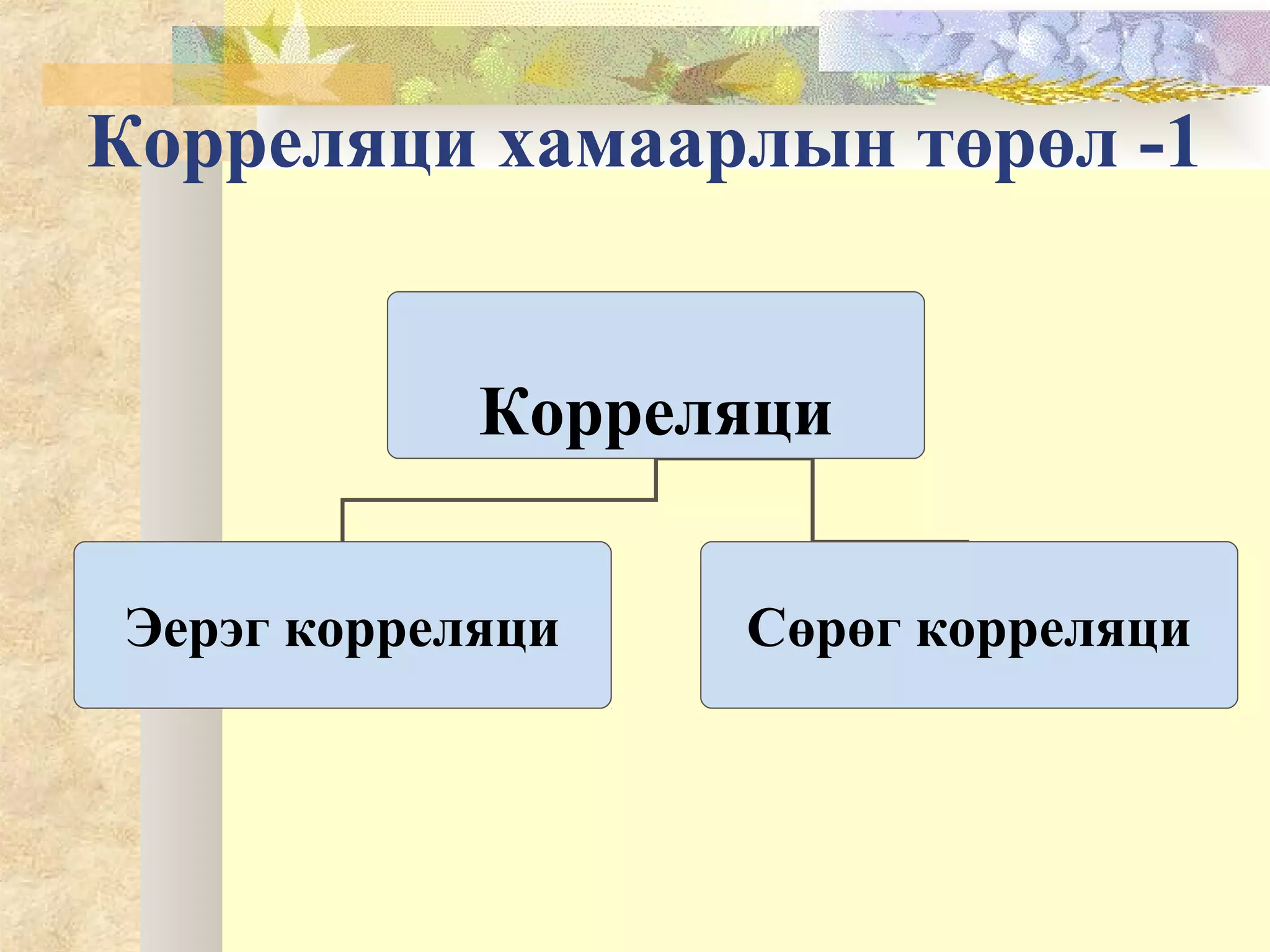
Корреляци хамаарлын төрөл -1
Корреляци
Эерэг корреляци Сөрөг корреляци

 Эерэг корреляци: Нэг хувьсагчын утга
нэмэгдэхэд нөгөө хувьсагчын утга дагаад
нэмэгддэг.
Жишээ: Өндөр & Жин , Ор хоног &
Зардал
 Сөрөг корреляци: Нэг хувьсагчын утга
нэмэгдэхэд нөгөө хувьсагчын утга буурдаг.
Жишээ: Өндөр & Жин , Ор хоног & Зардал

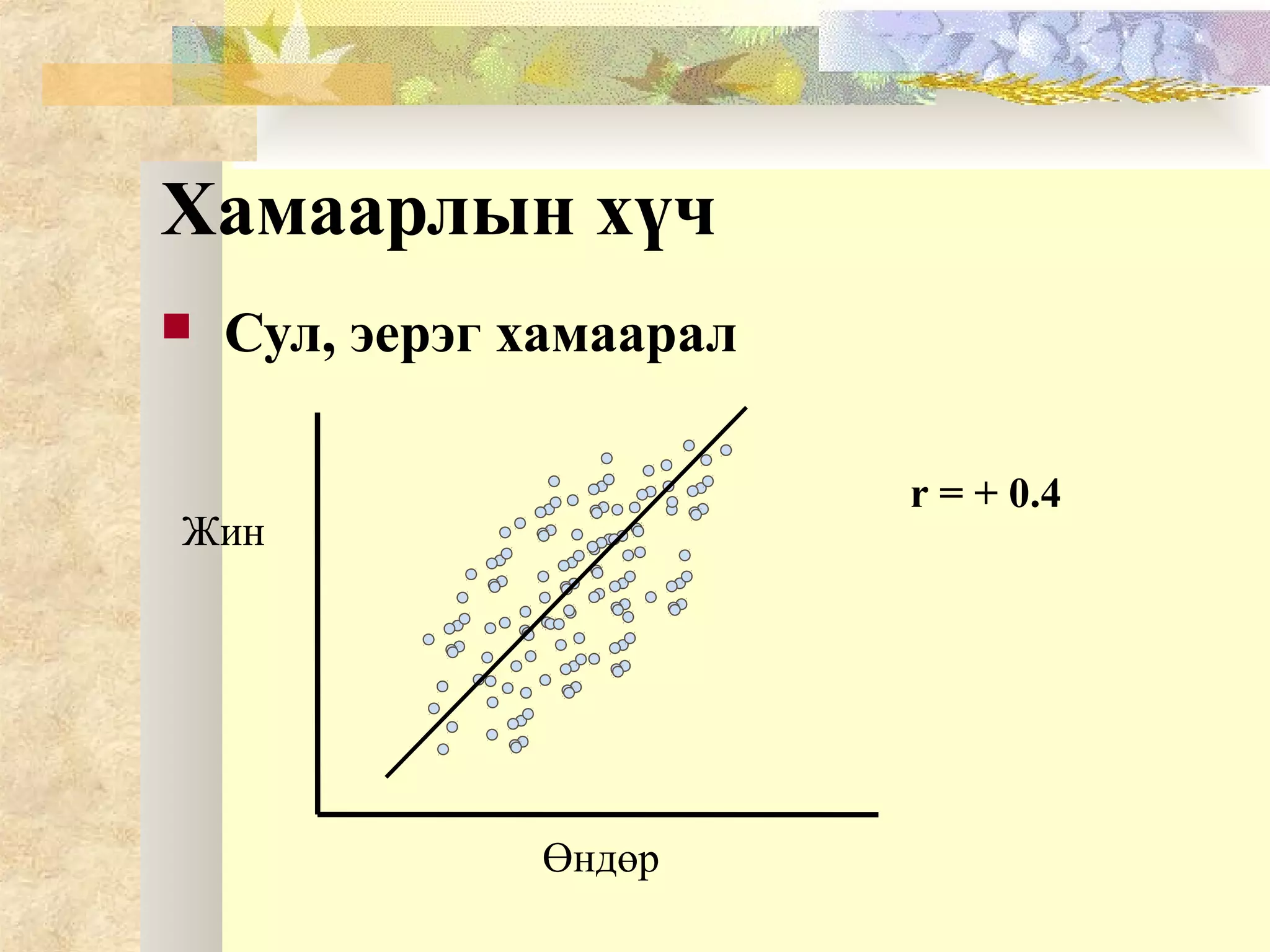
Хамаарлын чиглэл
 Эерэг хамаарал – Хувьсагчууд эерэг чиглэлтэй.
X - өсөхөд, Y өсдөг
X буурхад, Y буурдаг
Жишээ: Биеийн өндөр буурхад ----> Биеийн жин
буурдаг
 Сөрөг хамаарал – Хувьсагчууд эсрэг чиглэлтэй.
X өсөхөд, Y буурдаг
X буурхад, Y өсдөг
Жишээ: TV-үзэх хугацаа ----> Хичээл давтах
хугацаа
Indicated by
sign; (+) or (-).

Бусад жишээ:
 Эерэг хамаарал:Эерэг хамаарал:
 Усны хэрэглээ ба
температур.
 Суралцах хугацаа ба
Анги.
 Сөрөг хамааралСөрөг хамаарал:
 Архины хэрэглээ ба
жолоодох ур чадвар.
 Үнэ ба барааны тоо

Корреляци хамаарлын төрөл
-2
Корреляци
Энгийн Нийлмэл
Хэсэгчилсэн Нийлбэр

 Энгийн корреляци: Зөвхөн 2 тоон хувьсагын
хувьд тооцно.
 Нийлмэл корреляци: 3 буюу түүнээс дээш
тооны хувьсагчтай үед тооцно.
 Хэсгийн корреляци: Корреляцийн хос
коэффициентууд нь үр дүнгийн шинж тэмдэгт
нөлөөлөх хүчин зүйлээс гадна тооцоонд
ороогүй бусад хүчин зүйлийн нөлөөг
харуулдаг.
 Нийлбэр корреляци: хамаарах хувьсагчын
утга өндөр хэлбэлзэлтэй үед тооцно. Хэвийн
тархалттай биш байж болно.

Корреляци хамаарлын төрөл
-3
Корреляци
Шугаман Шугаман бус

 Шугаман корреляци: Нэг хувьсагын утга
өөрчлөгдөхөд нөгөө хувьсагчын утга дагаад
өөрчлөгддөг. Өөрөөр хэлбэл хувьсагчууд
хоорондоо тодорхой харьцаатайгаар харилцан бие
биедээ нөлөөлдөг.
Жишээ: X = 15, 16, 17, 18, 19, 20, 21, 22,
Y = 1,5 1,7 1,9 2,1 2,3 2,5 2,7 2,9
Y = 0.1x+0
 Шугаман бус корреляци: Хувьсагчдын
хоорондын тодорхой харьцаа байхгүй.

Корреляци хамаарлыг
тодорхойлох
 Цэгэн диаграмм
 График арга
 Пирсоны Корреляци
коэффициеэт
 Хамгийн бага квадратын арга

Цэгэн диаграмм
(Scatter Diagram)
 Цэгэн диаграмм нь ажиглалтын үр
дүнг тэгш өнцөгтийн кординатын
системд байгуулдаг.
 Өөрөөр хэлбэл X & Y хос
цэгүүдээр хамаарлыг
тодорхойлдог.

Эерэг корреляци
Өндөр
Жин
Height
of A
Weight
of A
Height
of B
Weight
of B
Шугаман
хамаарал

Хамаарлын хүч
 Хүчтэй, эерэг хамаарал
Өндар
Жин
r = +0.80

 Сул, эерэг хамаарал
Өндөр
Жин
r = + 0.4

 Сөрөг корреляци
Шалгалтын оноо
7 хоногт
TV үздэг
цаг
r = -1.0

 Хүчтэй, сөрөг хамаарал
Шалгалтын оноо
7 хоногт
TV үздэг
цаг
r = -0.80

 Сул, сөрөг хамаарал
Жин
Гутлын
разимер
r = - 0.2

 Хамааралгүй (Хөндөлн шугам)
Өндөр
IQ
r = 0.0

Хамаарлын хүч (r)
r = +.80 r = +.60
r = +.40 r = +.20

Цэгэн диаграммын давуу тал
 Хамгийн энгийн хялбар арга
 Алслагдсан утга (extreme value)
нөлөөлөхгүй
 2 хувьсагчын хоорондын хамаарлыг
тооцох хамгийн эхний үе шат

Цэгэн диаграмм сул тал
Хамаарлын хүчийг нарийвчлалтай
тооцдоггүй

Пирсоны Корреляцийн
 Тэмдэглэгээ ‘r’.
 Корреляци коэффициент( -1≤ r ≥+1)
 Ажиглалын үр дүнгийн (x & y )
хоорондын хамаарлын хүчийг
илтгэнэ.

Пирсоны Корреляцийн
 Түүврийн дундаж мэдэгдэж байгаа:
r(x, y)= Σxy /√ Σx² Σy²
 Түүврийн дундаж мэдэгдэхгүй байгаа:
r = N Σdxdy - Σdx Σdy
√N Σdx²-(Σdx)² √N Σdy²-(Σdy)²

Корреляцийн коэффициент
(r)
 r = +1, Хүчтэй , эерэг хамааралтай
байна.
 r = -1, Хүчтэй , сөрөг хамааралтай
байна.
 r = 0, Огт хамааралгүй байна.

Корреляци хамаарлын тухай
таамаглал шалгах
 Хоёр хувьсагчын хоорондох холбоо
хамаарлыг шалгадаг. (X,Y) хос үр дүн
бүхий цэгүүдээр (цэгэн диаграмм)
шугаман хамаарлыг харж болно.
 Хоёр хувьсагчын хоорондох
нөлөөллийн хувь хэмжээ, хүчийг
хэмжинэ.

Давуу тал
 Юмсын хоорондох нөлөөллийн
хэмждэг.
 Хамаарлын чиглэлийг
тодорхойлдог.

 Үргэлж шугаман хамаарал
шалгадаг
 Корреляцийн коэффициент r
хэрэглээ их.
 Алслагдсан утга нөлөөлөхгүй.
 Юмсын цаг хугацаан дахь
өөрчлөлтийг илтгэдэг

Детерминацийн коэффициент
 Үр дүнгийн (Y) нийт өөрчлөлтөнд (X)
шинж тэмдгийн өөрчлөлт хэрхэн
нөлөөлж байгааг харуулдаг.
 Детерминацийн коэффициент = R= r2
 Тооцох: r = 0.9, r2
= 0.81 нярайн
жингийн өөрчлөлтийн 81% нь
жирэмсний 7 хоногоос хамаарч байна.

Детерминаци коэффициент: Жишээ
 Бодолт:
Хэрвээ r = 0.60 r2
= 0.36 -----(1)
r = 0.30 r2
= 0.09 -----(2)
Тохиолдолд – 1
Хамаарлын хувь 36%-тай буюу нөлөөлөл
өндөр байна.
Тохиолдол – 2
Хамаарлын хувь 9%-тай буюу нөлөөлөл
бага байна.

Correlation

More Related Content

What's hot

Viewers also liked

Similar to Correlation

Correlation