Correlation, other correlation

Корреляци ба регрессийн
анализ
Эпидемиологи Биостатистикийн тэнхим
Нийгмийн Эрүүл Мэндийн Сургууль

Агуулга
• Энгийн корреляцийг тооцох, тайлбарлах
• Ач холбогдолтой эсэхийг шалгах
• Энгийн шугаман регрессийг тооцох
тайлбарлах
• Регрессийн урьдач нөхцөлүүд
• Регрессийн загвар ач холбогдолтой эсэхийг
тодорхойлох

Агуулга
(үргэлжлэл)

• Регрессийн коэффициетүүдийн итгэх
интервал
• Шугаман бус хамаарал

КОРРЕЛЯЦИЙН АНАЛИЗ

Нэр томъёо

Y хувьсагч Х хувьсагч

Хамааран хувьсагч Үл хамааран хувьсагч
Тайлбарлуулагч хувьсагч Тайлбарлагч хувьсагч
Үр дүнгийн хувьсагч Хүчин зүйлийн хувьсагч
....... .......

Ангилал 1.

Корреляци

Эерэг корреляци Сөрөг корреляци

Жин, систолын даралт Архины хэрэглээ , жолоодлогын
чадвар

Ангилал 2.

Корреляци

Олон хүчин
Энгийн зүйлийн

Хэсгийн Нийлбэр

Ангилал 3.

Корреляци

Шугаман Шугаман бус

Цэгэн диаграм ба Корреляци

• Цэгэн диаграм нь хоёр хувьсагчийн
хоорондох хамаарлыг үзүүлдэг.
• Корреляцийн шинжилгээ нь шугаман
хамаарлыг шинжилдэг.
– Нас болон систолын даралт
– Жин болон диастолын даралт

Жишээ
Шугаман хамаарал Шугаман бус хамаарал

y y

x x

y y

x x

Жишээ
Хүчтэй хамаарал Сул хамаарал

y y

x x

y y

x x

Жишээ
Хамааралгүй

y

x

y

x

Корреляцийн коэф

• ρ (rho) эх олонлогийн корреляцийн
коэф
• r нь түүврийн корреляцийн коэфф,
ρ-г үнэлэхэд хэрэглэдэг.

Авах утгууд
• -1 ба 1
• -1 ойртох тусам хүчтэй сөрөг
хамааралтай
• 1 ойртох тусам хүчтэй эерэг
• 0 ойртох тусам сул хамааралтай

Жишээлбэл

y y y

x x x
r = -1 r = -.6 r=0
y y

x x
r = +.3 r = +1

Хүчийг үнэлэх
• 0.00-0.20 - маш сул
• 0.21-0.40 - сул
• 0.41-0.60 - дундаж
• 0.61-0.80 - хүчтэй
• 0.81-1.00 - маш хүчтэй

Корреляцийн коэф-г тооцох
Түүврийн корреляци:

r
 ( x  x)(y  y)
[ ( x  x ) ][ ( y  y ) ]
2 2

Эквивалент :

n xy   x  y
r
[n(  x )  (  x ) ][n(  y )  (  y ) ]
2 2 2 2

Жишээ
Модны Их
өндөр биеийн
диаметр
y x xy y2 x2
35 8 280 1225 64
49 9 441 2401 81
27 7 189 729 49
33 6 198 1089 36
60 13 780 3600 169
21 7 147 441 49
45 11 495 2025 121
51 12 612 2601 144
=321 =73 =314 =14111 =713
2

Жишээ (үргэлжлэл)

Модны n xy   x  y
өндөр, r
y 70 [n(  x 2 )  (  x) 2 ][n(  y 2 )  (  y)2 ]
60

8(3142)  (73)(321)
50 
40
[8(713)  (73) 2 ][8(14111)  (321) 2 ]

 0.886
30

20

10

0
r = 0.886 → хүчтэй эерэг
0 2 4 6 8 10 12 14
Их биеийн диаметр, x

Excel ашиглах
Excel Корреляци тооцохдоо
Tools / data analysis / correlation…
Их биеийн
Модны өндөр диаметр
Модны өндөр 1
Их биеийн
диаметр 0.886231 1

Хувьсагч хоорондын хамаарал

Ач холбогдлыг шалгах
• Таамаглалууд
H0: ρ = 0 (хамааралгүй)
HA: ρ ≠ 0 (хамааралтай)

• Тестийн статистик
r
t (n – 2 чөлөөний зэрэг бүхий)
1 r 2

n2

Жишээ
H0: ρ = 0 (хамааралгүй)
H1: ρ ≠ 0 (хамааралтай)
 =.05 , df = 8 - 2 = 6
r .886
t   4.68
1 r 2 1  .886 2
n2 82

Жишээ

r .886 Шийдвэр :
t   4.68
1 r 2 1  .886 2 H0 няцаах

n2 82 Дүгнэлт:
Шугаман
d.f. = 8-2 = 6
хамааралтай,
5%-н ач
/2=.025 /2=.025
холбогдлын
түвшинд
няцаана H0 Няцаахгүй H0 няцаана H0
-tα/2 tα/2
0
-2.4469 2.4469
4.68

Бусад корреляцийн коэф
• Дараалсан хувьсагчид
– Спийрмений ρ эсвэл Кендалын Тау
• Дихитом хувьсагч (интервал/харьцаа)
– Цэгэн бисериал r (тасралттай)
– Бисериал r (тасралтгүй)
• Хоёр дихитом хувьсагч
– Phi коэффициент

Цэгэн бисериал r
• Үл хамаарах хувьсагч нь бодит дихитом
(2 категори)
• Хамааран хувьсагч нь интервал,
тасралтгүй
Жишээ
Үл хамаарах хувьсагч Хамааран хувьсагч
Эрүүл, өвчтэй холестрин
Эрэгтэй, эмэгтэй Цалин
........... ............

Бисериал r
• Үл хамаарах хувьсагч нь үүсмэл
дихитом (2 категори)
• Хамааран хувьсагч нь интервал,
тасралтгүй
Жишээ
Тарган, туранхай Холестрин
Даралт ихсэлттэй, хэвийн Цалин

........... ............

Phi корреляци
• Үл хамааран, хамааран хувьсагчид
бодит дихитом (2 категори) байна.

Жишээ
Тамхи (тийм, үгүй) Архи (тийм,үгүй)
Эрэгтэй эмэгтэй Профессор, профессор биш

........... ............

Спийрмений ρ, Кендаллын tau
• Үл хамааран, хамааран хувьсагчид
дараалсан байна.

– n > 20 бол Спийрмений ρ
– n < 20 бол Кендаллын tau
Жишээ
Насны бүлэг Боловсролын түвшин
Анги , дамжаа Дүн (A B C D F)
........... ............

Хэсгийн корреляци
• X ба Y-н корреляцид 3-дагч хувьсагчийн
нөлөөг засварлах

Хэсгийн корреляци

Нийлбэр корреляци

X2
X1 X3
Y

РЕГРЕССИЙН АНАЛИЗ

Энгийн регрессийн загвар

• Зөвхөн нэг үл хамаарах
хувьсагч, x
• х ба у хамаарлыг шугаман
функцээр тайлбарладаг.
• Х өөрчлөлтөөр У-н өөрчлөлтийг
тайлбарладаг.

Регрессийн загварын төрлүүд
Эерэг шугаман хамаарал Шугаман биш хамаарал

Сөрөг шугаман хамаарал Хамааралгүй

Эх олонлогийн шугаман
регресс
Эх олонлогийн регрессийн загвар:
Налалтын Үл хамаарах
тогтмол алдаа
коэфф хувьсагч
Хамааран

y  β0  β1x  ε
хувьсагч

Шугаман компонент Алдааны компонент

Шугаман регрессийн урьдач
нөхцөлүүд
• Алдаа (ε) үл хамаарах байна.
• Алдаа нь хэвийн тархалттай.
• Алдаа нь тогтмол дисперстэй.
• Х хувьсагч У-ээс шугаман хамаарна.

Эх олонлогийн шугаман
регресс (үргэлжлэл)

y y  β0  β1x  ε
Y-н бодит
утгууд

εi Налалт = β1
Y-н таамагласан
утгууд алдаа

тогтмол = β0

xi x

Регрессийн загварын үнэлгээ
Түүврийн регрессийн шулуунаар эх олонлогийн
шулуунаар төсөөлдөг.

Үнэлэгдсэн Үнэлсэн налалт
Үнэлэгдсэн (эсвэл
тогтмол
таамагласан) yтга

Үл хамаарах

y i  b 0  b1x
ˆ хувьсагч

Алдааны дундаж 0 байна.

Хамгийн бага квадратын арга

• b0 ба b1 -г олохдоо алдаануудын кв-г
минимумчилдаг.

 e   (y y
2
ˆ )2

  (y  (b
0  b1x)) 2

Тэнцэтгэл
• b1 ба b0 олох:

b1 
 ( x  x )( y  y )
 (x  x) 2

Эквивалент:
ба
 xy   x y
b1  n b0  y  b1 x
( x ) 2
 x2 
n

Налалт, тогтмол утгуудыг
тайлбарлах
• b0 нь х-н утга 0 байх үеийн у-н
дундаж

• b1 нь х-н нэгж өөрчлөлтөд
харгалзах у-н дундаж өөрчлөлт

Жишээ
(y) (x)

245 1400
312 1600
279 1700
308 1875
199 1100
219 1550
405 2350
324 2450
319 1425
255 1700

Excel ашиглах
• Tools / Data Analysis /
Regression

Excel үр дүн
Regression Statistics
Multiple R 0.76211
R Square 0.58082
Регрессийн тэгшитгэл:
y  98.24833 0.10977(x)
Adjusted R Square 0.52842
Standard Error 41.33032
Observations 10

ANOVA
df SS MS F Significance F

Regression 1 18934.9348 18934.9348 11.0848 0.01039

Residual 8 13665.5652 1708.1957
Total 9 32600.5000

Coefficients Standard Error t Stat P-value Lower 95% Upper 95%

Intercept 98.24833 58.03348 1.69296 0.12892 -35.57720 232.07386

Х 0.10977 0.03297 3.32938 0.01039 0.03374 0.18580

График
• Цэгэн диаграм ба регрессийн
шулуун

Налалт
= 0.10977

тогтмол
= 98.248

y  98.24833 0.10977(x)

Налалтын коэф-г
тайлбарлах, b1
y  98.24833 0.10977(x)

• Х нэг нэгжээр өсөхөд у дундажаар
0.1097 дахин өснө.

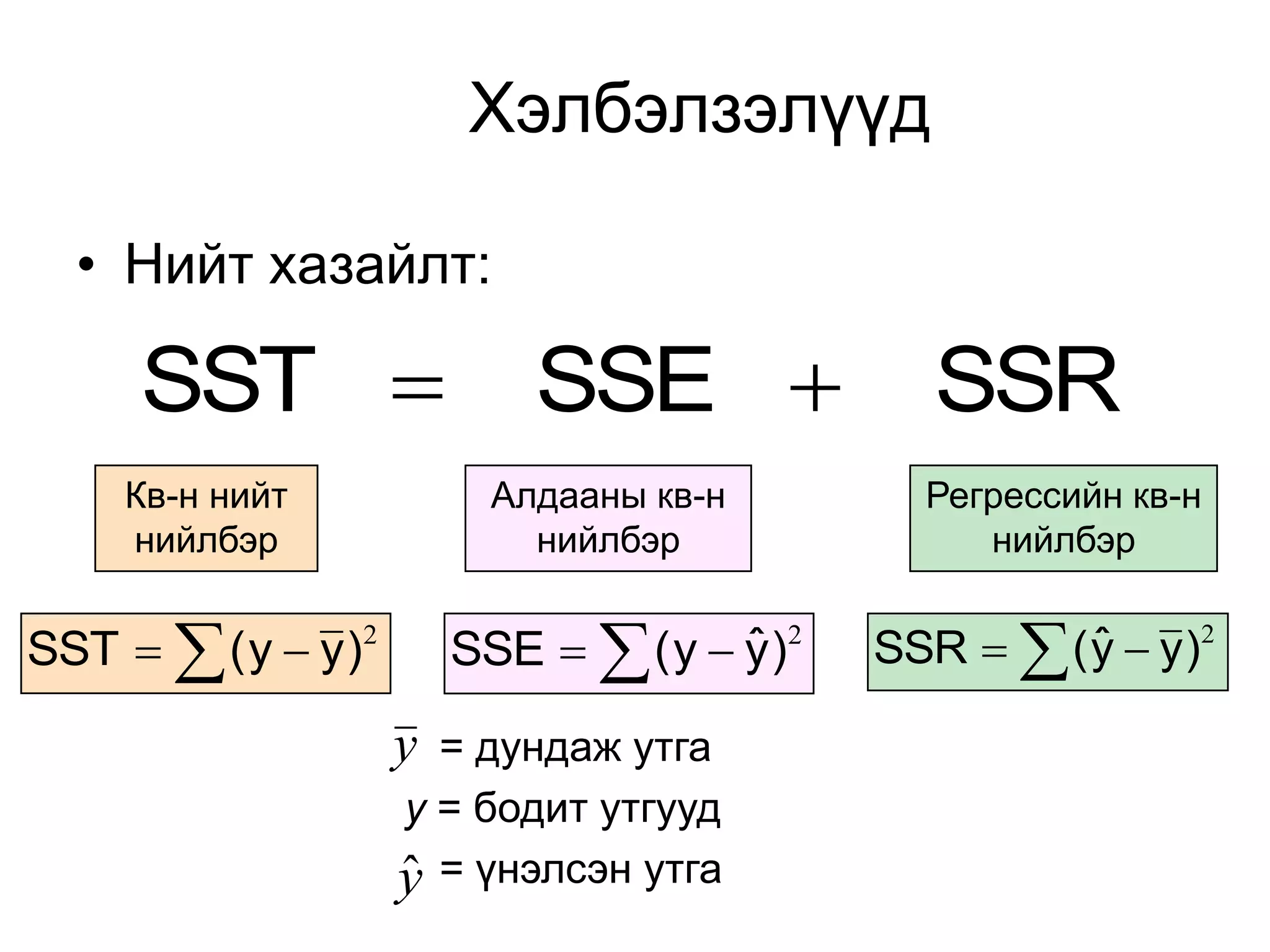
Хэлбэлзэлүүд

• Нийт хазайлт:

SST  SSE  SSR
Кв-н нийт Алдааны кв-н Регрессийн кв-н
нийлбэр нийлбэр нийлбэр

SST   ( y  y )2 SSE   ( y  y )2
ˆ SSR   ( y  y )2
ˆ

y = дундаж утга
y = бодит утгууд
ˆ
y = үнэлсэн утга

Хэлбэлзлүүд
y
yi 
 2
SSE = (yi - yi ) y
_
SST = (yi - y)2

y  _2
_ SSR = (yi - y) _
y y

Xi x

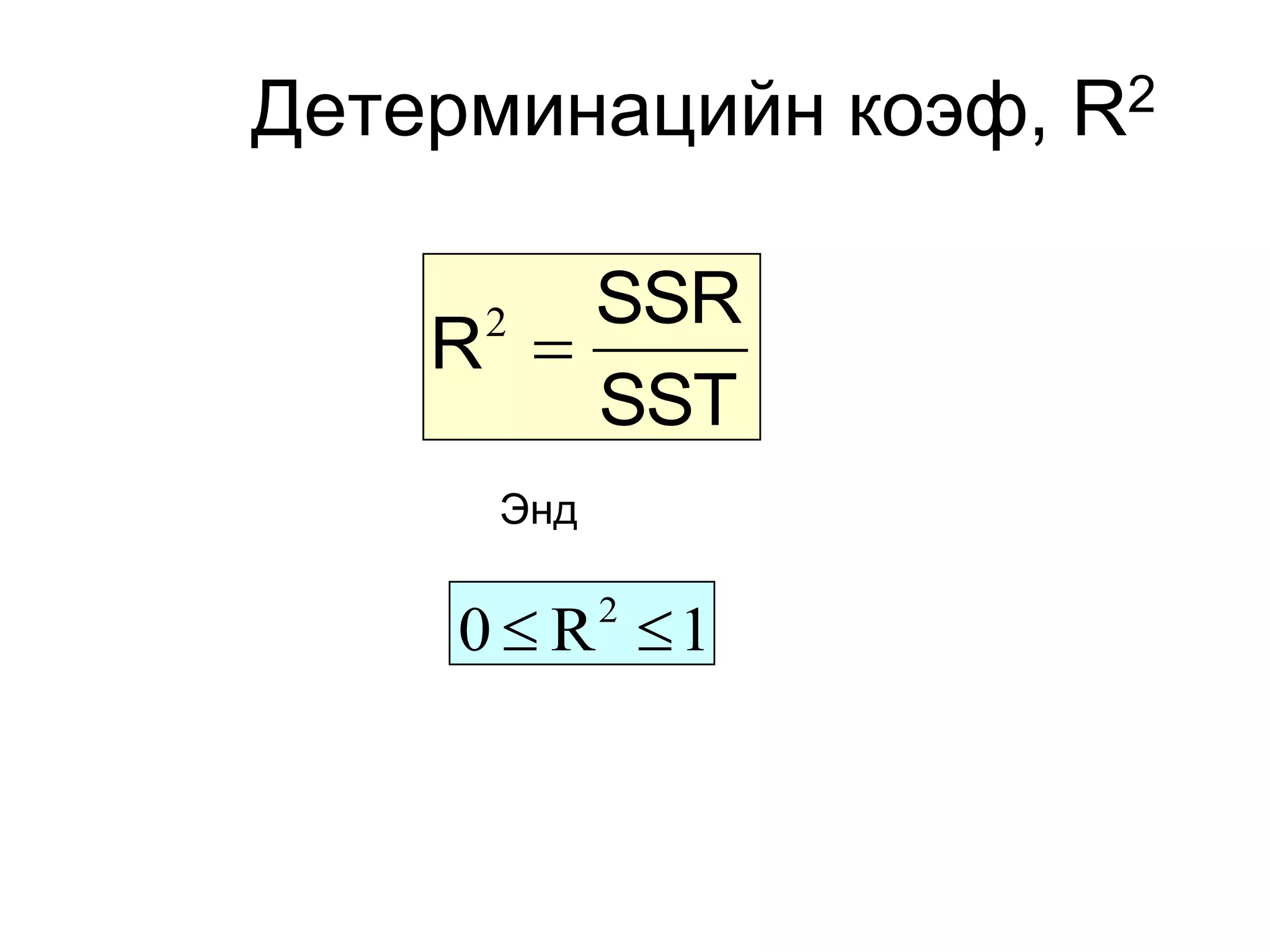
Детерминацийн коэф, R2

SSR
R 
2

SST
Энд

0  R 1
2

Детерминацийн коэф, R2

SSR регрессээр ттайлбарл гдах кв - н нийлбэр
R 
2

SST кв - н нийт нийлбэр

Нэг үл хамаарах хувьсагчтай тохиолдолд
детерминацийн коэф нь:

энд:
R r2 2

R2 = детерминацийн коэф
r = энгийн корреляцийн коэф

Жишээ

y
R2 = 1

x ба y-н төгс шугаман
хамаарал:
x
R2 = 1
y

x
R2 = +1

Жишээ

y
0 < R2 < 1

x ба y-н сул шугаман
хамаарал:
x
x-ээр y-н зарим хэсгийг
y
тайлбарлаж чадна.

x

Жишээ

R2 = 0
y
x ба y нь шугаман
хамааралгүй:

x-ээр y-г тайлбарлаж
R2 = 0
x чадахгүй.

Excel үр дүн
SSR 18934.9348
R 2
  0.58082
Multiple R 0.76211 SST 32600.5000
R Square 0.58082
Adjusted R Х-ээр У-н 58.08%-г
Square 0.52842 тайлбарлаж чадна
Standard Error 41.33032
Observations 10

ANOVA Significance
df SS MS F F
18934.934 11.084
Regression 1 18934.9348 8 8 0.01039

Residual 8 13665.5652 1708.1957
Total 9 32600.5000

Coefficien P- Upper
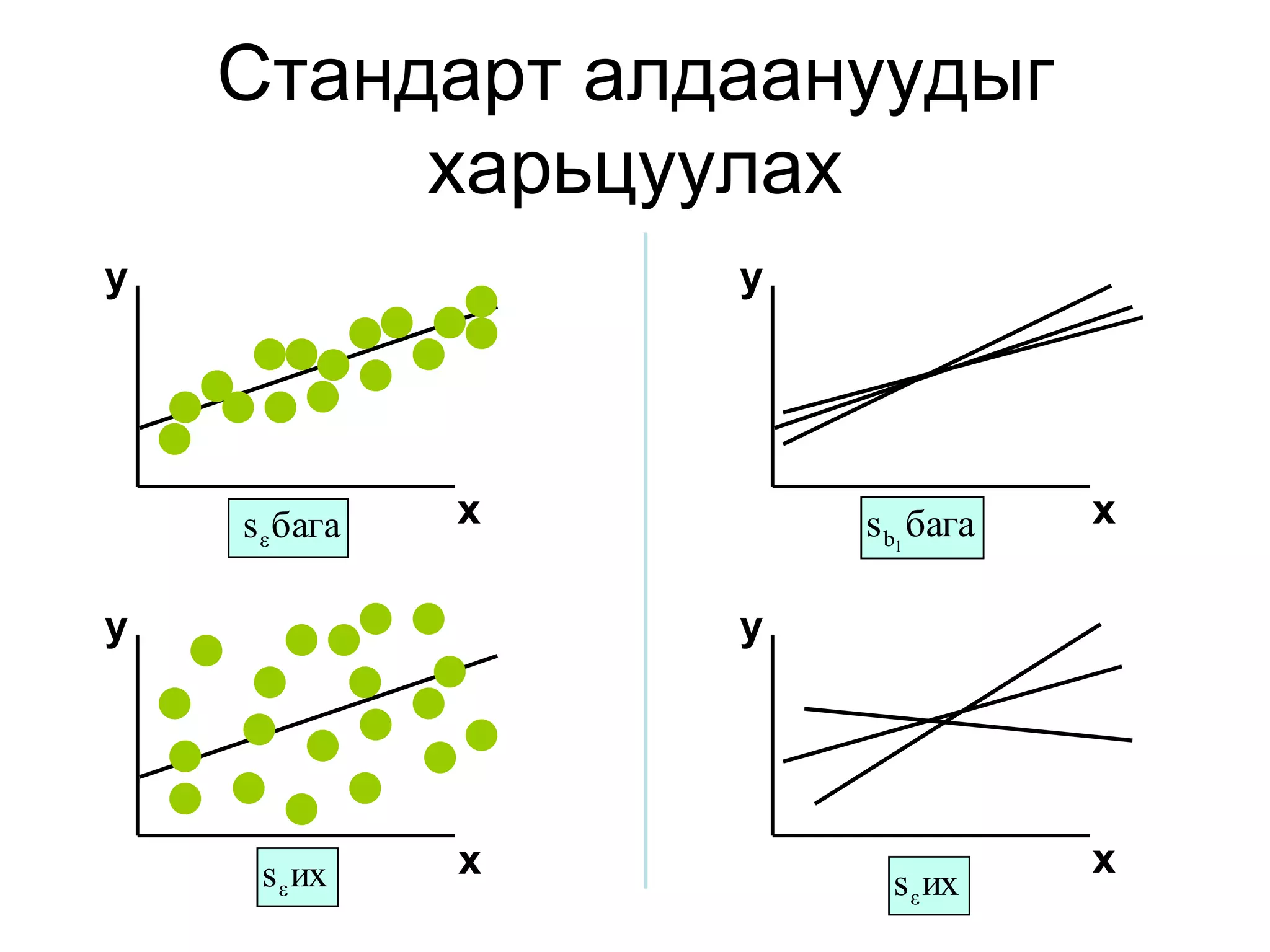
ts Standard Error t Stat value Lower 95% 95%

Стандарт алдаа

SSE
s 
n  k 1

SSE= алдааны кв-н нийлбэр
n= түүврийн хэмжээ
К= үл хамаарах хувьсагчдын тоо

Налалтын коэф-н хэлбэлзэл
• (b1)-н стандарт алдаа нь:
sε sε
sb1  
 (x  x) 2
(  x)
x  n 2
2

Энд:
sb1 = налалтын коэф-н стандарт алдаа
SSE
sε  = стандарт алдаа
n2

Excel үр дүн
Multiple R
R Square
0.76211
0.58082
sε  41.33032
Adjusted R
Square 0.52842
Standard Error
Observations
41.33032
10
sb1  0.03297
ANOVA Significance
df SS MS F F
18934.934 11.084
Regression 1 18934.9348 8 8 0.01039

Residual 8 13665.5652 1708.1957
Total 9 32600.5000
Coefficien P- Upper
ts Standard Error t Stat value Lower 95% 95%
0.1289 232.0738
Intercept 98.24833 58.03348 1.69296 2 -35.57720 6
0.0103
Square Feet 0.10977 0.03297 3.32938 9 0.03374 0.18580

Стандарт алдаануудыг
харьцуулах
y y

s ε бага x s b1 бага x

y y

s ε их x x
s ε их

Т тест, налалтын коэф
• Эх олонлогийн налалтыг коэф-н тухай
таамаглал шалгах
– x ба y нь шугаман хамааралтай эсэх?
• Таамаглал
– H0: β1 = 0 (шугаман хамааралгүй)
– H1: β1  0 (шугаман хамааралтай)
• Тестийн статистик Энд :

b1  β1 b1 = налалт

t – β1 = Эх олонлогийн налалт
sb1 d.f.  n  2 sb1 =стандарт алдаа

Т тест, налалтын коэф

Үнэлэгдсэн регрессийн загвар:
(y) (x)
y  98.25  0.1098(x)

245 1400
312 1600
279 1700
Загварын налалт нь 0.1098
308 1875 Y-т Х нөлөөлдөг эсэх?
199 1100
219 1550
405 2350
324 2450
319 1425
255 1700

Жишээ
Тестийн статистик: t = 3.329
b1 sb1 t
H0: β1 = 0 Үр дүн:
HA: β1  0 Coefficient
Standard
Error t Stat
P-
value

Intercept 98.24833 58.03348 1.6929 0.1289
d.f. = 10-2 = 8

Х 0.10977 0.03297 3.3293 0.0103
/2=.025 /2=.025

Шийдвэр: H0 няцаана
Няцаах H0 Няцаахгүй H0 Няцаах H
-tα/2
0
tα/2 0
Дүгнэлт: Y-т Х нөлөөлнө
-2.3060 2.3060 3.329

Итгэх интервал
Итгэх интервал:
b1  t /2sb1 d.f. = n - 2

Coefficient Standard Upper
s Error t Stat P-value Lower 95% 95%

Intercept 98.24833 58.03348 1.69296 0.12892 -35.57720 232.07386

Х 0.10977 0.03297 3.32938 0.01039 0.03374 0.18580

Налалтын 95%-н итгэх интервал нь (0.0337, 0.1858)

Алдааны анализ
• Зорилт
– Шугаман эсэх
– Тогтмол дисперстэй эсэх
– Хэвийн тархалттай
• График
– Алдаа ба х –ийн зураглал
– Алдааны гистограмыг дүрслэх

Алдааны анализ

y y

x x
алдаа

x алдаа x

Шугаман биш
 Шугаман

Тогтмол дисперс

y y

x x
алдаа

x алдаа x

Дисперс нь тогтмол
бус
Дисперс нь тогтмол

Excel үр дүн

Алдаа

Таамаглас
ан утга Y Алдаа
1 251.92316 -6.923162
2 273.87671 38.12329
3 284.85348 -5.853484
4 304.06284 3.937162
5 218.99284 -19.99284
6 268.38832 -49.38832
7 356.20251 48.79749
8 367.17929 -43.17929
9 254.6674 64.33264
10 284.85348 -29.85348

АНХААРАЛ ТАВЬСАНД
БАЯРЛАЛАА

Correlation, other correlation

More Related Content

What's hot

Similar to Correlation, other correlation

More from zorigoo.sph

Correlation, other correlation