CVPR2009 tutorial: Kernel Methods in Computer Vision: part I: Introduction to Kernel Methods, Selecting and Combining Kernels
- 1. Kernel Methods in Computer Vision Christoph Lampert Matthew Blaschko Max Planck Institute for MPI Tübingen and Biological Cybernetics, Tübingen University of Oxford June 20, 2009
- 2. Overview... 14:00 – 15:00 Introduction to Kernel Classifiers 15:20 – 15:50 Selecting and Combining Kernels 15:50 – 16:20 Other Kernel Methods 16:40 – 17:40 Learning with Structured Outputs Slides and Additional Material (soon) http://www.christoph-lampert.de also watch out for
- 3. Introduction to Kernel Classifiers
- 4. Linear Classification Separates these two sample sets. height width
- 5. Linear Classification Separates these two sample sets. height width Linear Classification
- 6. Linear Regression Find a function that interpolates data points. 1.2 1.0 0.8 0.6 0.4 0.2 0.0 0.0 0.2 0.4 0.6 0.8 1.0
- 7. Linear Regression Find a function that interpolates data points. 1.2 1.0 0.8 0.6 0.4 0.2 0.0 0.0 0.2 0.4 0.6 0.8 1.0 Least Squares Regression
- 8. Linear Dimensionality Reduction Reduce the dimensionality of a dataset while preserving its structure. 4 3 2 1 0 -1 -2 -3 -4 -3 -2 -1 0 1 2 3
- 9. Linear Dimensionality Reduction Reduce the dimensionality of a dataset while preserving its structure. 4 3 2 1 0 -1 -2 -3 -4 -3 -2 -1 0 1 2 3 Principal Component Analysis
- 10. Linear Techniques Three different elementary tasks: classification, regression, dimensionality reduction. In each case, linear techniques are very successful.
- 11. Linear Techniques Linear techniques... often work well, most natural functions are smooth, smooth function can be approximated, at least locally, by linear functions. are fast and easy to solve elementary maths, even closed form solutions typically involve only matrix operation are intuitive solution can be visualized geometrically, solution corresponds to common sense.
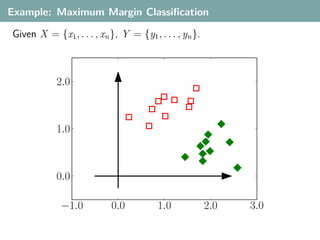
- 12. Example: Maximum Margin Classification Notation: data points X = {x1 , . . . , xn }, xi ∈ Rd , class labels Y = {y1 , . . . , yn }, yi ∈ {+1, −1}. linear (decision) function f : Rd → R, decide classes based on sign f : Rd → {−1, 1}. parameterize f (x) = a 1 x 1 + a 2 x 2 + . . . a n x n + a 0 ≡ w, x + b with w = (a 1 , . . . , a n ), b = a 0 . . , . is the scalar product is Rd . f is uniquely determined by w ∈ Rd and b ∈ R, but we usually ignore b and only study w b can be absorbed into w. Set w = (w, b), x = (x, 1).
- 13. Example: Maximum Margin Classification Given X = {x1 , . . . , xn }, Y = {y1 , . . . , yn }. 2.0 1.0 0.0 −1.0 0.0 1.0 2.0 3.0
- 14. Example: Maximum Margin Classification Given X = {x1 , . . . , xn }, Y = {y1 , . . . , yn }. Any w partitions the data space into two half-spaces, i.e. defines a classifier. 2.0 f (x) > 0 f (x) < 0 1.0 w 0.0 −1.0 0.0 1.0 2.0 3.0 “What’s the best w?”
- 15. Example: Maximum Margin Classification Given X = {x1 , . . . , xn }, Y = {y1 , . . . , yn }. What’s the best w? 2.0 2.0 1.0 1.0 0.0 0.0 −1.0 0.0 1.0 2.0 3.0 −1.0 0.0 1.0 2.0 3.0 Not these, since they misclassify many examples. Criterion 1: Enforce sign w, xi = yi for i = 1, . . . , n.
- 16. Example: Maximum Margin Classification Given X = {x1 , . . . , xn }, Y = {y1 , . . . , yn }. What’s the best w? 2.0 2.0 1.0 1.0 0.0 0.0 −1.0 0.0 1.0 2.0 3.0 −1.0 0.0 1.0 2.0 3.0 Better not these, since they would be “risky” for future samples. Criterion 2: Try to ensure sign w, x = y for future (x, y) as well.
- 17. Example: Maximum Margin Classification Given X = {x1 , . . . , xn }, Y = {y1 , . . . , yn }. Assume that future samples are similar to current ones. What’s the best w? 2.0 γ γ 1.0 0.0 −1.0 0.0 1.0 2.0 3.0 Maximize “stability”: use w such that we can maximally perturb the input samples without introducing misclassifications.
- 18. Example: Maximum Margin Classification Given X = {x1 , . . . , xn }, Y = {y1 , . . . , yn }. Assume that future samples are similar to current ones. What’s the best w? 2.0 2.0 n rgi ma ion γ γ γ reg 1.0 1.0 0.0 0.0 −1.0 0.0 1.0 2.0 3.0 −1.0 0.0 1.0 2.0 3.0 Maximize “stability”: use w such that we can maximally perturb the input samples without introducing misclassifications. Central quantity: w margin(x) = distance of x to decision hyperplane = w ,x
- 19. Example: Maximum Margin Classification Maximum-margin solution is determined by a maximization problem: max γ w∈Rd ,γ∈R+ subject to sign w, xi = yi for i = 1, . . . n. w , xi ≥γ for i = 1, . . . n. w Classify new samples using f (x) = w, x .
- 20. Example: Maximum Margin Classification Maximum-margin solution is determined by a maximization problem: max γ w∈Rd , w =1 γ∈R subject to yi w, xi ≥ γ for i = 1, . . . n. Classify new samples using f (x) = w, x .
- 21. Example: Maximum Margin Classification We can rewrite this as a minimization problem: 2 mind w w∈R subject to yi w, xi ≥ 1 for i = 1, . . . n. Classify new samples using f (x) = w, x .
- 22. Example: Maximum Margin Classification From the view of optimization theory 2 mind w w∈R subject to yi w, xi ≥ 1 for i = 1, . . . n is rather easy: The objective function is differentiable and convex. The constraints are all linear. We can find the globally optimal w in O(n 3 ) (or faster).
- 23. Linear Separability What is the best w for this dataset? height width
- 24. Linear Separability What is the best w for this dataset? height width Not this.
- 25. Linear Separability What is the best w for this dataset? height width Not this.
- 26. Linear Separability What is the best w for this dataset? height width Not this.
- 27. Linear Separability What is the best w for this dataset? height width Not this.
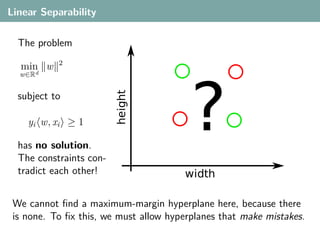
- 28. Linear Separability The problem 2 min w ? w∈Rd height subject to yi w, xi ≥ 1 has no solution. The constraints con- tradict each other! width We cannot find a maximum-margin hyperplane here, because there is none. To fix this, we must allow hyperplanes that make mistakes.
- 29. Linear Separability What is the best w for this dataset? height width
- 30. Linear Separability What is the best w for this dataset? n a tio ol vi in height a rg m ξ width Possibly this one, even though one sample is misclassified.
- 31. Linear Separability What is the best w for this dataset? height width
- 32. Linear Separability What is the best w for this dataset? small in marg ve r y height width Maybe not this one, even though all points are classified correctly.
- 33. Linear Separability What is the best w for this dataset? n tio height a ol vi in a rg m ξ width Trade-off: large margin vs. few mistakes on training set
- 34. Solving for Soft-Margin Solution Mathematically, we formulate the trade-off by slack-variables ξi : n 2 min w +C ξi w∈R ,ξi ∈R+ d i=1 subject to yi w, xi ≥ 1 − ξi for i = 1, . . . n. We can fulfill every constraint by choosing ξi large enough. The larger ξi , the larger the objective (that we try to minimize). C is a regularization/trade-off parameter: small C → constraints are easily ignored large C → constraints are hard to ignore C = ∞ → hard margin case → no training error Note: The problem is still convex and efficiently solvable.
- 35. Linear Separability So, what is the best soft-margin w for this dataset? y x None. We need something non-linear!
- 36. Non-Linear Classification: Stacking Idea 1) Use classifier output as input to other (linear) classifiers: fi=<wi,x> σ(f5(x')) σ(f1(x)) σ(f2(x)) σ(f3(x)) σ(f4(x)) Multilayer Perceptron (Artificial Neural Network) or Boosting ⇒ decisions depend non-linearly on x and wj .
- 37. Non-linearity: Data Preprocessing Idea 2) Preprocess the data: y This dataset is not (well) linearly separable: x θ This one is: r In fact, both are the same dataset! Top: Cartesian coordinates. Bottom: polar coordinates
- 38. Non-linearity: Data Preprocessing y Non-linear separation x θ Linear separation r Linear classifier in polar space; acts non-linearly in Cartesian space.
- 39. Generalized Linear Classifier Given X = {x1 , . . . , xn }, Y = {y1 , . . . , yn }. Given any (non-linear) feature map ϕ : Rk → Rm . Solve the minimization for ϕ(x1 ), . . . , ϕ(xn ) instead of x1 , . . . , xn : n 2 min w +C ξi w∈R ,ξi ∈R+ m i=1 subject to yi w, ϕ(xi ) ≥ 1 − ξi for i = 1, . . . n. The weight vector w now comes from the target space Rm . Distances/angles are measure by the scalar product . , . in Rm . Classifier f (x) = w, ϕ(x) is linear in w, but non-linear in x.
- 40. Example Feature Mappings Polar coordinates: √ x x 2 + y2 ϕ: → y ∠(x, y) d-th degree polynomials: 2 2 d d ϕ : x1 , . . . , xn → 1, x1 , . . . , xn , x1 , . . . , xn , . . . , x1 , . . . , xn Distance map: ϕ:x→ x − pi , . . . , x − pN for a set of N prototype vectors pi , i = 1, . . . , N .
- 41. Is this enough? In this example, changing the coordinates did help. Does this trick always work? y θ x r ↔
- 42. Is this enough? In this example, changing the coordinates did help. Does this trick always work? y θ x r ↔ Answer: In a way, yes! Lemma Let (xi )i=1,...,n with xi = xj for i = j. Let ϕ : Rk → Rm be a feature map. If the set ϕ(xi )i=1,...,n is linearly independent, then the points ϕ(xi )i=1,...,n are linearly separable. Lemma If we choose m > n large enough, we can always find a map ϕ.
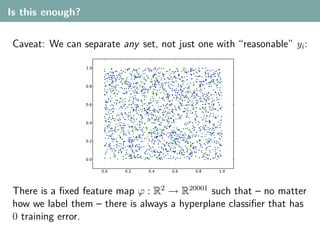
- 43. Is this enough? Caveat: We can separate any set, not just one with “reasonable” yi : There is a fixed feature map ϕ : R2 → R20001 such that – no matter how we label them – there is always a hyperplane classifier that has zero training error.
- 44. Is this enough? Caveat: We can separate any set, not just one with “reasonable” yi : There is a fixed feature map ϕ : R2 → R20001 such that – no matter how we label them – there is always a hyperplane classifier that has 0 training error.
- 45. Representer Theorem Solve the soft-margin minimization for ϕ(x1 ), . . . , ϕ(xn ) ∈ Rm : n 2 min w +C ξi (1) w∈Rm ,ξi ∈R+ i=1 subject to yi w, ϕ(xi ) ≥ 1 − ξi for i = 1, . . . n. For large m, won’t solving for w ∈ Rm become impossible?
- 46. Representer Theorem Solve the soft-margin minimization for ϕ(x1 ), . . . , ϕ(xn ) ∈ Rm : n 2 min w +C ξi (1) w∈Rm ,ξi ∈R+ i=1 subject to yi w, ϕ(xi ) ≥ 1 − ξi for i = 1, . . . n. For large m, won’t solving for w ∈ Rm become impossible? No! Theorem (Representer Theorem) The minimizing solution w to problem (1) can always be written as n w= αj ϕ(xj ) for coefficients α1 , . . . , αn ∈ R. j=1
- 47. Kernel Trick The representer theorem allows us to rewrite the optimization: n 2 min w +C ξi w∈R ,ξi ∈R+ m i=1 subject to yi w, ϕ(xi ) ≥ 1 − ξi for i = 1, . . . n. n Insert w = j=1 αj ϕ(xj ):
- 48. Kernel Trick We can minimize over αi instead of w: n n 2 min αj ϕ(xj ) +C ξi αi ∈R,ξi ∈R+ j=1 i=1 subject to n yi αj ϕ(xj ), ϕ(xi ) ≥ 1 − ξi for i = 1, . . . n. j=1
- 49. Kernel Trick 2 Use w = w, w : n n min αj αk ϕ(xj ), ϕ(xk ) + C ξi αi ∈R,ξi ∈R+ j,k=1 i=1 subject to n yi αj ϕ(xj ), ϕ(xi ) ≥ 1 − ξi for i = 1, . . . n. j=1 Note: ϕ only occurs in ϕ(.), ϕ(.) pairs.
- 50. Kernel Trick Set ϕ(x), ϕ(x ) =: k(x, x ), called kernel function. n n min αj αk k(xj , xk ) + C ξi αi ∈R,ξi ∈R+ j,k=1 i=1 subject to n yi αj k(xj , xi ) ≥ 1 − ξi for i = 1, . . . n. j=1 The maximum-margin classifier in this form with a kernel function is often called Support-Vector Machine (SVM).
- 51. Why use k(x, x ) instead of ϕ(x), ϕ(x ) ? 1) Speed: We might find an expression for k(xi , xj ) that is faster to calculate than forming ϕ(xi ) and then ϕ(xi ), ϕ(xj ) . Example: 2nd-order polynomial kernel (here for x ∈ R1 ): √ ϕ : x → (1, 2x, x 2 ) ∈ R3 √ √ ϕ(xi ), ϕ(xj ) = (1, 2xi , xi2 ), (1, 2xj , xj2 ) = 1 + 2xi xj + xi2 xj2 But equivalently (and faster) we can calculate without ϕ: k(xi , xj ) : = (1 + xi xj )2 = 1 + 2xi xj + xi2 xj2
- 52. Why use k(x, x ) instead of ϕ(x), ϕ(x ) ? 2) Flexibility: There are kernel functions k(xi , xj ), for which we know that a feature transformation ϕ exists, but we don’t know what ϕ is.
- 53. Why use k(x, x ) instead of ϕ(x), ϕ(x ) ? 2) Flexibility: There are kernel functions k(xi , xj ), for which we know that a feature transformation ϕ exists, but we don’t know what ϕ is. How that??? Theorem Let k : X × X → R be a positive definite kernel function. Then there exists a Hilbert Space H and a mapping ϕ : X → H such that k(x, x ) = ϕ(x), ϕ(x ) H where . , . H is the inner product in H.
- 54. Positive Definite Kernel Function Definition (Positive Definite Kernel Function) Let X be a non-empty set. A function k : X × X → R is called positive definite kernel function, iff k is symmetric, i.e. k(x, x ) = k(x , x) for all x, x ∈ X . For any set of points x1 , . . . , xn ∈ X , the matrix Kij = (k(xi , xj ))i,j is positive (semi-)definite, i.e. for all vectors t ∈ Rn : n ti Kij tj ≥ 0. i,j=1 Note: Instead of “positive definite kernel function”, we will often just say “kernel”.
- 55. Hilbert Spaces Definition (Hilbert Space) A Hilbert Space H is a vector space H with an inner product . , . H , e.g. a mapping .,. H : H × H → R which is symmetric: v, v H = v , v H for all v, v ∈ H , positive definite: v, v H ≥ 0 for all v ∈ H , where v, v H = 0 only for v = 0 ∈ H . bilinear: av, v H = a v, v H for v ∈ H , a ∈ R v + v , v H = v, v H + v , v H We can treat a Hilbert space like some Rn , if we only use concepts like vectors, angles, distances. Note: dim H = ∞ is possible!
- 56. Kernels for Arbitrary Sets Theorem Let k : X × X → R be a positive definite kernel function. Then there exists a Hilbert Space H and a mapping ϕ : X → H such that k(x, x ) = ϕ(x), ϕ(x ) H where . , . H is the inner product in H. Translation Take any set X and any function k : X × X → R. If k is a positive definite kernel, then we can use k to learn a (soft) maximum-margin classifier for the elements in X ! Note: X can be any set, e.g. X = { all images }.
- 57. How to Check if a Function is a Kernel Problem: Checking if a given k : X × X → R fulfills the conditions for a kernel is difficult: We need to prove or disprove n ti k(xi , xj )tj ≥ 0. i,j=1 for any set x1 , . . . , xn ∈ X and any t ∈ Rn for any n ∈ N. Workaround: It is easy to construct functions k that are positive definite kernels.
- 58. Constructing Kernels 1) We can construct kernels from scratch: For any ϕ : X → Rm , k(x, x ) = ϕ(x), ϕ(x ) Rm is a kernel. If d : X × X → R is a distance function, i.e. • d(x, x ) ≥ 0 for all x, x ∈ X , • d(x, x ) = 0 only for x = x , • d(x, x ) = d(x , x) for all x, x ∈ X , • d(x, x ) ≤ d(x, x ) + d(x , x ) for all x, x , x ∈ X , then k(x, x ) := exp(−d(x, x )) is a kernel.
- 59. Constructing Kernels 1) We can construct kernels from scratch: For any ϕ : X → Rm , k(x, x ) = ϕ(x), ϕ(x ) Rm is a kernel. If d : X × X → R is a distance function, i.e. • d(x, x ) ≥ 0 for all x, x ∈ X , • d(x, x ) = 0 only for x = x , • d(x, x ) = d(x , x) for all x, x ∈ X , • d(x, x ) ≤ d(x, x ) + d(x , x ) for all x, x , x ∈ X , then k(x, x ) := exp(−d(x, x )) is a kernel. 2) We can construct kernels from other kernels: if k is a kernel and α > 0, then αk and k + α are kernels. if k1 , k2 are kernels, then k1 + k2 and k1 · k2 are kernels.
- 60. Constructing Kernels Examples for kernels for X = Rd : any linear combination j αj kj with αj ≥ 0, polynomial kernels k(x, x ) = (1 + x, x )m , m > 0 x−x 2 Gaussian or RBF k(x, x ) = exp − 2σ 2 with σ > 0,
- 61. Constructing Kernels Examples for kernels for X = Rd : any linear combination j αj kj with αj ≥ 0, polynomial kernels k(x, x ) = (1 + x, x )m , m > 0 x−x 2 Gaussian or RBF k(x, x ) = exp − 2σ 2 with σ > 0, Examples for kernels for other X : k(h, h ) = n min(hi , hi ) for n-bin histograms h, h . i=1 k(p, p ) = exp(−KL(p, p )) with KL the symmetrized KL-divergence between positive probability distributions. k(s, s ) = exp(−D(s, s )) for strings s, s and D = edit distance
- 62. Constructing Kernels Examples for kernels for X = Rd : any linear combination j αj kj with αj ≥ 0, polynomial kernels k(x, x ) = (1 + x, x )m , m > 0 x−x 2 Gaussian or RBF k(x, x ) = exp − 2σ 2 with σ > 0, Examples for kernels for other X : k(h, h ) = n min(hi , hi ) for n-bin histograms h, h . i=1 k(p, p ) = exp(−KL(p, p )) with KL the symmetrized KL-divergence between positive probability distributions. k(s, s ) = exp(−D(s, s )) for strings s, s and D = edit distance Examples for functions X × X → R that are not kernels: tanh (κ x, x + θ) (matrix Kij can have negative eigenvalues)
- 63. Kernels in Computer Vision X = { images }, treat feature extraction as part of kernel definition OCR/handwriting recognition resize image, normalize brightness/contrast/rotation/skew polynomial kernel k(x, x ) = (1 + x, x )d , d > 0 [DeCoste, Schölkopf. ML2002] Pedestrian detection resize image, calculate local intensity gradient directions local thresholding + linear kernel [Dalal, Triggs. CVPR 2005] or local L1 -normalization + histogram intersection kernel [Maji, Berg, Malik. CVPR 2008]
- 64. Kernels in Computer Vision X = { images }, treat feature extraction as part of kernel definition object category recognition extract local image descriptors, e.g. SIFT calculate multi-level pyramid histograms h l,k (x) pyramid match kernel [Grauman, Darrell. ICCV 2005] L 2l−1 l kPMK (x, x ) = 2 min h l,k (x), h l,k (x ) l=1 k=1 scene/object category recognition extract local image descriptors, e.g. SIFT quantize descriptors into bag-of-words histograms χ2 -kernel [Puzicha, Buhmann, Rubner, Tomasi. ICCV1999] kχ2 (h, h ) = exp −γχ2 (h, h ) for γ > 0 K (hk − hk )2 χ2 (h, h ) = k=1 hk + hk
- 65. Summary Linear methods are popular and well understood classification, regression, dimensionality reduction, ... Kernels are at the same time... 1) Similarity measure between (arbitrary) objects, 2) Scalar products in a (hidden) vector space. Kernelization can make linear techniques more powerful implicit preprocessing, non-linear in the original data. still linear in some feature space ⇒ still intuitive/interpretable Kernels can be defined over arbitrary inputs, e.g. images unified framework for all preprocessing steps different features, normalization, etc., becomes kernel choices
- 66. What did we not see? We have skipped the largest part of theory on kernel methods: Optimization Dualization Algorithms to train SVMs Kernel Design Systematic methods to construct data-dependent kernels. Statistical Interpretations What do we assume about samples? What performance can we expect? Generalization Bounds The test error of a (kernelized) linear classifier can be controlled using its modelling error and its training error. “Support Vectors” This and much more in standard references.
- 67. Selecting and Combining Kernels
- 68. Selecting From Multiple Kernels Typically, one has many different kernels to choose from: different functional forms linear, polynomial, RBF, . . . different parameters polynomial degree, Gaussian bandwidth, . . .
- 69. Selecting From Multiple Kernels Typically, one has many different kernels to choose from: different functional forms linear, polynomial, RBF, . . . different parameters polynomial degree, Gaussian bandwidth, . . . Different image features give rise to different kernels Color histograms, SIFT bag-of-words, HOG, Pyramid match, Spatial pyramids, . . .
- 70. Selecting From Multiple Kernels Typically, one has many different kernels to choose from: different functional forms linear, polynomial, RBF, . . . different parameters polynomial degree, Gaussian bandwidth, . . . Different image features give rise to different kernels Color histograms, SIFT bag-of-words, HOG, Pyramid match, Spatial pyramids, . . . How to choose? Ideally, based on the kernels’ performance on task at hand: estimate by cross-validation or validation set error Classically part of “Model Selection”.
- 71. Kernel Parameter Selection Note: Model Selection makes a difference! Action Classification, KTH dataset Method Accuracy Dollár et al. VS-PETS 2005: ”SVM classifier“ 80.66 Nowozin et al., ICCV 2007: ”baseline RBF“ 85.19 identical features, same kernel function difference: Nowozin used cross-validation for model selection (bandwidth and C ) Note: there is no overfitting involved here. Model selection is fully automatic and uses only training data.
- 72. Kernel Parameter Selection Rule of thumb for kernel parameters For kernels based on the exponential function 1 k(x, x ) = exp(− X (x, x )) γ with any X , set γ ≈ meani,j=1,...,n X (xi , xj ). Sometimes better: use only X (xi , xj ) with yi = yj . In general, if there are several classes, then the kernel matrix : Kij = k(xi , xj ) should have a block structure w.r.t. the classes.
- 73. 1.0 1.0 0 0.9 0 0 0.9 2.4 1.0 y 0.8 0.8 10 10 1.6 10 0.7 0.7 0.5 x 20 0.6 20 0.8 20 0.6 0.5 0.5 0.0 0.0 30 0.4 30 30 0.4 −0.8 −0.5 0.3 0.3 40 0.2 40 −1.6 40 0.2 −1.0 0.1 −2.4 0.1 −2.0 −1.0 0.0 1.0 2.0 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0 10 20 30 40 50 0.0 two moons label “kernel” linear RBF: γ = 0.001 1.0 1.0 1.0 1.0 0 0.9 0 0.9 0 0.9 0 0.9 0.8 0.8 0.8 0.8 10 10 10 10 0.7 0.7 0.7 0.7 20 0.6 20 0.6 20 0.6 20 0.6 0.5 0.5 0.5 0.5 30 0.4 30 0.4 30 0.4 30 0.4 0.3 0.3 0.3 0.3 40 0.2 40 0.2 40 0.2 40 0.2 0.1 0.1 0.1 0.1 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0.0 γ = 0.01 γ = 0.1 γ=1 γ = 10 1.0 1.0 0 0.9 0 0.9 0.8 0.8 10 10 0.7 0.7 20 0.6 20 0.6 0.5 0.5 30 0.4 30 0.4 0.3 0.3 40 0.2 40 0.2 0.1 0.1 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0.0 γ = 100 γ = 1000
- 74. 1.0 1.0 0 0.9 0 0 0.9 2.4 1.0 y 0.8 0.8 10 10 1.6 10 0.7 0.7 0.5 x 20 0.6 20 0.8 20 0.6 0.5 0.5 0.0 0.0 30 0.4 30 30 0.4 −0.8 −0.5 0.3 0.3 40 0.2 40 −1.6 40 0.2 −1.0 0.1 −2.4 0.1 −2.0 −1.0 0.0 1.0 2.0 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0 10 20 30 40 50 0.0 two moons label “kernel” linear RBF: γ = 0.001 1.0 1.0 1.0 1.0 0 0.9 0 0.9 0 0.9 0 0.9 0.8 0.8 0.8 0.8 10 10 10 10 0.7 0.7 0.7 0.7 20 0.6 20 0.6 20 0.6 20 0.6 0.5 0.5 0.5 0.5 30 0.4 30 0.4 30 0.4 30 0.4 0.3 0.3 0.3 0.3 40 0.2 40 0.2 40 0.2 40 0.2 0.1 0.1 0.1 0.1 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0.0 γ = 0.01 γ = 0.1 γ=1 γ = 10 1.0 1.0 1.0 0 0.9 0 0.9 0 0.9 0.8 0.8 0.8 10 10 10 0.7 0.7 0.7 20 0.6 20 0.6 20 0.6 0.5 0.5 0.5 30 0.4 30 0.4 30 0.4 0.3 0.3 0.3 40 0.2 40 0.2 40 0.2 0.1 0.1 0.1 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0.0 γ = 100 γ = 1000 γ = 0.6 rule of thumb
- 75. 1.0 1.0 0 0.9 0 0 0.9 2.4 1.0 y 0.8 0.8 10 10 1.6 10 0.7 0.7 0.5 x 20 0.6 20 0.8 20 0.6 0.5 0.5 0.0 0.0 30 0.4 30 30 0.4 −0.8 −0.5 0.3 0.3 40 0.2 40 −1.6 40 0.2 −1.0 0.1 −2.4 0.1 −2.0 −1.0 0.0 1.0 2.0 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0 10 20 30 40 50 0.0 two moons label “kernel” linear RBF: γ = 0.001 1.0 1.0 1.0 1.0 0 0.9 0 0.9 0 0.9 0 0.9 0.8 0.8 0.8 0.8 10 10 10 10 0.7 0.7 0.7 0.7 20 0.6 20 0.6 20 0.6 20 0.6 0.5 0.5 0.5 0.5 30 0.4 30 0.4 30 0.4 30 0.4 0.3 0.3 0.3 0.3 40 0.2 40 0.2 40 0.2 40 0.2 0.1 0.1 0.1 0.1 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0.0 γ = 0.01 γ = 0.1 γ=1 γ = 10 1.0 1.0 1.0 1.0 0 0.9 0 0.9 0 0.9 0 0.9 0.8 0.8 0.8 0.8 10 10 10 10 0.7 0.7 0.7 0.7 20 0.6 20 0.6 20 0.6 20 0.6 0.5 0.5 0.5 0.5 30 0.4 30 0.4 30 0.4 30 0.4 0.3 0.3 0.3 0.3 40 0.2 40 0.2 40 0.2 40 0.2 0.1 0.1 0.1 0.1 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0.0 0 10 20 30 40 50 0.0 γ = 100 γ = 1000 γ = 0.6 γ = 1.6 rule of thumb 5-fold CV
- 76. Kernel Selection ↔ Kernel Combination Is there a single best kernel at all? Kernels are typcally designed to capture one aspect of the data texture, color, edges, . . . Choosing one kernel means to select exactly one such aspect.
- 77. Kernel Selection ↔ Kernel Combination Is there a single best kernel at all? Kernels are typcally designed to capture one aspect of the data texture, color, edges, . . . Choosing one kernel means to select exactly one such aspect. Combining aspects if often better than Selecting. Method Accuracy Colour 60.9 ± 2.1 Shape 70.2 ± 1.3 Texture 63.7 ± 2.7 HOG 58.5 ± 4.5 HSV 61.3 ± 0.7 siftint 70.6 ± 1.6 siftbdy 59.4 ± 3.3 combination 85.2 ± 1.5 Mean accuracy on Oxford Flowers dataset [Gehler, Nowozin: ICCV2009]
- 78. Combining Two Kernels For two kernels k1 , k2 : product k = k1 k2 is again a kernel Problem: very small kernel values suppress large ones average k = 1 (k1 + k2 ) is again a kernel 2 Problem: k1 , k2 on different scales. Re-scale first? convex combination kβ = (1 − β)k1 + βk2 with β ∈ [0, 1] Model selection: cross-validate over β ∈ {0, 0.1, . . . , 1}.
- 79. Combining Many Kernels Multiple kernels: k1 ,. . . ,kK all convex combinations are kernels: K K k= βj kj with βj ≥ 0, β = 1. j=1 j=1 Kernels can be “deactivated” by βj = 0. Combinatorial explosion forbids cross-validation over all combinations of βj Proxy: instead of CV, maximize SVM-objective. Each combined kernel induces a feature space. In which of the feature spaces can we best explain the training data, and achieve a large margin between the classes?
- 80. Feature Space View of Kernel Combination Each kernel kj induces a Hilbert Space Hj and a mapping ϕj : X → Hj . β The weighted kernel kj j := βj kj induces the same Hilbert Space Hj , but β a rescaled feature mapping ϕj j (x) := βj ϕj (x). β β k βj (x, x ) ≡ ϕj j (x), ϕj j (x ) H = βj ϕj (x), βj ϕj (x ) H = βj ϕj (x), ϕj (x ) H = βj k(x, x ). ˆ The linear combination k := K βj kj induces j=1 the product space H := ⊕K Hj , and j=1 the product mapping ϕ(x) := (ϕβ1 (x), . . . , ϕβn (x))t ˆ 1 n K K ˆ β β k(x, x ) ≡ ϕ(x), ϕ(x ) ˆ ˆ H = ϕj j (x), ϕj j (x ) H = βj k(x, x ) j=1 j=1
- 81. Feature Space View of Kernel Combination Implicit representation of a dataset using two kernels: Kernel k1 , feature representation ϕ1 (x1 ), . . . , ϕ1 (xn ) ∈ H1 Kernel k2 , feature representation ϕ2 (x1 ), . . . , ϕ2 (xn ) ∈ H2 Kernel Selection would most likely pick k2 . For k = (1 − β)k1 + βk2 , top is β = 0, bottom is β = 1.
- 82. Feature Space View of Kernel Combination β = 0.00 margin = 0.0000 5 √ 1.00φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.00φ1 (xi ) −1 −1 0 1 2 3 4 5
- 83. Feature Space View of Kernel Combination β = 1.00 margin = 0.1000 5 √ 0.00φ2 (xi ) H1 × H2 4 3 2 1 0 √ 1.00φ1 (xi ) −1 −1 0 1 2 3 4 5
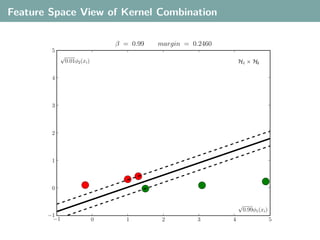
- 84. Feature Space View of Kernel Combination β = 0.99 margin = 0.2460 5 √ 0.01φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.99φ1 (xi ) −1 −1 0 1 2 3 4 5
- 85. Feature Space View of Kernel Combination β = 0.98 margin = 0.3278 5 √ 0.02φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.98φ1 (xi ) −1 −1 0 1 2 3 4 5
- 86. Feature Space View of Kernel Combination β = 0.97 margin = 0.3809 5 √ 0.03φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.97φ1 (xi ) −1 −1 0 1 2 3 4 5
- 87. Feature Space View of Kernel Combination β = 0.95 margin = 0.4515 5 √ 0.05φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.95φ1 (xi ) −1 −1 0 1 2 3 4 5
- 88. Feature Space View of Kernel Combination β = 0.90 margin = 0.5839 5 √ 0.10φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.90φ1 (xi ) −1 −1 0 1 2 3 4 5
- 89. Feature Space View of Kernel Combination β = 0.80 margin = 0.7194 5 √ 0.20φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.80φ1 (xi ) −1 −1 0 1 2 3 4 5
- 90. Feature Space View of Kernel Combination β = 0.70 margin = 0.7699 5 √ 0.30φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.70φ1 (xi ) −1 −1 0 1 2 3 4 5
- 91. Feature Space View of Kernel Combination β = 0.65 margin = 0.7770 5 √ 0.35φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.65φ1 (xi ) −1 −1 0 1 2 3 4 5
- 92. Feature Space View of Kernel Combination β = 0.60 margin = 0.7751 5 √ 0.40φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.60φ1 (xi ) −1 −1 0 1 2 3 4 5
- 93. Feature Space View of Kernel Combination β = 0.50 margin = 0.7566 5 √ 0.50φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.50φ1 (xi ) −1 −1 0 1 2 3 4 5
- 94. Feature Space View of Kernel Combination β = 0.40 margin = 0.7365 5 √ 0.60φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.40φ1 (xi ) −1 −1 0 1 2 3 4 5
- 95. Feature Space View of Kernel Combination β = 0.30 margin = 0.7073 5 √ 0.70φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.30φ1 (xi ) −1 −1 0 1 2 3 4 5
- 96. Feature Space View of Kernel Combination β = 0.20 margin = 0.6363 5 √ 0.80φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.20φ1 (xi ) −1 −1 0 1 2 3 4 5
- 97. Feature Space View of Kernel Combination β = 0.10 margin = 0.4928 5 √ 0.90φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.10φ1 (xi ) −1 −1 0 1 2 3 4 5
- 98. Feature Space View of Kernel Combination β = 0.03 margin = 0.2870 5 √ 0.97φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.03φ1 (xi ) −1 −1 0 1 2 3 4 5
- 99. Feature Space View of Kernel Combination β = 0.02 margin = 0.2363 5 √ 0.98φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.02φ1 (xi ) −1 −1 0 1 2 3 4 5
- 100. Feature Space View of Kernel Combination β = 0.01 margin = 0.1686 5 √ 0.99φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.01φ1 (xi ) −1 −1 0 1 2 3 4 5
- 101. Feature Space View of Kernel Combination β = 0.00 margin = 0.0000 5 √ 1.00φ2 (xi ) H1 × H2 4 3 2 1 0 √ 0.00φ1 (xi ) −1 −1 0 1 2 3 4 5
- 102. Multiple Kernel Learning Can we calculate coefficients βj that realize the largest margin? Analyze: how does the margin depend on βj ? Remember standard SVM (here without slack variables): 2 min w H w∈H subject to yi w, xi H ≥1 for i = 1, . . . n. H and ϕ were induced by kernel k. New samples are classified by f (x) = w, x H.
- 103. Multiple Kernel Learning Insert K k(x, x ) = βj kj (x, x ) (2) j=1 with Hilbert space H = ⊕j√ j , H √ feature map ϕ(x) = ( β1 ϕ1 (x), . . . , βK ϕK (x))t , weight vector w = (w1 , . . . , wK )t . such that 2 2 w H = wj Hj (3) j w, ϕ(xi ) H = βj wj , ϕj (xi ) Hj (4) j
- 104. Multiple Kernel Learning For fixed βj , the largest margin hyperplane is given by 2 min wj Hj wj ∈Hj j subject to yi βj wj , ϕj (xi ) Hj ≥1 for i = 1, . . . n. j 0 Renaming vj = βj wj (and defining 0 = 0): 1 2 min vj Hj vj ∈Hj j βj subject to yi vj , ϕj (xi ) Hj ≥1 for i = 1, . . . n. j
- 105. Multiple Kernel Learning Therefore, best hyperplane for variable βj is given by: 1 2 min vj Hj (5) vj ∈Hj j βj β =1 j j βj ≥0 subject to yi vj , ϕj (xi ) Hj ≥1 for i = 1, . . . n. (6) j This optimization problem is jointly-convex in vj and βj . There is a unique global minimum, and we can find it efficiently!
- 106. Multiple Kernel Learning Same for soft-margin with slack-variables: 1 2 min vj Hj +C ξi (7) vj ∈Hj j βj i β =1 j j βj ≥0 ξi ∈R+ subject to yi vj , ϕj (xi ) Hj ≥ 1 − ξi for i = 1, . . . n. (8) j This optimization problem is jointly-convex in vj and βj . There is a unique global minimum, and we can find it efficiently!
- 107. Software for Multiple Kernel Learning Existing toolboxes allow Multiple-Kernel SVM training: Shogun (C++ with bindings to Matlab, Python etc.) http://www.fml.tuebingen.mpg.de/raetsch/projects/shogun MPI IKL (Matlab with libSVM, CoinIPopt) http://www.kyb.mpg.de/bs/people/pgehler/ikl-webpage/index.html SimpleMKL (Matlab) http://asi.insa-rouen.fr/enseignants/˜arakotom/code/mklindex.html SKMsmo (Matlab) http://www.di.ens.fr/˜fbach/ (older and slower than the others) Typically, one only has to specify the set of candidate kernels and the regularization parameter C .
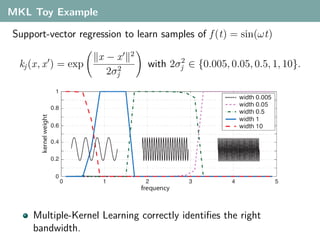
- 108. MKL Toy Example Support-vector regression to learn samples of f (t) = sin(ωt) 2 x −x 2 kj (x, x ) = exp 2 with 2σj ∈ {0.005, 0.05, 0.5, 1, 10}. 2σj Multiple-Kernel Learning correctly identifies the right bandwidth.
- 109. Combining Good Kernels Observation: if all kernels are reasonable, simple combination methods work as well as difficult ones (and are much faster): Single features Combination methods Method Accuracy Time Method Accuracy Time Colour 60.9 ± 2.1 3 product 85.5 ± 1.2 2 Shape 70.2 ± 1.3 4 averaging 84.9 ± 1.9 10 Texture 63.7 ± 2.7 3 CG-Boost 84.8 ± 2.2 1225 HOG 58.5 ± 4.5 4 MKL (SILP) 85.2 ± 1.5 97 HSV 61.3 ± 0.7 3 MKL (Simple) 85.2 ± 1.5 152 siftint 70.6 ± 1.6 4 LP-β 85.5 ± 3.0 80 siftbdy 59.4 ± 3.3 5 LP-B 85.4 ± 2.4 98 Mean accuracy and total runtime (model selection, training, testing) on Oxford Flowers dataset [Gehler, Nowozin: ICCV2009]
- 110. Combining Good and Bad kernels Observation: if some kernels are helpful, but others are not, smart techniques are better. Performance with added noise features 90 85 80 75 accuracy 70 65 product 60 average CG−Boost 55 MKL (silp or simple) 50 LP−β LP−B 45 01 5 10 25 50 no. noise features added Mean accuracy on Oxford Flowers dataset [Gehler, Nowozin: ICCV2009]
- 111. Example: Multi-Class Object Localization MKL for joint prediction of different object classes. Objects in images do not occur independently of each other. Chairs and tables often occur together in indoor scenes. Busses often occur together with cars in street scenes. Chairs rarely occur together with cars. One can make use of these dependencies to improve prediction.
- 112. Example: Multi-Class Object Localization Predict candidate regions for all object classes. Train a decision function for each class (red), taking into account candidate regions for all classes (red and green). Decide per-class which other object categories are worth using 20 2 2 k(I , I ) = β0 kχ (h, h ) + βj kχ (hj , hj ) j=1 h: feature histogram for the full image x hj : histogram for the region predicted for object class j in x Use MKL to learn weights βj , j = 0, . . . , 20. [Lampert and Blaschko, DAGM 2008]
- 113. Example: Multi-Class Object Localization Benchmark on PASCAL VOC 2006 and VOC 2007. Combination improves detection accuracy (black vs. blue).
- 114. Example: Multi-Class Object Localization Interpretation of Weights (VOC 2007): Every class decision 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 depends on the full image aeroplane [1] bicycle [2] and on the object box. bird [3] boat [4] bottle [5] bus [6] High image weights: car [7] cat [8] → scene classification? chair [9] cow [10] diningtable [11] dog [12] Intuitive connections: horse [13] motorbike [14] chair → diningtable, person [15] pottedplant [16] sheep [17] person → bottle, sofa [18] train [19] person → dog. tvmonitor [20] Many classes depend on rows: class to be detected the person class. columns: class candidate boxes
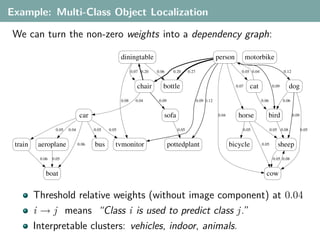
- 115. Example: Multi-Class Object Localization We can turn the non-zero weights into a dependency graph: diningtable person motorbike 0.07 0.20 0.06 0.20 0.27 0.05 0.04 0.12 chair bottle 0.07 cat 0.09 dog 0.08 0.04 0.09 0.09 0.12 0.06 0.06 car sofa 0.04 horse bird 0.09 0.05 0.04 0.05 0.05 0.05 0.05 0.05 0.08 0.05 train aeroplane 0.06 bus tvmonitor pottedplant bicycle 0.05 sheep 0.06 0.05 0.05 0.08 boat cow Threshold relative weights (without image component) at 0.04 i → j means “Class i is used to predict class j.” Interpretable clusters: vehicles, indoor, animals.
- 116. Summary Kernel Selection and Combination Model selection is important to achive highest accuracy Combining several kernels is often superior to selecting one Multiple-Kernel Learning Learn weights for the “best” linear kernel combination: unified approach to feature selection/combination. visit [Gehler, Nowozin. CVPR 2009] on Wednesday afternoon Beware: MKL is no silver bullet. Other and even simpler techniques might be superior! Always compare against single best, averaging, product. Warning: Caltech101/256 Be careful when reading kernel combination results Many results reported rely on “broken” Bosch kernel matrices



























































![Kernels in Computer Vision
X = { images }, treat feature extraction as part of kernel definition
OCR/handwriting recognition
resize image, normalize brightness/contrast/rotation/skew
polynomial kernel k(x, x ) = (1 + x, x )d , d > 0
[DeCoste, Schölkopf. ML2002]
Pedestrian detection
resize image, calculate local intensity gradient directions
local thresholding + linear kernel [Dalal, Triggs. CVPR 2005]
or
local L1 -normalization + histogram intersection kernel
[Maji, Berg, Malik. CVPR 2008]](https://image.slidesharecdn.com/statisticsandclusteringwithkernelsslide-lampertblaschko-biologicalcybernetics-2009-110407215618-phpapp01/85/CVPR2009-tutorial-Kernel-Methods-in-Computer-Vision-part-I-Introduction-to-Kernel-Methods-Selecting-and-Combining-Kernels-63-320.jpg)
![Kernels in Computer Vision
X = { images }, treat feature extraction as part of kernel definition
object category recognition
extract local image descriptors, e.g. SIFT
calculate multi-level pyramid histograms h l,k (x)
pyramid match kernel [Grauman, Darrell. ICCV 2005]
L 2l−1
l
kPMK (x, x ) = 2 min h l,k (x), h l,k (x )
l=1 k=1
scene/object category recognition
extract local image descriptors, e.g. SIFT
quantize descriptors into bag-of-words histograms
χ2 -kernel [Puzicha, Buhmann, Rubner, Tomasi. ICCV1999]
kχ2 (h, h ) = exp −γχ2 (h, h ) for γ > 0
K
(hk − hk )2
χ2 (h, h ) =
k=1 hk + hk](https://image.slidesharecdn.com/statisticsandclusteringwithkernelsslide-lampertblaschko-biologicalcybernetics-2009-110407215618-phpapp01/85/CVPR2009-tutorial-Kernel-Methods-in-Computer-Vision-part-I-Introduction-to-Kernel-Methods-Selecting-and-Combining-Kernels-64-320.jpg)












![Kernel Selection ↔ Kernel Combination
Is there a single best kernel at all?
Kernels are typcally designed to capture one aspect of the data
texture, color, edges, . . .
Choosing one kernel means to select exactly one such aspect.
Combining aspects if often better than Selecting.
Method Accuracy
Colour 60.9 ± 2.1
Shape 70.2 ± 1.3
Texture 63.7 ± 2.7
HOG 58.5 ± 4.5
HSV 61.3 ± 0.7
siftint 70.6 ± 1.6
siftbdy 59.4 ± 3.3
combination 85.2 ± 1.5
Mean accuracy on Oxford Flowers dataset [Gehler, Nowozin: ICCV2009]](https://image.slidesharecdn.com/statisticsandclusteringwithkernelsslide-lampertblaschko-biologicalcybernetics-2009-110407215618-phpapp01/85/CVPR2009-tutorial-Kernel-Methods-in-Computer-Vision-part-I-Introduction-to-Kernel-Methods-Selecting-and-Combining-Kernels-77-320.jpg)
![Combining Two Kernels
For two kernels k1 , k2 :
product k = k1 k2 is again a kernel
Problem: very small kernel values suppress large ones
average k = 1 (k1 + k2 ) is again a kernel
2
Problem: k1 , k2 on different scales. Re-scale first?
convex combination kβ = (1 − β)k1 + βk2 with β ∈ [0, 1]
Model selection: cross-validate over β ∈ {0, 0.1, . . . , 1}.](https://image.slidesharecdn.com/statisticsandclusteringwithkernelsslide-lampertblaschko-biologicalcybernetics-2009-110407215618-phpapp01/85/CVPR2009-tutorial-Kernel-Methods-in-Computer-Vision-part-I-Introduction-to-Kernel-Methods-Selecting-and-Combining-Kernels-78-320.jpg)




























![Combining Good Kernels
Observation: if all kernels are reasonable, simple combination
methods work as well as difficult ones (and are much faster):
Single features Combination methods
Method Accuracy Time Method Accuracy Time
Colour 60.9 ± 2.1 3 product 85.5 ± 1.2 2
Shape 70.2 ± 1.3 4 averaging 84.9 ± 1.9 10
Texture 63.7 ± 2.7 3 CG-Boost 84.8 ± 2.2 1225
HOG 58.5 ± 4.5 4 MKL (SILP) 85.2 ± 1.5 97
HSV 61.3 ± 0.7 3 MKL (Simple) 85.2 ± 1.5 152
siftint 70.6 ± 1.6 4 LP-β 85.5 ± 3.0 80
siftbdy 59.4 ± 3.3 5 LP-B 85.4 ± 2.4 98
Mean accuracy and total runtime (model selection, training, testing) on
Oxford Flowers dataset [Gehler, Nowozin: ICCV2009]](https://image.slidesharecdn.com/statisticsandclusteringwithkernelsslide-lampertblaschko-biologicalcybernetics-2009-110407215618-phpapp01/85/CVPR2009-tutorial-Kernel-Methods-in-Computer-Vision-part-I-Introduction-to-Kernel-Methods-Selecting-and-Combining-Kernels-109-320.jpg)
![Combining Good and Bad kernels
Observation: if some kernels are helpful, but others are not, smart
techniques are better.
Performance with added noise features
90
85
80
75
accuracy
70
65
product
60 average
CG−Boost
55 MKL (silp or simple)
50 LP−β
LP−B
45
01 5 10 25 50
no. noise features added
Mean accuracy on Oxford Flowers dataset [Gehler, Nowozin: ICCV2009]](https://image.slidesharecdn.com/statisticsandclusteringwithkernelsslide-lampertblaschko-biologicalcybernetics-2009-110407215618-phpapp01/85/CVPR2009-tutorial-Kernel-Methods-in-Computer-Vision-part-I-Introduction-to-Kernel-Methods-Selecting-and-Combining-Kernels-110-320.jpg)

![Example: Multi-Class Object Localization
Predict candidate regions for all object classes.
Train a decision function for each class (red), taking into
account candidate regions for all classes (red and green).
Decide per-class which other object
categories are worth using
20
2 2
k(I , I ) = β0 kχ (h, h ) + βj kχ (hj , hj )
j=1
h: feature histogram for the full image x
hj : histogram for the region predicted for object class j in x
Use MKL to learn weights βj , j = 0, . . . , 20.
[Lampert and Blaschko, DAGM 2008]](https://image.slidesharecdn.com/statisticsandclusteringwithkernelsslide-lampertblaschko-biologicalcybernetics-2009-110407215618-phpapp01/85/CVPR2009-tutorial-Kernel-Methods-in-Computer-Vision-part-I-Introduction-to-Kernel-Methods-Selecting-and-Combining-Kernels-112-320.jpg)

![Example: Multi-Class Object Localization
Interpretation of Weights (VOC 2007):
Every class decision
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
depends on the full image aeroplane [1]
bicycle [2]
and on the object box. bird [3]
boat [4]
bottle [5]
bus [6]
High image weights: car [7]
cat [8]
→ scene classification? chair [9]
cow [10]
diningtable [11]
dog [12]
Intuitive connections: horse [13]
motorbike [14]
chair → diningtable, person [15]
pottedplant [16]
sheep [17]
person → bottle, sofa [18]
train [19]
person → dog. tvmonitor [20]
Many classes depend on rows: class to be detected
the person class. columns: class candidate boxes](https://image.slidesharecdn.com/statisticsandclusteringwithkernelsslide-lampertblaschko-biologicalcybernetics-2009-110407215618-phpapp01/85/CVPR2009-tutorial-Kernel-Methods-in-Computer-Vision-part-I-Introduction-to-Kernel-Methods-Selecting-and-Combining-Kernels-114-320.jpg)
![Summary
Kernel Selection and Combination
Model selection is important to achive highest accuracy
Combining several kernels is often superior to selecting one
Multiple-Kernel Learning
Learn weights for the “best” linear kernel combination:
unified approach to feature selection/combination.
visit [Gehler, Nowozin. CVPR 2009] on Wednesday afternoon
Beware: MKL is no silver bullet.
Other and even simpler techniques might be superior!
Always compare against single best, averaging, product.
Warning: Caltech101/256
Be careful when reading kernel combination results
Many results reported rely on “broken” Bosch kernel matrices](https://image.slidesharecdn.com/statisticsandclusteringwithkernelsslide-lampertblaschko-biologicalcybernetics-2009-110407215618-phpapp01/85/CVPR2009-tutorial-Kernel-Methods-in-Computer-Vision-part-I-Introduction-to-Kernel-Methods-Selecting-and-Combining-Kernels-116-320.jpg)