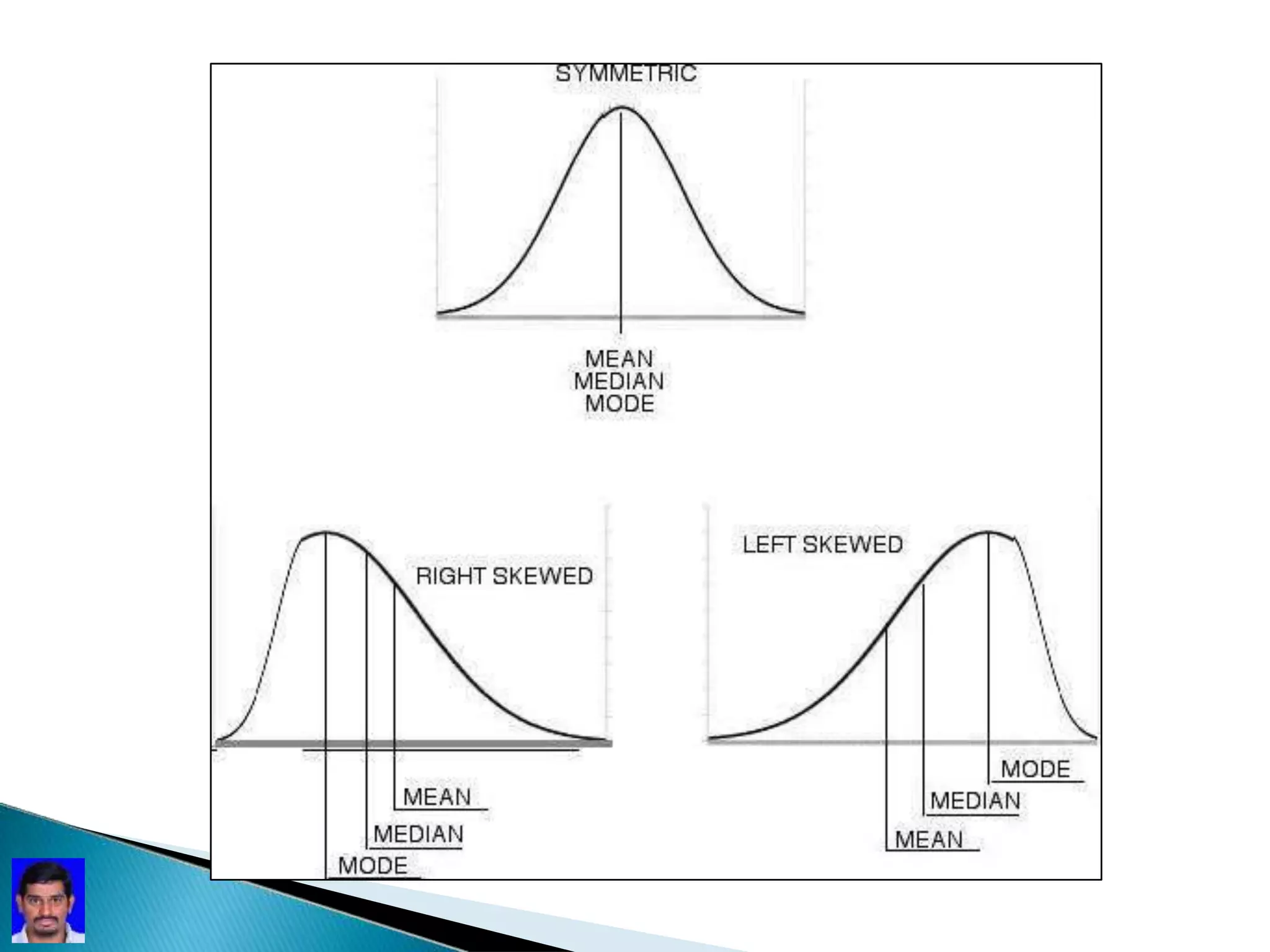
Descriptive statistics were used in ancient censuses by Babylonians and Egyptians to collect data on populations. Descriptive analysis involves collecting, organizing, summarizing, and presenting data using measures of central tendency like mean, median, and mode, and measures of variability like range, variance and standard deviation. These statistics describe and characterize samples to determine if they are normally distributed and can represent the larger population.