Gradient descent method
4 likes16,827 views
The document discusses gradient descent methods for unconstrained convex optimization problems. It introduces gradient descent as an iterative method to find the minimum of a differentiable function by taking steps proportional to the negative gradient. It describes the basic gradient descent update rule and discusses convergence conditions such as Lipschitz continuity, strong convexity, and condition number. It also covers techniques like exact line search, backtracking line search, coordinate descent, and steepest descent methods.
1 of 44
Downloaded 378 times





































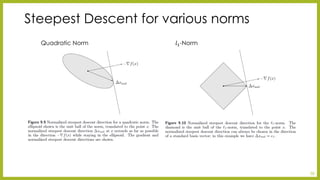

![Steepest Descent Convergence Rate
•Fact: Any norm can be bounded by ∙2, i.e., ∃훾, 훾∈(0,1] such that, 푥≥훾푥2푎푛푑푥∗≥훾푥2
•Theorem 5.5
•If f is strongly convex with respect to m and M, and ∙2has 훾, 훾as above then steepest decent with backtracking line search has linear convergence with rate
•푐=1−2푚훼 훾2min1, 훽훾 푀
•Proof: Will be proved in the lecture 6
40](https://image.slidesharecdn.com/131110gradientdescentmethod-141128132442-conversion-gate01/85/Gradient-descent-method-40-320.jpg)




Ad
Recommended
neural network



neural networkSTUDENT This document provides an introduction to neural networks, including their basic components and types. It discusses neurons, activation functions, different types of neural networks based on connection type, topology, and learning methods. It also covers applications of neural networks in areas like pattern recognition and control systems. Neural networks have advantages like the ability to learn from experience and handle incomplete information, but also disadvantages like the need for training and high processing times for large networks. In conclusion, neural networks can provide more human-like artificial intelligence by taking approximation and hard-coded reactions out of AI design, though they still require fine-tuning.
An overview of gradient descent optimization algorithms 



An overview of gradient descent optimization algorithms Hakky St This document provides an overview of various gradient descent optimization algorithms that are commonly used for training deep learning models. It begins with an introduction to gradient descent and its variants, including batch gradient descent, stochastic gradient descent (SGD), and mini-batch gradient descent. It then discusses challenges with these algorithms, such as choosing the learning rate. The document proceeds to explain popular optimization algorithms used to address these challenges, including momentum, Nesterov accelerated gradient, Adagrad, Adadelta, RMSprop, and Adam. It provides visualizations and intuitive explanations of how these algorithms work. Finally, it discusses strategies for parallelizing and optimizing SGD and concludes with a comparison of optimization algorithms.
Gradient descent method



Gradient descent methodProf. Neeta Awasthy This method gives the Artificial Neural Network, its much required tradeoff between cost function and processing powers
Naive Bayes



Naive BayesCloudxLab - Naive Bayes is a classification technique based on Bayes' theorem that uses "naive" independence assumptions. It is easy to build and can perform well even with large datasets.
- It works by calculating the posterior probability for each class given predictor values using the Bayes theorem and independence assumptions between predictors. The class with the highest posterior probability is predicted.
- It is commonly used for text classification, spam filtering, and sentiment analysis due to its fast performance and high success rates compared to other algorithms.
Neural networks.ppt



Neural networks.pptSrinivashR3 Neural networks are computational models inspired by the human brain. They consist of interconnected nodes that process information using a principle called neural learning. The document discusses the history and evolution of neural networks. It also provides examples of applications like image recognition, medical diagnosis, and predictive analytics. Neural networks are well-suited for problems that are difficult to solve with traditional algorithms like pattern recognition and classification.
TCP/IP Network ppt



TCP/IP Network pptextraganesh The document provides an overview of the TCP/IP model, describing each layer from application to network. The application layer allows programs access to networked services and contains high-level protocols like TCP and UDP. The transport layer handles reliable delivery via protocols like TCP and UDP. The internet layer organizes routing with the IP protocol. The network layer consists of device drivers and network interface cards that communicate with the physical transmission media.
Xgboost



XgboostVivian S. Zhang Our fall 12-Week Data Science bootcamp starts on Sept 21st,2015. Apply now to get a spot!
If you are hiring Data Scientists, call us at (1)888-752-7585 or reach [email protected] to share your openings and set up interviews with our excellent students.
---------------------------------------------------------------
Come join our meet-up and learn how easily you can use R for advanced Machine learning. In this meet-up, we will demonstrate how to understand and use Xgboost for Kaggle competition. Tong is in Canada and will do remote session with us through google hangout.
---------------------------------------------------------------
Speaker Bio:
Tong is a data scientist in Supstat Inc and also a master students of Data Mining. He has been an active R programmer and developer for 5 years. He is the author of the R package of XGBoost, one of the most popular and contest-winning tools on kaggle.com nowadays.
Pre-requisite(if any): R /Calculus
Preparation: A laptop with R installed. Windows users might need to have RTools installed as well.
Agenda:
Introduction of Xgboost
Real World Application
Model Specification
Parameter Introduction
Advanced Features
Kaggle Winning Solution
Event arrangement:
6:45pm Doors open. Come early to network, grab a beer and settle in.
7:00-9:00pm XgBoost Demo
Reference:
https://github.com/dmlc/xgboost
Optimization/Gradient Descent



Optimization/Gradient Descentkandelin The document discusses optimization and gradient descent algorithms. Optimization aims to select the best solution given some problem, like maximizing GPA by choosing study hours. Gradient descent is a method for finding the optimal parameters that minimize a cost function. It works by iteratively updating the parameters in the opposite direction of the gradient of the cost function, which points in the direction of greatest increase. The process repeats until convergence. Issues include potential local minimums and slow convergence.
Linear regression



Linear regressionMartinHogg9 A summary of what I learned about Linear Regression from the excellent Lazy Programmer Courses at https://lazyprogrammer.me
Decision tree



Decision treeR A Akerkar This document provides an overview of decision trees, including:
- Decision trees classify records by sorting them down the tree from root to leaf node, where each leaf represents a classification outcome.
- Trees are constructed top-down by selecting the most informative attribute to split on at each node, usually based on information gain.
- Trees can handle both numerical and categorical data and produce classification rules from paths in the tree.
- Examples of decision tree algorithms like ID3 that use information gain to select the best splitting attribute are described. The concepts of entropy and information gain are defined for selecting splits.
Linear regression with gradient descent



Linear regression with gradient descentSuraj Parmar Intro to the very popular optimization Technique(Gradient descent) with linear regression . Linear regression with Gradient descent on www.landofai.com
Concept learning and candidate elimination algorithm



Concept learning and candidate elimination algorithmswapnac12 This document discusses concept learning, which involves inferring a Boolean-valued function from training examples of its input and output. It describes a concept learning task where each hypothesis is a vector of six constraints specifying values for six attributes. The most general and most specific hypotheses are provided. It also discusses the FIND-S algorithm for finding a maximally specific hypothesis consistent with positive examples, and its limitations in dealing with noise or multiple consistent hypotheses. Finally, it introduces the candidate-elimination algorithm and version spaces as an improvement over FIND-S that can represent all consistent hypotheses.
Bayes Classification



Bayes Classificationsathish sak Uncertainty & Probability
Baye's rule
Choosing Hypotheses- Maximum a posteriori
Maximum Likelihood - Baye's concept learning
Maximum Likelihood of real valued function
Bayes optimal Classifier
Joint distributions
Naive Bayes Classifier
Feed forward ,back propagation,gradient descent



Feed forward ,back propagation,gradient descentMuhammad Rasel This document discusses gradient descent algorithms, feedforward neural networks, and backpropagation. It defines machine learning, artificial intelligence, and deep learning. It then explains gradient descent as an optimization technique used to minimize cost functions in deep learning models. It describes feedforward neural networks as having connections that move in one direction from input to output nodes. Backpropagation is mentioned as an algorithm for training neural networks.
Lecture 6: Ensemble Methods 



Lecture 6: Ensemble Methods Marina Santini What is an "ensemble learner"? How can we combine different base learners into an ensemble in order to improve the overall classification performance? In this lecture, we are providing some answers to these questions.
Inductive bias



Inductive biasswapnac12 This document discusses inductive bias in machine learning. It defines inductive bias as the assumptions that allow an inductive learning system to generalize beyond its training data. Without some biases, a learning system cannot rationally classify new examples. The document compares different learning algorithms based on the strength of their inductive biases, from weak biases like rote learning to stronger biases like preferring more specific hypotheses. It argues that all inductive learning systems require some inductive biases to generalize at all.
Decision Tree Learning



Decision Tree LearningMilind Gokhale This presentation was prepared as part of the curriculum studies for CSCI-659 Topics in Artificial Intelligence Course - Machine Learning in Computational Linguistics.
It was prepared under guidance of Prof. Sandra Kubler.
Machine Learning: Bias and Variance Trade-off



Machine Learning: Bias and Variance Trade-offInternational Institute of Information Technology (I²IT) Machine learning models involve a bias-variance tradeoff, where increased model complexity can lead to overfitting training data (high variance) or underfitting (high bias). Bias measures how far model predictions are from the correct values on average, while variance captures differences between predictions on different training data. The ideal model has low bias and low variance, accurately fitting training data while generalizing to new examples.
Support Vector Machine ppt presentation



Support Vector Machine ppt presentationAyanaRukasar Support vector machines (SVM) is a supervised machine learning algorithm used for both classification and regression problems. However, it is primarily used for classification. The goal of SVM is to create the best decision boundary, known as a hyperplane, that separates clusters of data points. It chooses extreme data points as support vectors to define the hyperplane. SVM is effective for problems that are not linearly separable by transforming them into higher dimensional spaces. It works well when there is a clear margin of separation between classes and is effective for high dimensional data. An example use case in Python is presented.
Support vector machine



Support vector machinezekeLabs Technologies Support vector machines are a type of supervised machine learning algorithm used for classification and regression analysis. They work by mapping data to high-dimensional feature spaces to find optimal linear separations between classes. Key advantages are effectiveness in high dimensions, memory efficiency using support vectors, and versatility through kernel functions. Hyperparameters like kernel type, gamma, and C must be tuned for best performance. Common kernels include linear, polynomial, and radial basis function kernels.
Linear Regression Algorithm | Linear Regression in Python | Machine Learning ...



Linear Regression Algorithm | Linear Regression in Python | Machine Learning ...Edureka! The document discusses linear regression algorithms. It begins with an introduction to regression analysis and its uses. Then it differentiates between linear and logistic regression. Next, it defines linear regression and discusses how to find the best fit regression line using the least squares method. It also explains how to check the goodness of fit using the R-squared method. Finally, it provides an overview of implementing linear regression using Python libraries.
Bias and variance trade off



Bias and variance trade offVARUN KUMAR This manuscript addresses the fundamentals of the trade-off relation between bias and variance in machine learning.
Activation function



Activation functionAstha Jain Artificial neural networks mimic the human brain by using interconnected layers of neurons that fire electrical signals between each other. Activation functions are important for neural networks to learn complex patterns by introducing non-linearity. Without activation functions, neural networks would be limited to linear regression. Common activation functions include sigmoid, tanh, ReLU, and LeakyReLU, with ReLU and LeakyReLU helping to address issues like vanishing gradients that can occur with sigmoid and tanh functions.
Lasso and ridge regression



Lasso and ridge regressionSreerajVA The document discusses different types of linear regression models including simple linear regression, multiple linear regression, ridge regression, lasso regression, and elastic net regression. It explains the concepts of slope, intercept, underfitting, overfitting, and regularization techniques used to constrain model weights. Specifically, it describes how ridge regression uses an L2 penalty, lasso regression uses an L1 penalty, and elastic net uses a combination of L1 and L2 penalties to regularize linear regression models and reduce overfitting.
Naïve Bayes Classifier Algorithm.pptx



Naïve Bayes Classifier Algorithm.pptxShubham Jaybhaye The document provides an overview of the Naive Bayes algorithm for classification problems. It begins by explaining that Naive Bayes is a supervised learning algorithm based on Bayes' theorem. It then explains the key aspects of Naive Bayes:
- It assumes independence between features (naive) and uses Bayes' theorem to calculate probabilities (Bayes).
- Bayes' theorem is used to calculate the probability of a hypothesis given observed data.
- An example demonstrates how Naive Bayes classifies weather data to predict whether to play or not play.
The document concludes by discussing the advantages, disadvantages, applications, and types of Naive Bayes models, as well as providing Python code to implement a Naive Bayes classifier.
Machine learning Lecture 2



Machine learning Lecture 2Srinivasan R The document summarizes key concepts in machine learning including concept learning as search, general-to-specific learning, version spaces, candidate elimination algorithm, and decision trees. It discusses how concept learning can be viewed as searching a hypothesis space to find the hypothesis that best fits the training examples. The candidate elimination algorithm represents the version space using the most general and specific hypotheses to efficiently learn from examples.
Instance Based Learning in Machine Learning



Instance Based Learning in Machine LearningPavithra Thippanaik Slides were formed by referring to the text Machine Learning by Tom M Mitchelle (Mc Graw Hill, Indian Edition) and by referring to Video tutorials on NPTEL
CS571: Gradient Descent



CS571: Gradient DescentJinho Choi Gradient descent is an optimization algorithm used in supervised learning problems to minimize a loss function. It works by taking steps in the negative direction of the gradient of the loss function with respect to the weights at each iteration. Stochastic gradient descent is a variant that updates the weights for each training example, rather than for the full batch. The perceptron is an algorithm that updates the weights only when the prediction is incorrect. It converges when the weights correctly classify all training examples.
Using Gradient Descent for Optimization and Learning



Using Gradient Descent for Optimization and LearningDr. Volkan OBAN This document discusses optimization techniques for gradient descent, including the basics of gradient descent, Newton's method, and quasi-Newton methods. It covers limitations of gradient descent and Newton's method, and approximations like Gauss-Newton, Levenberg-Marquardt, BFGS, and L-BFGS. It also discusses stochastic optimization techniques for handling large datasets with minibatch or online updates rather than full batch updates.
More Related Content
What's hot (20)
Optimization/Gradient Descent



Optimization/Gradient Descentkandelin The document discusses optimization and gradient descent algorithms. Optimization aims to select the best solution given some problem, like maximizing GPA by choosing study hours. Gradient descent is a method for finding the optimal parameters that minimize a cost function. It works by iteratively updating the parameters in the opposite direction of the gradient of the cost function, which points in the direction of greatest increase. The process repeats until convergence. Issues include potential local minimums and slow convergence.
Linear regression



Linear regressionMartinHogg9 A summary of what I learned about Linear Regression from the excellent Lazy Programmer Courses at https://lazyprogrammer.me
Decision tree



Decision treeR A Akerkar This document provides an overview of decision trees, including:
- Decision trees classify records by sorting them down the tree from root to leaf node, where each leaf represents a classification outcome.
- Trees are constructed top-down by selecting the most informative attribute to split on at each node, usually based on information gain.
- Trees can handle both numerical and categorical data and produce classification rules from paths in the tree.
- Examples of decision tree algorithms like ID3 that use information gain to select the best splitting attribute are described. The concepts of entropy and information gain are defined for selecting splits.
Linear regression with gradient descent



Linear regression with gradient descentSuraj Parmar Intro to the very popular optimization Technique(Gradient descent) with linear regression . Linear regression with Gradient descent on www.landofai.com
Concept learning and candidate elimination algorithm



Concept learning and candidate elimination algorithmswapnac12 This document discusses concept learning, which involves inferring a Boolean-valued function from training examples of its input and output. It describes a concept learning task where each hypothesis is a vector of six constraints specifying values for six attributes. The most general and most specific hypotheses are provided. It also discusses the FIND-S algorithm for finding a maximally specific hypothesis consistent with positive examples, and its limitations in dealing with noise or multiple consistent hypotheses. Finally, it introduces the candidate-elimination algorithm and version spaces as an improvement over FIND-S that can represent all consistent hypotheses.
Bayes Classification



Bayes Classificationsathish sak Uncertainty & Probability
Baye's rule
Choosing Hypotheses- Maximum a posteriori
Maximum Likelihood - Baye's concept learning
Maximum Likelihood of real valued function
Bayes optimal Classifier
Joint distributions
Naive Bayes Classifier
Feed forward ,back propagation,gradient descent



Feed forward ,back propagation,gradient descentMuhammad Rasel This document discusses gradient descent algorithms, feedforward neural networks, and backpropagation. It defines machine learning, artificial intelligence, and deep learning. It then explains gradient descent as an optimization technique used to minimize cost functions in deep learning models. It describes feedforward neural networks as having connections that move in one direction from input to output nodes. Backpropagation is mentioned as an algorithm for training neural networks.
Lecture 6: Ensemble Methods 



Lecture 6: Ensemble Methods Marina Santini What is an "ensemble learner"? How can we combine different base learners into an ensemble in order to improve the overall classification performance? In this lecture, we are providing some answers to these questions.
Inductive bias



Inductive biasswapnac12 This document discusses inductive bias in machine learning. It defines inductive bias as the assumptions that allow an inductive learning system to generalize beyond its training data. Without some biases, a learning system cannot rationally classify new examples. The document compares different learning algorithms based on the strength of their inductive biases, from weak biases like rote learning to stronger biases like preferring more specific hypotheses. It argues that all inductive learning systems require some inductive biases to generalize at all.
Decision Tree Learning



Decision Tree LearningMilind Gokhale This presentation was prepared as part of the curriculum studies for CSCI-659 Topics in Artificial Intelligence Course - Machine Learning in Computational Linguistics.
It was prepared under guidance of Prof. Sandra Kubler.
Machine Learning: Bias and Variance Trade-off



Machine Learning: Bias and Variance Trade-offInternational Institute of Information Technology (I²IT) Machine learning models involve a bias-variance tradeoff, where increased model complexity can lead to overfitting training data (high variance) or underfitting (high bias). Bias measures how far model predictions are from the correct values on average, while variance captures differences between predictions on different training data. The ideal model has low bias and low variance, accurately fitting training data while generalizing to new examples.
Support Vector Machine ppt presentation



Support Vector Machine ppt presentationAyanaRukasar Support vector machines (SVM) is a supervised machine learning algorithm used for both classification and regression problems. However, it is primarily used for classification. The goal of SVM is to create the best decision boundary, known as a hyperplane, that separates clusters of data points. It chooses extreme data points as support vectors to define the hyperplane. SVM is effective for problems that are not linearly separable by transforming them into higher dimensional spaces. It works well when there is a clear margin of separation between classes and is effective for high dimensional data. An example use case in Python is presented.
Support vector machine



Support vector machinezekeLabs Technologies Support vector machines are a type of supervised machine learning algorithm used for classification and regression analysis. They work by mapping data to high-dimensional feature spaces to find optimal linear separations between classes. Key advantages are effectiveness in high dimensions, memory efficiency using support vectors, and versatility through kernel functions. Hyperparameters like kernel type, gamma, and C must be tuned for best performance. Common kernels include linear, polynomial, and radial basis function kernels.
Linear Regression Algorithm | Linear Regression in Python | Machine Learning ...



Linear Regression Algorithm | Linear Regression in Python | Machine Learning ...Edureka! The document discusses linear regression algorithms. It begins with an introduction to regression analysis and its uses. Then it differentiates between linear and logistic regression. Next, it defines linear regression and discusses how to find the best fit regression line using the least squares method. It also explains how to check the goodness of fit using the R-squared method. Finally, it provides an overview of implementing linear regression using Python libraries.
Bias and variance trade off



Bias and variance trade offVARUN KUMAR This manuscript addresses the fundamentals of the trade-off relation between bias and variance in machine learning.
Activation function



Activation functionAstha Jain Artificial neural networks mimic the human brain by using interconnected layers of neurons that fire electrical signals between each other. Activation functions are important for neural networks to learn complex patterns by introducing non-linearity. Without activation functions, neural networks would be limited to linear regression. Common activation functions include sigmoid, tanh, ReLU, and LeakyReLU, with ReLU and LeakyReLU helping to address issues like vanishing gradients that can occur with sigmoid and tanh functions.
Lasso and ridge regression



Lasso and ridge regressionSreerajVA The document discusses different types of linear regression models including simple linear regression, multiple linear regression, ridge regression, lasso regression, and elastic net regression. It explains the concepts of slope, intercept, underfitting, overfitting, and regularization techniques used to constrain model weights. Specifically, it describes how ridge regression uses an L2 penalty, lasso regression uses an L1 penalty, and elastic net uses a combination of L1 and L2 penalties to regularize linear regression models and reduce overfitting.
Naïve Bayes Classifier Algorithm.pptx



Naïve Bayes Classifier Algorithm.pptxShubham Jaybhaye The document provides an overview of the Naive Bayes algorithm for classification problems. It begins by explaining that Naive Bayes is a supervised learning algorithm based on Bayes' theorem. It then explains the key aspects of Naive Bayes:
- It assumes independence between features (naive) and uses Bayes' theorem to calculate probabilities (Bayes).
- Bayes' theorem is used to calculate the probability of a hypothesis given observed data.
- An example demonstrates how Naive Bayes classifies weather data to predict whether to play or not play.
The document concludes by discussing the advantages, disadvantages, applications, and types of Naive Bayes models, as well as providing Python code to implement a Naive Bayes classifier.
Machine learning Lecture 2



Machine learning Lecture 2Srinivasan R The document summarizes key concepts in machine learning including concept learning as search, general-to-specific learning, version spaces, candidate elimination algorithm, and decision trees. It discusses how concept learning can be viewed as searching a hypothesis space to find the hypothesis that best fits the training examples. The candidate elimination algorithm represents the version space using the most general and specific hypotheses to efficiently learn from examples.
Instance Based Learning in Machine Learning



Instance Based Learning in Machine LearningPavithra Thippanaik Slides were formed by referring to the text Machine Learning by Tom M Mitchelle (Mc Graw Hill, Indian Edition) and by referring to Video tutorials on NPTEL
Machine Learning: Bias and Variance Trade-off



Machine Learning: Bias and Variance Trade-offInternational Institute of Information Technology (I²IT)
Viewers also liked (20)
CS571: Gradient Descent



CS571: Gradient DescentJinho Choi Gradient descent is an optimization algorithm used in supervised learning problems to minimize a loss function. It works by taking steps in the negative direction of the gradient of the loss function with respect to the weights at each iteration. Stochastic gradient descent is a variant that updates the weights for each training example, rather than for the full batch. The perceptron is an algorithm that updates the weights only when the prediction is incorrect. It converges when the weights correctly classify all training examples.
Using Gradient Descent for Optimization and Learning



Using Gradient Descent for Optimization and LearningDr. Volkan OBAN This document discusses optimization techniques for gradient descent, including the basics of gradient descent, Newton's method, and quasi-Newton methods. It covers limitations of gradient descent and Newton's method, and approximations like Gauss-Newton, Levenberg-Marquardt, BFGS, and L-BFGS. It also discusses stochastic optimization techniques for handling large datasets with minibatch or online updates rather than full batch updates.
Gradient Descent, Back Propagation, and Auto Differentiation - Advanced Spark...



Gradient Descent, Back Propagation, and Auto Differentiation - Advanced Spark...Chris Fregly Advanced Spark and TensorFlow Meetup 08-04-2016
Fundamental Algorithms of Neural Networks including Gradient Descent, Back Propagation, Auto Differentiation, Partial Derivatives, Chain Rule
07 logistic regression and stochastic gradient descent



07 logistic regression and stochastic gradient descentSubhas Kumar Ghosh This document provides an overview of logistic regression using stochastic gradient descent. It explains that logistic regression can be used for classification problems where the output is discrete. The key aspects covered include:
- Logistic regression estimates the logit (log odds) of the probability rather than the probability directly, using a linear function of the input features.
- It learns a hyperplane that separates the classes by choosing weights to maximize the likelihood of the training data.
- Stochastic gradient descent can be used as an optimization technique to learn the weights by minimizing the negative log likelihood.
- An example is provided of using the Mahout machine learning library to build a logistic regression model for classification using features from a donut-
Neiwpcc2010.ppt



Neiwpcc2010.pptJohn B. Cook, PE, CEO This document discusses using data mining techniques like artificial neural networks (ANN) to model the impacts of nonpoint source pollution in complex coastal estuaries. ANN models can extract relationships from large monitoring datasets to better understand estuary dynamics and the effects of factors like rainfall, tides, and freshwater flows. Case studies of the Cooper River and Beaufort River estuaries show ANN models accurately simulate dissolved oxygen levels and salinity intrusion in response to these drivers. Data mining allows interactive "what if" scenarios to inform total maximum daily load and permitting decisions.
Stochastic gradient descent and its tuning



Stochastic gradient descent and its tuningArsalan Qadri This paper talks about optimization algorithms used for big data applications. We start with explaining the gradient descent algorithms and its limitations. Later we delve into the stochastic gradient descent algorithms and explore methods to improve it it by adjusting learning rates.
Art2



Art2ESCOM Adaptive Resonance Theory (ART) is an unsupervised neural network designed to overcome the stability-plasticity dilemma. ART networks can dynamically classify input data into stable clusters while remaining plastic to learn new clusters. ART-1 specifically handles binary input vectors using a fast, self-organizing hypothesis testing cycle between short-term memory layers F1 and F2. The vigilance parameter controls how closely top-down expectations from F2 must match bottom-up input patterns from F1 before F2 resets and the cycle repeats to find a better match.
CS571: Sentiment Analysis



CS571: Sentiment AnalysisJinho Choi Sentiment analysis is a natural language processing task that identifies the sentiment of a document, such as whether a sentence, tweet, blog, or article expresses a positive or negative opinion. Machine learning approaches like n-gram models represent documents as collections of n-grams and use them to train classifiers like Naive Bayes, Maximum Entropy, and Support Vector Machines that can identify sentiment with over 80% accuracy. However, sentiment analysis still faces challenges in handling negation, mixtures of sentiment, ambiguity, and identifying sentiment towards specific aspects.
Lecture29



Lecture29Dr Sandeep Kumar Poonia The document discusses local search methods and metaheuristics for optimization problems. It introduces genetic algorithms, ant algorithms, particle swarm optimization, and bee algorithms as metaheuristics inspired by natural processes. Local search methods are described as iterative improvement approaches that start with an initial solution and move to neighboring solutions. Metaheuristics are higher-level procedures that guide heuristic optimization algorithms to search for optimal or near-optimal solutions. The document also discusses deterministic and stochastic search methods.
Adaptive filtersfinal



Adaptive filtersfinalWiw Miu The document describes adaptive filters and the least mean squares (LMS) algorithm. Adaptive filters are filters whose coefficients are adjusted over time based on an optimization algorithm to minimize a cost function. The LMS algorithm is commonly used to update the filter coefficients to minimize the mean squared error between the filter output and a desired response. It does this by iteratively adjusting each coefficient proportional to the input signal and the error at each time step in an efficient way that does not require knowledge of complete statistics. The LMS algorithm and its application are summarized.
Reducting Power Dissipation in Fir Filter: an Analysis



Reducting Power Dissipation in Fir Filter: an AnalysisCSCJournals This document summarizes and analyzes three existing techniques for reducing power consumption in FIR filters: signed power-of-two representation, steepest descent optimization, and coefficient segmentation. It finds that steepest descent can reduce hamming distance between coefficients by up to 26%, while coefficient segmentation can achieve up to 47% reduction. However, both techniques degrade filter performance parameters slightly. Signed power-of-two representation provides the most power reduction of 63% but introduces overhead from additional adders and shifters. The document evaluates these techniques on four low-pass FIR filters and concludes there is a tradeoff between hamming distance reduction and degradation of filter specifications.
Machine learning with Apache Hama



Machine learning with Apache HamaTommaso Teofili This document discusses machine learning with Apache Hama, a Bulk Synchronous Parallel computing framework. It provides an overview of Apache Hama and BSP, explains why machine learning algorithms are well-suited for BSP, and gives examples of collaborative filtering, k-means clustering, and gradient descent implemented on Hama. Benchmark results show Hama performs comparably to Apache Mahout for these algorithms.
02.03 Artificial Intelligence: Search by Optimization



02.03 Artificial Intelligence: Search by OptimizationAndres Mendez-Vazquez This a set of slides explaining the search methods by
Gradient Descent
Simulated Annealing
Hill Climbing
They are still not great, but they are good enough
A Multiple-Shooting Differential Dynamic Programming Algorithm



A Multiple-Shooting Differential Dynamic Programming AlgorithmEtienne Pellegrini Presentation given at the AAS/AIAA Space Flight Mechanics Meeting in San Antonio, TX, on 2/6/17. Paper available here: https://www.researchgate.net/publication/315444784_A_Multiple-Shooting_Differential_Dynamic_Programming_Algorithm
Multiple-shooting benefits a wide variety of optimal control algorithms, by alleviating large sensitivities present in highly nonlinear problems, improving robustness to initial guesses, and increasing the potential for a parallel implementation. In this work, the multiple shooting approach is embedded for the first time in the formulation of a differential dynamic programming algorithm. The necessary theoretical developments are presented for a DDP algorithm based on augmented Lagrangian techniques, using an outer loop to update the Lagrange multipliers, and an inner loop to optimize the controls of independent legs and select the multiple-shooting initial conditions. Numerical results are shown for several optimal control problems, including the low-thrust orbit transfer problem.
Statistical Learning and Text Classification with NLTK and scikit-learn



Statistical Learning and Text Classification with NLTK and scikit-learnOlivier Grisel Introduction to text document classification in python with 2 samples open source projects: NLTK and scikit-learn.
Optimization of Cairo West Power Plant for Generation



Optimization of Cairo West Power Plant for GenerationHossam Zein Optimization of Cairo West Power Plant for Generation
Case STUDY
BY . Hossam Ahmed Zein
Optmization techniques



Optmization techniquesDeepshika Reddy OPTIMIZATION TECHNIQUES
Optimization techniques are methods for achieving the best possible result under given constraints. There are various classical and advanced optimization methods. Classical methods include techniques for single-variable, multi-variable without constraints, and multi-variable with equality or inequality constraints using methods like Lagrange multipliers or Kuhn-Tucker conditions. Advanced methods include hill climbing, simulated annealing, genetic algorithms, and ant colony optimization. Optimization has applications in fields like engineering, business/economics, and pharmaceutical formulation to improve processes and outcomes under constraints.
Outdoor propagatiom model



Outdoor propagatiom modelKrishnapavan Samudrala The document discusses several outdoor propagation models used to predict radio signal strength over long distances. It focuses on the Longley-Rice and Okumura models. The Longley-Rice model predicts transmission loss using terrain profiles and diffraction losses from obstacles. It is available as a computer program that inputs frequency, path length, antenna heights and terrain parameters. The Okumura model uses curves to predict median signal attenuation relative to free space over distances from 1-100 km based on frequency, distance from base station, and terrain factors. It is widely used for cellular predictions in urban environments.
Ad
Similar to Gradient descent method (20)
Lecture_3_Gradient_Descent.pptx



Lecture_3_Gradient_Descent.pptxgnans Kgnanshek The document provides an overview of gradient descent and subgradient descent algorithms for minimizing convex functions. It discusses:
- Gradient descent takes steps in the direction of the negative gradient to minimize a differentiable function.
- Subgradient descent is similar but uses subgradients to minimize non-differentiable convex functions.
- Step sizes and stopping criteria like line search are important for convergence. Diminishing step sizes are needed for subgradient descent convergence.
Gradient_Descent_Unconstrained.pdf



Gradient_Descent_Unconstrained.pdfMTrang34 - The document discusses the convergence rate of gradient descent for minimizing strongly convex and smooth loss functions.
- It shows that under suitable step sizes, the gradient descent iterates converge geometrically fast to the optimal solution.
- It then applies this analysis to the generalized linear model, showing that gradient descent can estimate the true parameter within radius proportional to the statistical error, provided enough iterations.
Methods for Non-Linear Least Squares Problems



Methods for Non-Linear Least Squares Problemsapariciovenegas28 Guía práctica sobre métodos numéricos para resolver problemas de mínimos cuadrados no lineales. Presenta algoritmos como Gauss-Newton, Levenberg-Marquardt y variantes modernas, enfocándose en su implementación eficiente y en la evaluación de su rendimiento. Está dirigido a ingenieros, matemáticos aplicados y programadores científicos que trabajan con modelos de ajuste de datos. El enfoque es técnico y práctico, con ejemplos y recomendaciones sobre cómo enfrentar desafíos comunes en este tipo de problemas.
CI_L01_Optimization.pdf



CI_L01_Optimization.pdfSantiagoGarridoBulln This document discusses several classical methods for unconstrained continuous optimization, including gradient descent, Newton's method, the Gauss-Newton method, and the Levenberg-Marquardt algorithm. It explains how each method works by choosing a search direction to iteratively minimize an objective function. Newton's method and the Gauss-Newton method have faster convergence than gradient descent but require computing Hessians. The Levenberg-Marquardt algorithm interpolates between gradient descent and Gauss-Newton steps to improve convergence.
Optim_methods.pdf



Optim_methods.pdfSantiagoGarridoBulln The document discusses various optimization methods for minimizing objective functions. It covers continuous, discrete, and combinatorial optimization problems. Common approaches to optimization include analytical, graphical, experimental, and numerical methods. Specific techniques discussed include gradient descent, Newton's method, conjugate gradient descent, and quasi-Newton methods. The document also covers linear programming, integer programming, and nonlinear programming.
Strong convexity on gradient descent and newton's method



Strong convexity on gradient descent and newton's methodSEMINARGROOT Gradient descent is an optimization algorithm used to find local minima of differentiable functions. It works by taking steps in the negative direction of the gradient of the function at the current point. Newton's method approximates the function using a second-order Taylor expansion and finds the minimum of the quadratic approximation to determine the next step. The gradient descent step size can be shown to decrease the function value when the function is strongly convex or satisfies the Lipschitz condition.
Optimization tutorial



Optimization tutorialNorthwestern University This document provides an overview of optimization techniques. It defines optimization as identifying variable values that minimize or maximize an objective function subject to constraints. It then discusses various applications of optimization in finance, engineering, and data modeling. The document outlines different types of optimization problems and algorithms. It provides examples of unconstrained optimization algorithms like gradient descent, conjugate gradient, Newton's method, and BFGS. It also discusses the Nelder-Mead simplex algorithm for constrained optimization and compares the performance of these algorithms on sample problems.
cos323_s06_lecture03_optimization.ppt



cos323_s06_lecture03_optimization.pptdevesh604174 Lockhart and Johnson (1996) define optimization as “the process of finding the most effective or favorable value or condition” (p. 610). The purpose of optimization is to achieve the “best” design relative to a set of prioritized criteria or constraints.Within the traditional engineering disciplines, optimization techniques are commonly employed for a variety of problems, including: Product-Mix Problems. Determine the mix of products in a factory that will make the best use of machines, labor resources, raw materials, while maximizing the companies profitsOptimization involves the selection of the “best” solution from among the set of candidate solutions. The degree of goodness of the solution is quantified using an objective function (e.g., cost) which is to be minimized or maximized.Optimization problem: Maximizing or minimizing some function relative to some set,
often representing a range of choices available in a certain situation. The function
allows comparison of the different choices for determining which might be “best.”
Common applications: Minimal cost, maximal profit, minimal error, optimal design,
optimal management, variational principles.
Goals of the subject: The understanding of
Modeling issues—
What to look for in setting up an optimization problem?
What features are advantageous or disadvantageous?
What devices/tricks of formulation are available?
How can problems usefully be categorized?
Analysis of solutions—
What is meant by a “solution?”
When do solutions exist, and when are they unique?
How can solutions be recognized and characterized?
What happens to solutions under perturbations?
Numerical methods—
How can solutions be determined by iterative schemes of computation?
What modes of local simplification of a problem are convenient/appropriate?
How can different solution techniques be compared and evaluated?Distinguishing features of optimization as a mathematical discipline:
descriptive −→ prescriptive
equations −→ inequalities
linear/nonlinear −→ convex/nonconvex
differential calculus −→ subdifferential calculus
1
Finite-dimensional optimization: The case where a choice corresponds to selecting
the values of a finite number of real variables, called decision variables. For general
purposes the decision variables may be denoted by x1, . . . , xn and each possible choice
therefore identified with a point x = (x1, . . . , xn) in the space IRn
. This is what we’ll
be focusing on in this course.
Feasible set: The subset C of IRn
representing the allowable choices x = (x1, . . . , xn).
Objective function: The function f0(x) = f0(x1, . . . , xn) that is to be maximized or
minimized over C.
Constraints: Side conditions that are used to specify the feasible set C within IRn
.
Equality constraints: Conditions of the form fi(x) = ci
for certain functions fi on IRn
and constants ci
in IRn
.
Inequality constraints: Conditions of the form fi(x) ≤ ci or fi(x) ≥ ci
for certain
functions fi on IRn
and constants ci
in IR.
Range constarintt
AOT3 Multivariable Optimization Algorithms.pdf



AOT3 Multivariable Optimization Algorithms.pdfSandipBarik8 This document provides an overview of multi-variable optimization algorithms. It discusses two broad categories of multi-variable optimization methods: direct search methods and gradient-based methods. For gradient-based methods, it describes Cauchy's steepest descent method, in which the search direction at each iteration is the negative of the gradient to find the direction of maximum descent. It also introduces the simplex search method as a direct search method that manipulates a set of points to iteratively create better solutions without using gradients.
Regression_1.pdf



Regression_1.pdfAmir Saleh 1. Regression is a supervised learning technique used to predict continuous valued outputs. It can be used to model relationships between variables to fit a linear equation to the training data.
2. Gradient descent is an iterative algorithm that is used to find the optimal parameters for a regression model by minimizing the cost function. It works by taking steps in the negative gradient direction of the cost function to converge on the local minimum.
3. The learning rate determines the step size in gradient descent. A small learning rate leads to slow convergence while a large rate may oscillate and fail to converge. Gradient descent automatically takes smaller steps as it approaches the local minimum.
Optimization



OptimizationNaveen Saggu This document discusses optimization techniques for finding the minimum or maximum of an objective function subject to constraints. It begins by defining the key components of an optimization problem - the objective function, variables, and constraints. It then covers 1D optimization methods like golden section search and Newton's method, as well as multi-dimensional techniques including Newton's method, gradient descent, conjugate gradient, and the Nelder-Mead simplex method. The document also briefly discusses constrained optimization problems.
2. Linear regression with one variable.pptx



2. Linear regression with one variable.pptxEmad Nabil This document discusses linear regression with one variable. It introduces the model representation and hypothesis for linear regression. The goal of supervised learning is to output a hypothesis function h that takes input features and predicts the output based on training data. For linear regression, h is a linear equation representing the linear relationship between one input feature (e.g. house size) and the output (e.g. price). The cost function aims to minimize errors by finding optimal parameters θ0 and θ1. Gradient descent is used to iteratively update the parameters to minimize the cost function and find the optimal linear fit for the training data.
Steepest descent method



Steepest descent methodProf. Neeta Awasthy This document discusses the steepest descent method, also called gradient descent, for finding the nearest local minimum of a function. It works by iteratively moving from each point in the direction of the negative gradient to minimize the function. While effective, it can be slow for functions with long, narrow valleys. The step size used in gradient descent is important - too large will diverge it, too small will take a long time to converge. The Lipschitz constant of a function's gradient provides an upper bound for the step size to guarantee convergence.
Linear regression, costs & gradient descent



Linear regression, costs & gradient descentRevanth Kumar Linear Regression is a predictive model to map the relation between the dependent variable and one or more independent variables.
lecture6.ppt



lecture6.pptAbhiYadav655132 Newton's method and Gauss-Newton method can be used to minimize a nonlinear least squares function to fit a vector of model parameters to a data vector. The Gauss-Newton method approximates the Hessian matrix as the Jacobian transpose times the Jacobian, ignoring additional terms, making it faster to compute but less accurate than Newton's method. The Levenberg-Marquardt method interpolates between Gauss-Newton and steepest descent methods to provide a balance of convergence speed and accuracy. Iterative methods like conjugate gradients are useful for large nonlinear problems where storing and inverting the full matrix would be prohibitive. L1 regression provides a more robust alternative to L2 regression for dealing with outliers through minimization of the absolute error rather
Optimum engineering design - Day 5. Clasical optimization methods



Optimum engineering design - Day 5. Clasical optimization methodsSantiagoGarridoBulln The document discusses various numerical optimization methods for solving unconstrained nonlinear problems. It covers iterative methods for finding the optimal solution, including techniques for determining a suitable search direction and performing a line search to minimize the objective function along that direction. Specific methods covered include the steepest descent method, conjugate gradient method, Newton's method, trust region methods, and line search techniques like the golden section search and quadratic approximation.
Coordinate Descent method



Coordinate Descent methodSanghyuk Chun The document provides an overview of the coordinate descent method for minimizing convex functions. It discusses how coordinate descent works by iteratively minimizing a function with respect to one variable at a time while holding others fixed. The summary also notes that coordinate descent converges to a stationary point for continuously differentiable functions and has advantages like easy implementation and ability to handle large-scale problems, though it may be slower than other methods near the optimum.
Steepest descent method in sc



Steepest descent method in scrajshreemuthiah The document summarizes the method of steepest descent, an algorithm for finding the nearest local minimum of a function. It starts at an initial point P(0) and iteratively moves to points P(i+1) by minimizing along the line extending from P(i) in the direction of the negative gradient. While it can converge for some functions, it may require many iterations for functions with long valleys. A conjugate gradient method may be preferable for such cases. The step size taken at each iteration is important - too large may not converge, too small will take a long time to converge.
Ad
Recently uploaded (20)
Multistream in SIP and NoSIP @ OpenSIPS Summit 2025



Multistream in SIP and NoSIP @ OpenSIPS Summit 2025Lorenzo Miniero Slides for my "Multistream support in the Janus SIP and NoSIP plugins" presentation at the OpenSIPS Summit 2025 event.
They describe my efforts refactoring the Janus SIP and NoSIP plugins to allow for the gatewaying of an arbitrary number of audio/video streams per call (thus breaking the current 1-audio/1-video limitation), plus some additional considerations on what this could mean when dealing with application protocols negotiated via SIP as well.
Protecting Your Sensitive Data with Microsoft Purview - IRMS 2025



Protecting Your Sensitive Data with Microsoft Purview - IRMS 2025Nikki Chapple Session | Protecting Your Sensitive Data with Microsoft Purview: Practical Information Protection and DLP Strategies
Presenter | Nikki Chapple (MVP| Principal Cloud Architect CloudWay) & Ryan John Murphy (Microsoft)
Event | IRMS Conference 2025
Format | Birmingham UK
Date | 18-20 May 2025
In this closing keynote session from the IRMS Conference 2025, Nikki Chapple and Ryan John Murphy deliver a compelling and practical guide to data protection, compliance, and information governance using Microsoft Purview. As organizations generate over 2 billion pieces of content daily in Microsoft 365, the need for robust data classification, sensitivity labeling, and Data Loss Prevention (DLP) has never been more urgent.
This session addresses the growing challenge of managing unstructured data, with 73% of sensitive content remaining undiscovered and unclassified. Using a mountaineering metaphor, the speakers introduce the “Secure by Default” blueprint—a four-phase maturity model designed to help organizations scale their data security journey with confidence, clarity, and control.
🔐 Key Topics and Microsoft 365 Security Features Covered:
Microsoft Purview Information Protection and DLP
Sensitivity labels, auto-labeling, and adaptive protection
Data discovery, classification, and content labeling
DLP for both labeled and unlabeled content
SharePoint Advanced Management for workspace governance
Microsoft 365 compliance center best practices
Real-world case study: reducing 42 sensitivity labels to 4 parent labels
Empowering users through training, change management, and adoption strategies
🧭 The Secure by Default Path – Microsoft Purview Maturity Model:
Foundational – Apply default sensitivity labels at content creation; train users to manage exceptions; implement DLP for labeled content.
Managed – Focus on crown jewel data; use client-side auto-labeling; apply DLP to unlabeled content; enable adaptive protection.
Optimized – Auto-label historical content; simulate and test policies; use advanced classifiers to identify sensitive data at scale.
Strategic – Conduct operational reviews; identify new labeling scenarios; implement workspace governance using SharePoint Advanced Management.
🎒 Top Takeaways for Information Management Professionals:
Start secure. Stay protected. Expand with purpose.
Simplify your sensitivity label taxonomy for better adoption.
Train your users—they are your first line of defense.
Don’t wait for perfection—start small and iterate fast.
Align your data protection strategy with business goals and regulatory requirements.
💡 Who Should Watch This Presentation?
This session is ideal for compliance officers, IT administrators, records managers, data protection officers (DPOs), security architects, and Microsoft 365 governance leads. Whether you're in the public sector, financial services, healthcare, or education.
🔗 Read the blog: https://nikkichapple.com/irms-conference-2025/
Supercharge Your AI Development with Local LLMs



Supercharge Your AI Development with Local LLMsFrancesco Corti In today's AI development landscape, developers face significant challenges when building applications that leverage powerful large language models (LLMs) through SaaS platforms like ChatGPT, Gemini, and others. While these services offer impressive capabilities, they come with substantial costs that can quickly escalate especially during the development lifecycle. Additionally, the inherent latency of web-based APIs creates frustrating bottlenecks during the critical testing and iteration phases of development, slowing down innovation and frustrating developers.
This talk will introduce the transformative approach of integrating local LLMs directly into their development environments. By bringing these models closer to where the code lives, developers can dramatically accelerate development lifecycles while maintaining complete control over model selection and configuration. This methodology effectively reduces costs to zero by eliminating dependency on pay-per-use SaaS services, while opening new possibilities for comprehensive integration testing, rapid prototyping, and specialized use cases.
Jira Administration Training – Day 1 : Introduction



Jira Administration Training – Day 1 : IntroductionRavi Teja This presentation covers the basics of Jira for beginners. Learn how Jira works, its key features, project types, issue types, and user roles. Perfect for anyone new to Jira or preparing for Jira Admin roles.
Cyber Security Legal Framework in Nepal.pptx



Cyber Security Legal Framework in Nepal.pptxGhimire B.R. The presentation is about the review of existing legal framework on Cyber Security in Nepal. The strength and weakness highlights of the major acts and policies so far. Further it highlights the needs of data protection act .
AI Trends - Mary Meeker



AI Trends - Mary MeekerRazin Mustafiz Source: https://www.bondcap.com/reports/tai
Securiport - A Border Security Company



Securiport - A Border Security CompanySecuriport Securiport is a border security systems provider with a progressive team approach to its task. The company acknowledges the importance of specialized skills in creating the latest in innovative security tech. The company has offices throughout the world to serve clients, and its employees speak more than twenty languages at the Washington D.C. headquarters alone.
The case for on-premises AI



The case for on-premises AIPrincipled Technologies Exploring the advantages of on-premises Dell PowerEdge servers with AMD EPYC processors vs. the cloud for small to medium businesses’ AI workloads
AI initiatives can bring tremendous value to your business, but you need to support your new AI workloads effectively. That means choosing the best possible infrastructure for your needs—and many companies are finding that the cloud isn’t right for them. According to a recent Rackspace survey of IT executives, 69 percent of companies have moved some of their applications on-premises from the cloud, with half of those citing security and compliance as the reason and 44 percent citing cost.
On-premises solutions provide a number of advantages. With full control over your security infrastructure, you can be certain that all compliance requirements remain firmly in the hands of your IT team. Opting for on-premises also gives you the ability to design your infrastructure to the precise needs of that team and your new AI workloads. Depending on the workload, you may also see performance benefits, along with more predictable costs. As you start to build your next AI initiative, consider an on-premises solution utilizing AMD EPYC processor-powered Dell PowerEdge servers.
STKI Israel Market Study 2025 final v1 version



STKI Israel Market Study 2025 final v1 versionDr. Jimmy Schwarzkopf nnual (33 years) study of the Israeli Enterprise / public IT market. Covering sections on Israeli Economy, IT trends 2026-28, several surveys (AI, CDOs, OCIO, CTO, staffing cyber, operations and infra) plus rankings of 760 vendors on 160 markets (market sizes and trends) and comparison of products according to support and market penetration.
Measuring Microsoft 365 Copilot and Gen AI Success



Measuring Microsoft 365 Copilot and Gen AI SuccessNikki Chapple Session | Measuring Microsoft 365 Copilot and Gen AI Success with Viva Insights and Purview
Presenter | Nikki Chapple 2 x MVP and Principal Cloud Architect at CloudWay
Event | European Collaboration Conference 2025
Format | In person Germany
Date | 28 May 2025
📊 Measuring Copilot and Gen AI Success with Viva Insights and Purview
Presented by Nikki Chapple – Microsoft 365 MVP & Principal Cloud Architect, CloudWay
How do you measure the success—and manage the risks—of Microsoft 365 Copilot and Generative AI (Gen AI)? In this ECS 2025 session, Microsoft MVP and Principal Cloud Architect Nikki Chapple explores how to go beyond basic usage metrics to gain full-spectrum visibility into AI adoption, business impact, user sentiment, and data security.
🎯 Key Topics Covered:
Microsoft 365 Copilot usage and adoption metrics
Viva Insights Copilot Analytics and Dashboard
Microsoft Purview Data Security Posture Management (DSPM) for AI
Measuring AI readiness, impact, and sentiment
Identifying and mitigating risks from third-party Gen AI tools
Shadow IT, oversharing, and compliance risks
Microsoft 365 Admin Center reports and Copilot Readiness
Power BI-based Copilot Business Impact Report (Preview)
📊 Why AI Measurement Matters: Without meaningful measurement, organizations risk operating in the dark—unable to prove ROI, identify friction points, or detect compliance violations. Nikki presents a unified framework combining quantitative metrics, qualitative insights, and risk monitoring to help organizations:
Prove ROI on AI investments
Drive responsible adoption
Protect sensitive data
Ensure compliance and governance
🔍 Tools and Reports Highlighted:
Microsoft 365 Admin Center: Copilot Overview, Usage, Readiness, Agents, Chat, and Adoption Score
Viva Insights Copilot Dashboard: Readiness, Adoption, Impact, Sentiment
Copilot Business Impact Report: Power BI integration for business outcome mapping
Microsoft Purview DSPM for AI: Discover and govern Copilot and third-party Gen AI usage
🔐 Security and Compliance Insights: Learn how to detect unsanctioned Gen AI tools like ChatGPT, Gemini, and Claude, track oversharing, and apply eDLP and Insider Risk Management (IRM) policies. Understand how to use Microsoft Purview—even without E5 Compliance—to monitor Copilot usage and protect sensitive data.
📈 Who Should Watch: This session is ideal for IT leaders, security professionals, compliance officers, and Microsoft 365 admins looking to:
Maximize the value of Microsoft Copilot
Build a secure, measurable AI strategy
Align AI usage with business goals and compliance requirements
🔗 Read the blog https://nikkichapple.com/measuring-copilot-gen-ai/
ELNL2025 - Unlocking the Power of Sensitivity Labels - A Comprehensive Guide....



ELNL2025 - Unlocking the Power of Sensitivity Labels - A Comprehensive Guide....Jasper Oosterveld Sensitivity labels, powered by Microsoft Purview Information Protection, serve as the foundation for classifying and protecting your sensitive data within Microsoft 365. Their importance extends beyond classification and play a crucial role in enforcing governance policies across your Microsoft 365 environment. Join me, a Data Security Consultant and Microsoft MVP, as I share practical tips and tricks to get the full potential of sensitivity labels. I discuss sensitive information types, automatic labeling, and seamless integration with Data Loss Prevention, Teams Premium, and Microsoft 365 Copilot.
TrustArc Webinar: Mastering Privacy Contracting



TrustArc Webinar: Mastering Privacy ContractingTrustArc As data privacy regulations become more pervasive across the globe and organizations increasingly handle and transfer (including across borders) meaningful volumes of personal and confidential information, the need for robust contracts to be in place is more important than ever.
This webinar will provide a deep dive into privacy contracting, covering essential terms and concepts, negotiation strategies, and key practices for managing data privacy risks.
Whether you're in legal, privacy, security, compliance, GRC, procurement, or otherwise, this session will include actionable insights and practical strategies to help you enhance your agreements, reduce risk, and enable your business to move fast while protecting itself.
This webinar will review key aspects and considerations in privacy contracting, including:
- Data processing addenda, cross-border transfer terms including EU Model Clauses/Standard Contractual Clauses, etc.
- Certain legally-required provisions (as well as how to ensure compliance with those provisions)
- Negotiation tactics and common issues
- Recent lessons from recent regulatory actions and disputes
Contributing to WordPress With & Without Code.pptx



Contributing to WordPress With & Without Code.pptxPatrick Lumumba Contributing to WordPress: Making an Impact on the Test Team—With or Without Coding Skills
WordPress survives on collaboration, and the Test Team plays a very important role in ensuring the CMS is stable, user-friendly, and accessible to everyone.
This talk aims to deconstruct the myth that one has to be a developer to contribute to WordPress. In this session, I will share with the audience how to get involved with the WordPress Team, whether a coder or not.
We’ll explore practical ways to contribute, from testing new features, and patches, to reporting bugs. By the end of this talk, the audience will have the tools and confidence to make a meaningful impact on WordPress—no matter the skill set.
6th Power Grid Model Meetup - 21 May 2025



6th Power Grid Model Meetup - 21 May 2025DanBrown980551 6th Power Grid Model Meetup
Join the Power Grid Model community for an exciting day of sharing experiences, learning from each other, planning, and collaborating.
This hybrid in-person/online event will include a full day agenda, with the opportunity to socialize afterwards for in-person attendees.
If you have a hackathon proposal, tell us when you register!
About Power Grid Model
The global energy transition is placing new and unprecedented demands on Distribution System Operators (DSOs). Alongside upgrades to grid capacity, processes such as digitization, capacity optimization, and congestion management are becoming vital for delivering reliable services.
Power Grid Model is an open source project from Linux Foundation Energy and provides a calculation engine that is increasingly essential for DSOs. It offers a standards-based foundation enabling real-time power systems analysis, simulations of electrical power grids, and sophisticated what-if analysis. In addition, it enables in-depth studies and analysis of the electrical power grid’s behavior and performance. This comprehensive model incorporates essential factors such as power generation capacity, electrical losses, voltage levels, power flows, and system stability.
Power Grid Model is currently being applied in a wide variety of use cases, including grid planning, expansion, reliability, and congestion studies. It can also help in analyzing the impact of renewable energy integration, assessing the effects of disturbances or faults, and developing strategies for grid control and optimization.
Introducing FME Realize: A New Era of Spatial Computing and AR



Introducing FME Realize: A New Era of Spatial Computing and ARSafe Software A new era for the FME Platform has arrived – and it’s taking data into the real world.
Meet FME Realize: marking a new chapter in how organizations connect digital information with the physical environment around them. With the addition of FME Realize, FME has evolved into an All-data, Any-AI Spatial Computing Platform.
FME Realize brings spatial computing, augmented reality (AR), and the full power of FME to mobile teams: making it easy to visualize, interact with, and update data right in the field. From infrastructure management to asset inspections, you can put any data into real-world context, instantly.
Join us to discover how spatial computing, powered by FME, enables digital twins, AI-driven insights, and real-time field interactions: all through an intuitive no-code experience.
In this one-hour webinar, you’ll:
-Explore what FME Realize includes and how it fits into the FME Platform
-Learn how to deliver real-time AR experiences, fast
-See how FME enables live, contextual interactions with enterprise data across systems
-See demos, including ones you can try yourself
-Get tutorials and downloadable resources to help you start right away
Whether you’re exploring spatial computing for the first time or looking to scale AR across your organization, this session will give you the tools and insights to get started with confidence.
UiPath Community Berlin: Studio Tips & Tricks and UiPath Insights



UiPath Community Berlin: Studio Tips & Tricks and UiPath InsightsUiPathCommunity Join the UiPath Community Berlin (Virtual) meetup on May 27 to discover handy Studio Tips & Tricks and get introduced to UiPath Insights. Learn how to boost your development workflow, improve efficiency, and gain visibility into your automation performance.
📕 Agenda:
- Welcome & Introductions
- UiPath Studio Tips & Tricks for Efficient Development
- Best Practices for Workflow Design
- Introduction to UiPath Insights
- Creating Dashboards & Tracking KPIs (Demo)
- Q&A and Open Discussion
Perfect for developers, analysts, and automation enthusiasts!
This session streamed live on May 27, 18:00 CET.
Check out all our upcoming UiPath Community sessions at:
👉 https://community.uipath.com/events/
Join our UiPath Community Berlin chapter:
👉 https://community.uipath.com/berlin/
European Accessibility Act & Integrated Accessibility Testing



European Accessibility Act & Integrated Accessibility TestingJulia Undeutsch Emma Dawson will guide you through two important topics in this session.
Firstly, she will prepare you for the European Accessibility Act (EAA), which comes into effect on 28 June 2025, and show you how development teams can prepare for it.
In the second part of the webinar, Emma Dawson will explore with you various integrated testing methods and tools that will help you improve accessibility during the development cycle, such as Linters, Storybook, Playwright, just to name a few.
Focus: European Accessibility Act, Integrated Testing tools and methods (e.g. Linters, Storybook, Playwright)
Target audience: Everyone, Developers, Testers
Create Your First AI Agent with UiPath Agent Builder



Create Your First AI Agent with UiPath Agent BuilderDianaGray10 Join us for an exciting virtual event where you'll learn how to create your first AI Agent using UiPath Agent Builder. This session will cover everything you need to know about what an agent is and how easy it is to create one using the powerful AI-driven UiPath platform. You'll also discover the steps to successfully publish your AI agent. This is a wonderful opportunity for beginners and enthusiasts to gain hands-on insights and kickstart their journey in AI-powered automation.
Improving Developer Productivity With DORA, SPACE, and DevEx



Improving Developer Productivity With DORA, SPACE, and DevExJustin Reock Ready to measure and improve developer productivity in your organization?
Join Justin Reock, Deputy CTO at DX, for an interactive session where you'll learn actionable strategies to measure and increase engineering performance.
Leave this session equipped with a comprehensive understanding of developer productivity and a roadmap to create a high-performing engineering team in your company.
Evaluation Challenges in Using Generative AI for Science & Technical Content



Evaluation Challenges in Using Generative AI for Science & Technical ContentPaul Groth Evaluation Challenges in Using Generative AI for Science & Technical Content.
Foundation Models show impressive results in a wide-range of tasks on scientific and legal content from information extraction to question answering and even literature synthesis. However, standard evaluation approaches (e.g. comparing to ground truth) often don't seem to work. Qualitatively the results look great but quantitive scores do not align with these observations. In this talk, I discuss the challenges we've face in our lab in evaluation. I then outline potential routes forward.
Gradient descent method
- 1. Gradient descent method 2013.11.10 SanghyukChun Many contents are from Large Scale Optimization Lecture 4 & 5 by Caramanis& Sanghavi Convex Optimization Lecture 10 by Boyd & Vandenberghe Convex Optimization textbook Chapter 9 by Boyd & Vandenberghe 1
- 2. Contents •Introduction •Example code & Usage •Convergence Conditions •Methods & Examples •Summary 2
- 3. Introduction Unconstraint minimization problem, Description, Pros and Cons 3
- 4. Unconstrained minimization problems •Recall: Constrained minimization problems •From Lecture 1, the formation of a general constrained convex optimization problem is as follows •min푓푥푠.푡.푥∈χ •Where 푓:χ→Ris convex and smooth •From Lecture 1, the formation of an unconstrained optimization problem is as follows •min푓푥 •Where 푓:푅푛→푅is convex and smooth •In this problem, the necessary and sufficient condition for optimal solution x0 is •훻푓푥=0푎푡푥=푥0 4
- 5. Unconstrained minimization problems •Minimize f(x) •When f is differentiable and convex, a necessary and sufficient condition for a point 푥∗to be optimal is훻푓푥∗=0 •Minimize f(x) is the same as fining solution of 훻푓푥∗=0 •Min f(x): Analytically solving the optimality equation •훻푓푥∗=0: Usually be solved by an iterative algorithm 5
- 6. Description of Gradient Descent Method •The idea relies on the fact that −훻푓(푥(푘))is a descent direction •푥(푘+1)=푥(푘)−η푘훻푓(푥(푘))푤푖푡ℎ푓푥푘+1<푓(푥푘) •Δ푥(푘)is the step, or search direction •η푘is the step size, or step length •Too small η푘will cause slow convergence •Too large η푘could cause overshoot the minima and diverge 6
- 7. Description of Gradient Descent Method •Algorithm (Gradient Descent Method) •given a starting point 푥∈푑표푚푓 •repeat 1.Δ푥≔−훻푓푥 2.Line search: Choose step size ηvia exact or backtracking line search 3.Update 푥≔푥+ηΔ푥 •untilstopping criterion is satisfied •Stopping criterion usually 훻푓(푥)2≤휖 •Very simple, but often very slow; rarely used in practice 7
- 8. Pros and Cons •Pros •Can be applied to every dimension and space (even possible to infinite dimension) •Easy to implement •Cons •Local optima problem •Relatively slow close to minimum •For non-differentiable functions, gradient methods are ill-defined 8
- 9. Example Code & Usage Example Code, Usage, Questions 9
- 10. Gradient Descent Example Code •http://mirlab.org/jang/matlab/toolbox/machineLearning/ 10
- 11. Usage of Gradient Descent Method •Linear Regression •Find minimum loss function to choose best hypothesis 11 Example of Loss function: 푑푎푡푎푝푟푒푑푖푐푡−푑푎푡푎표푏푠푒푟푣푒푑 2 Find the hypothesis (function) which minimize the loss function
- 12. Usage of Gradient Descent Method •Neural Network •Back propagation •SVM (Support Vector Machine) •Graphical models •Least Mean Squared Filter …and many other applications! 12
- 13. Questions •Does Gradient Descent Method always converge? •If not, what is condition for convergence? •How can make Gradient Descent Method faster? •What is proper value for step size η푘 13
- 14. Convergence Conditions L-Lipschitzfunction, Strong Convexity, Condition number 14
- 15. L-Lipschitzfunction •Definition •A function 푓:푅푛→푅is called L-Lipschitzif and only if 훻푓푥−훻푓푦2≤퐿푥−푦2,∀푥,푦∈푅푛 •We denote this condition by 푓∈퐶퐿, where 퐶퐿is class of L-Lipschitzfunctions 15
- 16. L-Lipschitzfunction •Lemma 4.1 •퐼푓푓∈퐶퐿,푡ℎ푒푛푓푦−푓푥−훻푓푥,푦−푥≤ 퐿 2 푦−푥2 •Theorem 4.2 •퐼푓푓∈퐶퐿푎푛푑푓∗=min 푥 푓푥>−∞,푡ℎ푒푛푡ℎ푒푔푟푎푑푖푒푛푡푑푒푠푐푒푛푡 푎푙푔표푟푖푡ℎ푚푤푖푡ℎ푓푖푥푒푑푠푡푒푝푠푖푧푒푠푡푎푡푖푠푓푦푖푛푔η< 2 퐿 푤푖푙푙푐표푛푣푒푟푔푒푡표 푎푠푡푎푡푖표푛푎푟푦푝표푖푛푡 16
- 17. Strong Convexity and implications •Definition •If there exist a constant m > 0 such that 훻2푓≻=푚퐼푓표푟∀푥∈푆, then the function f(x) is strongly convex function on S 17
- 18. Strong Convexity and implications •Lemma 4.3 •If f is strongly convex on S, we have the following inequality: •푓푦≥푓푥+<훻푓푥,푦−푥>+ 푚 2 푦−푥2푓표푟∀푥,푦∈푆 •Proof 18 ( ) useful as stopping criterion (if you know m)
- 19. Strong Convexity and implications 19 Proof
- 20. Upper Bound of 훻2푓(푥) •Lemma 4.3 implies that the sublevel sets contained in S are bounded, so in particular, S is bounded. Therefore the maximum eigenvalue of 훻2푓푥is bounded above on S •ThereexistsaconstantMsuchthat훻2푓푥=≺푀퐼푓표푟∀푥∈푆 •Lemma 4.4 •퐹표푟푎푛푦푥,푦∈푆,푖푓훻2푓푥=≺푀퐼푓표푟푎푙푙푥∈푆푡ℎ푒푛 푓푦≤푓푥+<훻푓푥,푦−푥>+ 푀 2 푦−푥2 20
- 21. Condition Number •From Lemma 4.3 and 4.4 we have 푚퐼=≺훻2푓푥=≺푀퐼푓표푟∀푥∈푆,푚>0,푀>0 •The ratio k=M/m is thus an upper bound on the condition number of the matrix 훻2푓푥 •When the ratio is close to 1, we call it well-conditioned •When the ratio is much larger than 1, we call it ill-conditioned •When the ratio is exactly 1, it is the best case that only one step will lead to the optimal solution (there is no wrong direction) 21
- 22. Condition Number •Theorem 4.5 •Gradient descent for a strongly convex function f and step sizeη= 1 푀 will converge as •푓푥∗−푓∗≤푐푘푓푥0−푓∗,푤ℎ푒푟푒푐≤1− 푚 푀 •Rate of convergence c is known as linear convergence •Since we usually do not know the value of M, we do line search •For exact line search, 푐=1− 푚 푀 •For backtracking line search, 푐=1−min2푚훼,2훽훼푚 푀 <1 22
- 23. Methods & Examples Exact Line Search, Backtracking Line Search, Coordinate Descent Method, Steepest Descent Method 23
- 24. Exact Line Search • The optimal line search method in which η is chosen to minimize f along the ray 푥 − η훻푓 푥 , as shown in below • Exact line search is used when the cost of minimization problem with one variable is low compared to the cost of computing the search direction itself. • It is not very practical 24
- 25. Exact Line Search •Convergence Analysis • •푓푥푘−푓∗decreases by at least a constant factor in every iteration •Converging to 0 geometric fast. (linear convergence) 25 1
- 26. Backtracking Line Search •It depends on two constants 훼,훽푤푖푡ℎ0<훼<0.5,0<훽<1 •It starts with unit step size and then reduces it by the factor 훽until the stopping condition 푓(푥−η훻푓(푥))≤푓(푥)−훼η훻푓푥2 •Since −훻푓푥is a descent direction and −훻푓푥2<0, so for small enough step size η, we have 푓푥−η훻푓푥≈푓푥−η훻푓푥2<푓푥−훼η훻푓푥2 •It shows that the backtracking line search eventually terminates •훼is typically chosen between 0.01 and 0.3 •훽is often chosen to be between 0.1 and 0.8 26
- 27. Backtracking Line Search • 27
- 28. Backtracking Line Search •Convergence Analysis •Claim: η≤ 1 푀 always satisfies the stopping condition •Proof 28
- 29. Backtracking Line Search •Proof (cont) 29
- 30. Line search types •Slide from Optimization Lecture 10 by Boyd 30
- 31. Line search example •Slide from Optimization Lecture 10 by Boyd 31
- 32. Coordinate Descent Method • Coordinate descent belongs to the class of several non derivative methods used for minimizing differentiable functions. • Here, cost is minimized in one coordinate direction in each iteration. 32
- 33. Coordinate Descent Method •Pros •It is well suited for parallel computation •Cons •May not reach the local minimum even for convex function 33
- 34. Converge of Coordinate Descent •Lemma 5.4 34
- 35. Coordinate Descent Method •Method of selecting the coordinate for next iteration •Cyclic Coordinate Descent •Greedy Coordinate Descent •(Uniform) Random Coordinate Descent 35
- 36. Steepest Descent Method •The gradient descent method takes many iterations •Steepest Descent Method aims at choosing the best direction at each iteration •Normalized steepest descent direction •Δ푥푛푠푑=푎푟푔푚푖푛훻푓푥푇푣푣=1} •Interpretation: for small 푣,푓푥+푣≈푓푥+훻푓푥푇푣direction Δ푥푛푠푑 is unit-norm step with most negative directional derivative •Iteratively, the algorithm follows the following steps •Calculate direction of descent Δ푥푛푠푑 •Calculate step size, t •푥+=푥+푡Δ푥푛푠푑 36
- 37. Steepest Descent for various norms •The choice of norm used the steepest descent direction can be have dramatic effect on converge rate •푙2norm •The steepest descent direction is as follows •Δ푥푛푠푑= −훻푓(푥) 훻푓(푥)2 •푙1norm •For 푥1= 푖푥푖,a descent direction is as follows, •Δ푥푛푑푠=−푠푖푔푛 휕푓푥 휕푥푖 ∗푒푖 ∗ •푖∗=푎푟푔min 푖 휕푓 휕푥푖 •푙∞norm •For 푥∞=argmin 푖 푥푖,a descent direction is as follows •Δ푥푛푑푠=−푠푖푔푛−훻푓푥 37
- 38. Steepest Descent for various norms 38 Quadratic Norm 푙1-Norm
- 39. Steepest Descent for various norms •Example 39
- 40. Steepest Descent Convergence Rate •Fact: Any norm can be bounded by ∙2, i.e., ∃훾, 훾∈(0,1] such that, 푥≥훾푥2푎푛푑푥∗≥훾푥2 •Theorem 5.5 •If f is strongly convex with respect to m and M, and ∙2has 훾, 훾as above then steepest decent with backtracking line search has linear convergence with rate •푐=1−2푚훼 훾2min1, 훽훾 푀 •Proof: Will be proved in the lecture 6 40
- 41. Summary 41
- 42. Summary •Unconstrained Convex Optimization Problem •Gradient Descent Method •Step Size Trade-off between safety and speed •Convergence Conditions •L-LipschtizFunction •Strong Convexity •Condition Number 42
- 43. Summary •Exact Line Search •Backtracking Line Search •Coordinate Descent Method •Good for parallel computation but not always converge •Steepest Descent Method •The choice of norm is important 43
- 44. 44 END OF DOCUMENT





