[系列活動] Machine Learning 機器學習課程

Outline Introduction to Machine Learning Three Fundamental Algorithms Optimization Support Vector Machine Evaluation and
Machine Learning
Yuh-Jye Lee
Lab of Data Science and Machine Intelligence
Dept. of Applied Math. at NCTU
Feb. 12, 2017
1 / 136

1 Introduction to Machine Learning
Some Examples
Basic concept of learning theory
2 Three Fundamental Algorithms
3 Optimization
4 Support Vector Machine
5 Evaluation and Closed Remark
2 / 136

The Plan of My Lecture
Focus on Supervised Learning mainly (30minutes)
Many examples
Basic Concept of Learning Theorey
Will give you three basic algorithms (80minutes)
k-Nearest Neighbor
Naive Bayes Classiﬁer
Online Perceptron Algorithm
Brief Introduction to Optimization (90minutes)
Support Vector Machines (90minutes)
Evaluation and Closed Remarks (70minutes)
3 / 136

Some Examples
AlphaGo and Master
4 / 136

Some Examples
Mayhem Wins DARPA Cyber Grand Challenge
5 / 136

Some Examples
Supervised Learning Problems
Assumption: training instances are drawn from an unknown but fixed
probability distribution P(x, y) independently.
Our learning task:
Given a training set S = {(x1
, y1), (x2
, y2), . . . , (x , y )}
We would like to construct a rule, f (x) that can correctly
predict the label y given unseen x
If f (x) = y then we get some loss or penalty
For example: (f (x), y) = 1
2 |f (x) − y|
Learning examples: classification, regression and sequence labeling
If y is drawn from a finite set it will be a classification
problem. The simplest case: y ∈ {−1, + 1} called binary
classification problem
If y is a real number it becomes a regression problem
More general case, y can be a vector and each element is
drawn from a finite set. This is the sequence labeling problem
6 / 136

Some Examples
Binary Classiﬁcation Problem
(A Fundamental Problem in Data Mining)
Find a decision function (classiﬁer) to discriminate two
categories data set.
Supervised learning in Machine Learning
Decision Tree, Deep Neural Network, k-NN and Support
Vector Machines, etc.
Discrimination Analysis in Statistics
Fisher Linear Discriminator
Successful applications:
Cyber Security, Marketing, Bioinformatics, Fraud detection
7 / 136

Some Examples
Bankruptcy Prediction: Solvent vs. Bankrupt
A Binary Classification Problem
Deutsche Bank Dataset
40 financial indicators, (x part), from middle-market
capitalization 422 firms in Benelux.
74 firms went bankrupt and 348 were solvent. (y part)
The variables to be used in the model as explanatory inputs
are 40 financial indicators such as: liquidity, profitability and
solvency measurements.
Machine Learning will identify the most important indicators
W. Härdle, Y.-J. Lee, D. Schäfer, Dorothea and Y.-R. Yeh, “Variable
selection and oversampling in the use of smooth support vector machines
for predicting the default risk of companies”, Journal of Forecasting, vol
28, (6), p. 512 - 534, 2009
8 / 136

Some Examples
Given a training dataset
S = {(xi
, yi )|xi
∈ Rn
, yi ∈ {−1, 1}, i = 1, . . . , }
xi
∈ A+ ⇔ yi = 1 & xi
∈ A− ⇔ yi = −1
Main Goal:
Predict the unseen class label for new data
Estimate a posteriori probability of class label
Pr(y = 1|x) > Pr(y = −1|x) ⇒ x ∈ A+
Find a function f : Rn → R by learning from data
f (x) ≥ 0 ⇒ x ∈ A+ and f (x) < 0 ⇒ x ∈ A−
The simplest function is linear: f (x) = w x + b
9 / 136

Goal of Learning Algorithms
The early learning algorithms were designed to find such an
accurate fit to the data.
At that time, the training set size is relative small
A classifier is said to be consistent if it performed the correct
classification of the training data.
Please note that it is NOT our learning purpose
The ability of a classifier to correctly classify data not in the
training set is known as its generalization.
Bible code? 1994 Taipei Mayor election?
Predict the real future NOT fitting the data in your hand or
predict the desired results.
10 / 136

Three Fundamental Algorithms
Na¨ıve Bayes Classiﬁer
Based on Bayes’ Rule
k-Nearest Neighbors Algorithm
Distance and Instances based algorithm
Lazy learning
Online Perceptron Algorithm
Mistakes driven algorithm
The smallest unit of Deep Neural Networks
11 / 136

Conditional Probability
Deﬁnition
The conditional probability of an event A, given that an event B
has occurred, is equal to
P(A|B) =
P(A ∩ B)
P(B)
Example
Suppose that a fair die is tossed once. Find the probability of
a 1 (event A), given an odd number was obtained (event B).
P(A|B) =
P(A ∩ B)
P(B)
=
1/6
1/2
=
1
3
Restrict the sample space on the event B
12 / 136

Partition Theorem
Assume that {B1, B2, . . . , Bk} is a partition of S such that
P(Bi ) > 0, for i = 1, 2, . . . , k. Then
P(A) =
k
i=1
P(A|Bi )P(Bi ). A ∩ B1
A ∩ B2
A ∩ B3
B1
B2
B3
S
Note that {B1, B2, . . . , Bk} is a partition of S if
1 S = B1 ∪ B2 ∪ . . . ∪ Bk
2 Bi ∩ Bj = ∅ for i = j
13 / 136

Bayes’ Rule
Bayes’ Rule
Assume that {B1, B2, . . . , Bk} is a partition of S such that
P(Bi ) > 0, for i = 1, 2, . . . , k. Then
P(Bj |A) =
P(A|Bj )P(Bj )
k
i=1
P(A|Bi )P(Bi )
.
A ∩ B1
A ∩ B2
A ∩ B3
B1
B2
B3
S
14 / 136

Na¨ıve Bayes for Classiﬁcation
Also Good for Multi-class Classiﬁcation
Estimate a posteriori probability of class label
Let each attribute (variable) be a random variable. What is
the probibility of
Pr(y = 1|x) = Pr(y = 1|X1 = x1, X2 = x2, . . . , Xn = xn)
Na¨ıve Bayes TWO not reasonable assumptions:
The importance of each attribute is equal
All attributes are conditional probability independent !
Pr(y = 1|x) =
1
Pr(X = x)
n
i=1
Pr(y = 1|Xi = xi )
15 / 136

The Weather Data Example
Ian H. Witten & Eibe Frank, Data Mining
Outlook Temperature Humidity Windy Play(Label)
Sunny Hot High False -1
Sunny Hot High True -1
Overcast Hot High False +1
Rainy Mild High False +1
Rainy Cool Normal False +1
Rainy Cool Normal True -1
Overcast Cool Normal True +1
Sunny Mild High False -1
Sunny Cool Normal False +1
Rainy Mild Normal False +1
Sunny Mild Normal True +1
Overcast Mild High True +1
Overcast Hot Normal False +1
Rainy Mild High True -1
16 / 136

Probabilities for Weather Data
Using Maximum Likelihood Estimation
Outlook Temp. Humidity Windy Play
Play Yes No Yes No Yes No Yes No Yes No
Sunny
Overcast
Rainy
2/9
4/9
3/9
3/5
0/5
2/5
Hot
Mild
Cool
2/9
4/9
3/9
2/5
3/5
1/5
High
Normal
3/9
6/9
4/5
1/5
T
F
3/9
6/9
3/5
2/5
9/14 5/14
Likelihood of the two classes:
Pr(y = 1|sunny, cool, high, T) ∝
2
9
·
3
9
·
3
9
·
3
9
·
9
14
Pr(y = −1|sunny, cool, high, T) ∝
3
5
·
1
5
·
4
5
·
3
5
·
5
14
17 / 136

Zero-frequency Problem
What if an attribute value does NOT occur with a class
value?
The posterior probability will all be zero! No matter how likely
the other attribute values are!
Laplace estimator will ﬁx “zero-frequency”,
k + λ
n + aλ
Question: Roll a dice 8 times. The outcomes are as:
2, 5, 6, 2, 1, 5, 3, 6. What is the probability for showing 4?
Pr(X = 4) =
0 + λ
8 + 6λ
, Pr(X = 5) =
2 + λ
8 + 6λ
18 / 136

Instance-based Learning: k-nearest neighbor algorithm
Fundamental philosophy: Two instances that are close to each
other or similar to each other they should share with the
same label
Also known as memory-based learning since what they do is
store the training instances in a lookup table and interpolate
from these.
It requires memory of O(N)
Given an input similar ones should be found and ﬁnding them
requires computation of O(N)
Such methods are also called lazy learning algorithms.
Because they do NOT compute a model when they are given
a training set but postpone the computation of the model
until they are given a new test instance (query point)
19 / 136

k-Nearest Neighbors Classiﬁer
Given a query point xo, we ﬁnd the k training points
x(i), i = 1, 2, . . . , k closest in distance to xo
Then classify using majority vote among these k neighbors.
Choose k as an odd number will avoid the tie. Ties are broken
at random
If all attributes (features) are real-valued, we can use
Euclidean distance. That is d(x, xo) = x − xo
2
If the attribute values are discrete, we can use Hamming
distance, which counts the number of nonmatching attributes
d(x, xo
) =
n
j=1
1(xj = xo
j )
20 / 136

1-Nearest Neighbor Decision Boundary (Voronoi)
21 / 136

Distance Measure
Using different distance measurements will give very different
results in k-NN algorithm.
Be careful when you compute the distance
We might need to normalize the scale between different
attributes. For example, yearly income vs. daily spend
Typically we first standardize each of the attributes to have
mean zero and variance 1
ˆxj =
xj − µj
σj
22 / 136

Learning Distance Measure
Finding a distance function d(xi , xj ) such that if xi and xj are
belong to the class the distance is small and if they are
belong to the diﬀerent classes the distance is large.
Euclidean distance: xi − xj 2
2 = (xi − xj ) (xi − xj )
Mahalanobis distance: d(xi , xj ) = (xi − xj ) M(xi − xj ) where
M is a positive semi-deﬁnited matrix.
(xi
− xj
) M(xi
− xj
) = (xi
− xj
) L L(xi
− xj
)
= (Lxi
− Lxj
) (Lxi
− Lxj
)
The matrix L can be with the size k × n and k << n
23 / 136

Linear Learning Machines
The simplest function is linear: f (x) = w x + b
Finding this simplest function via an on-line and
mistake-driven procedure
Update the weight vector and bias when there is a
misclassiﬁed point
24 / 136

Linearly Separable Case
x w + b = 0
x w + b = −1
x w + b = +1
A-
Malignant
A+
Benign
w
25 / 136

Online Learning
Definition of online learning
Given a set of new training data,
Online learner can update its model without reading old data while
improving its performance.
In contrast, off-line learner must combine old and new data and start
the learning all over again, otherwise the performance will suffer.
Online is considered as a solution of large learning tasks
Usually require several passes (or epochs) through the training
instances
Need to keep all instances unless we only run the algorithm one
single pass
26 / 136

Perceptron Algorithm (Primal Form)
Rosenblatt, 1956
Given a training dataset S, and initial weight vector w0 = 0
and the bias b0 = 0
Repeat:
for i = 1 to
if yi ( wk · xi + bk) ≤ 0 then
wk+1 ← wk + ηyi xi
bk+1 ← bk + ηyi R2 R = max
1≤i≤
xi
k ← k + 1
end if
Until no mistakes made within the for loop
Return: k, (wk, bk).
What is k ?
27 / 136

yi( wk+1
· xi
+ bk+1) > yi( wk
· xi
) + bk ?
wk+1
←− wk
+ ηyixi
and bk+1 ←− bk + ηyiR2
yi ( wk+1
· xi
+ bk+1) = yi ( (wk
+ ηyi xi
) · xi
+ bk + ηyi R2
)
= yi ( wk
· xi
+ bk) + yi (ηyi ( xi
· xi
+ R2
))
= yi ( wk
· xi
+ bk) + η( xi
· xi
+ R2
)
R = max
1≤i≤
xi
28 / 136

Perceptron Algorithm Stop in Finite Steps
Theorem(Novikoﬀ)
Let S be a non-trivial training set, and let
R = max
1≤i≤
xi
Suppose that there exists a vector wopt such that wopt = 1 and
yi ( wopt · xi
+ bopt) ≥ γ for 1 ≤ i ≤ .
Then the number of mistakes made by the on-line perceptron
algorithm on S is almost (2R
γ )2.
29 / 136

Perceptron Algorithm (Dual Form)
w =
i=1
αiyixi
Given a linearly separable training set S and α = 0 , α ∈ R ,
b = 0 , R = max
1≤i≤
xi .
Repeat: for i = 1 to
if yi (
j=1
αj yj xj · xi + b) ≤ 0 then
αi ← αi + 1 ; b ← b + yi R2
end if
end for
Until no mistakes made within the for loop return: (α, b)
30 / 136

What We Got in the Dual Form of Perceptron Algorithm?
The number of updates equals:
i=1
αi = α 1 ≤ (2R
γ )2
αi > 0 implies that the training point (xi , yi ) has been
misclassified in the training process at least once.
αi = 0 implies that removing the training point (xi , yi ) will
not affect the final results.
The training data only appear in the algorithm through the
entries of the Gram matrix,G ∈ R × which is defined below:
Gij = xi , xj
The key idea of kernel trick in SVMs and all kernel methods
31 / 136

Outline
Some Examples
3 Optimization
32 / 136

You Have Learned (Unconstrained)
Optimization in Your High School
Let f (x) = ax2 + bx + c, a = 0, x∗ = − b
2a
Case 1 : f (x∗) = 2a > 0 ⇒ x∗ ∈ arg min
x∈R
f (x)
Case 2 : f (x∗) = 2a < 0 ⇒ x∗ ∈ arg max
x∈R
f (x)
For minimization problem (Case I),
f (x∗) = 0 is called the ﬁrst order optimality condition.
f (x∗) > 0 is the second order optimality condition.
33 / 136

Gradient and Hessian
Let f : Rn → R be a differentiable function. The gradient of
function f at a point x ∈ Rn is defined as
f (x) = [
∂f (x)
∂x1
,
∂f (x)
∂x2
, . . . ,
∂f (x)
∂xn
] ∈ Rn
If f : Rn → R is a twice differentiable function. The Hessian
matrix of f at a point x ∈ Rn is defined as
2
f (x) =




∂2f
∂x2
1
∂2f
∂x1∂x2
· · · ∂2f
∂x1∂xn
...
...
...
...
∂2f
∂xn∂x1
∂2f
∂xn∂x2
· · · ∂2f
∂x2
n



 ∈ Rn×n
34 / 136

Example of Gradient and Hessian
f (x) = x2
1 + x2
2 − 2x1 + 4x2
=
1
2
x1 x2
2 0
0 2
x1
x2
+ −2 4
x1
x2
f (x) = 2x1 − 2 2x2 + 4 , 2
f (x) =
2 0
0 2
By letting f (x) = 0, we have x∗ =
1
−2
∈ arg min
x∈R2
f (x)
35 / 136

Quadratic Functions (Standard Form)
f (x) = 1
2x Hx + p x
Let f : Rn → R and f (x) = 1
2x Hx + p x
where H ∈ Rn×n is a symmetric matrix and p ∈ Rn
then
f (x) = Hx + p
2
f (x) = H (Hessian)
Note: If H is positive deﬁnite, then x∗ = −H−1p is the unique
solution of min f (x).
36 / 136

Least-squares Problem
min
x∈Rn
Ax − b 2
2, A ∈ Rm×n
, b ∈ Rm
f (x) = (Ax − b) (Ax − b)
= x A Ax − 2b Ax + b b
f (x) = 2A Ax − 2A b
2
f (x) = 2A A
x∗
= (A A)−1
A b ∈ arg min
x∈Rn
Ax − b 2
2
If A A is nonsingular matrix ⇒ P.D.
Note : x∗ is an analytical solution.
37 / 136

How to Solve an Unconstrained MP
Get an initial point and iteratively decrease the obj. function
value.
Stop once the stopping criteria is satisﬁed.
Steep decent might not be a good choice.
Newtons method is highly recommended.
Local and quadratic convergent algorithm.
Need to choose a good step size to guarantee global
convergence.
38 / 136

The First Order Taylor Expansion
Let f : Rn → R be a diﬀerentiable function
f (x + d) = f (x) + f (x) d + α(x, d) d ,
where
lim
d→0
α(x, d) = 0
If f (x) d < 0 and d is small enough then f (x + d) < f (x).
We call d is a descent direction.
39 / 136

Steep Descent with Exact Line Search
Start with any x0 ∈ Rn. Having xi , stop if f (xi ) = 0.
Else compute xi+1 as follows:
1 Steep descent direction: di = − f (xi )
2 Exact line search: Choose a stepsize such that
df (xi + λdi )
dλ
= f (xi
+ λdi
) = 0
3 Updating: xi+1 = xi + λdi
40 / 136

MATLAB Code for Steep Descent with Exact Line Search
(Quadratic Function Only)
function [x, f value, iter] = grdlines(Q, p, x0, esp)
%
% min 0.5 ∗ x Qx + p x
% Solving unconstrained minimization via
% steep descent with exact line search
%
41 / 136

flag = 1;
iter = 0;
while flag > esp
grad = Qx0+p;
temp1 = grad’*grad;
if temp1 < 10−12
flag = esp;
else
stepsize = temp1/(grad’*Q*grad);
x1 = x0 - stepsize*grad;
flag = norm(x1-x0);
x0 = x1;
end;
iter = iter + 1;
end;
x = x0;
fvalue = 0.5*x’*Q*x+p’*x;
42 / 136

The Key Idea of Newton’s Method
Let f : Rn −→ R be a twice diﬀerentiable function
f (x + d) = f (x) + f (x) d +
1
2
d 2
f (x)d + β(x, d) d
where lim
d→0
β(x, d) = 0
At ith iteration, use a quadratic function to approximate
f (x) ≈ f (xi
) + f (xi
)(x − xi
) +
1
2
(x − xi
) 2
f (xi
)(x − xi
)
xi+1 = arg min ˜f (x)
43 / 136

Newton’s Method
Start with x0 ∈ Rn. Having xi ,stop if f (xi ) = 0
Else compute xi+1 as follows:
1 Newton direction: 2f (xi )di = − f (xi )
Have to solve a system of linear equations here!
2 Updating: xi+1 = xi + di
Converge only when x0
is close to x∗
enough.
44 / 136

It can not converge to the optimal solution.
f(x) = à 6
1
x6
+ 4
1
x4
+ 2x2
g(x) = f(xi
) + f0
(xi
)(x à xi
) + 2
1
f00
(xi
)(x à xi
)
f (x) = 1
6x6 + 1
4x4 + 2x2
g(x) = f (xi ) + f (xi )(x − xi ) + 1
2f (xi )(x − xi )2
It can not converge to the optimal solution.
45 / 136

People of ACM: David Blei, (Sept. 9, 2014)
The recipient of the 2013 ACM- Infosys Foundation Award in the
Computing Sciences, he is joining Columbia University this fall as a
Professor of Statistics and Computer Science, and will become a
member of Columbia’s Institute for Data Sciences and Engineering.
46 / 136

What is the most important recent innovation in machine
learning?
[A]: One of the main recent innovations in ML research has been
that we (the ML community) can now scale up our algorithms to
massive data, and I think that this has fueled the modern
renaissance of ML ideas in industry. The main idea is called
stochastic optimization, which is an adaptation of an old algorithm
invented by statisticians in the 1950s.
47 / 136

What is the most important recent innovation in machine
learning?
[A]: In short, many machine learning problems can be boiled down
to trying to ﬁnd parameters that maximize (or minimize) a
function. A common way to do this is “gradient ascent,”
iteratively following the steepest direction to climb a function to its
top. This technique requires repeatedly calculating the steepest
direction, and the problem is that this calculation can be
expensive. Stochastic optimization lets us use cheaper approximate
calculations. It has transformed modern machine learning.
48 / 136

Gradient Descent: Batch Learning
For an optimization problem
min f (w) = min r(w) +
1
i=1
(w; (xi
, yi ))
GD tries to ﬁnd a direction and the learning rate decreasing the objective
function value.
wt+1
= wt
− η f (wt
)
where η is the learning rate, − f (wt
) is the steepest direction
f (wt
) = r(wt
) +
1
i=1
(wt
; (xi
, yi ))
When is large, computing
i=1
(wt
; (xi
, yi )) may cost much time.
49 / 136

Stochastic Gradient Descent: Online Learning
In GD, we compute the gradient using the entire training set.
In stochastic gradient descent(SGD), we use
(wt
; (xt
, yt)) instead of
1
i=1
(wt
; (xi
, yi ))
So the gradient of f (wt
)
f (wt
) = r(wt
) + (wt
; (xt
, yt))
SGD computes the gradient using only one instance.
In experiment, SGD is signiﬁcantly faster than GD when is large.
50 / 136

Online Perceptron Algorithm [Rosenblatt, 1956]
The Perceptron is considered as a SGD method. The underlying
optimization problem of the algorithm
min
(w,b)∈Rn+1
i=1
(−yi ( w, xi + b))+
In the linearly separable case, the Perceptron alg. will be terminated
in finite steps no matter what learning rate is chosen
In the nonseparable case, how to decide the appropriate learning
rate that will make the least mistake is very difficult
Learning rate can be a nonnegative number. More general case, it
can be a positive definite matrix
51 / 136

What is Machine Learning?
Representation + Optimization + Evaluation
Pedro Domingos, A few useful things to know about machine learning,
Communications of the ACM, Vol. 55 Issue 10, 78-87, October 2012
The most important reading assignment in my Machine Learning
and Data Science and Machine Intelligence Lab at NCTU
52 / 136

The Master Algorithm
53 / 136

The Master Algorithm
54 / 136

Expected Risk vs. Empirical Risk
Assumption: training instances are drawn from an unknown but
ﬁxed probability distribution P(x, y) independently.
Ideally, we would like to have the optimal rule f ∗
that minimizes the
Expected Risk: E(f ) = (f (x), y)dP(x, y) among all functions
Unfortunately, we can not do it. P(x, y) is unknown and we have to
restrict ourselves in a certain hypothesis space, F
How about compute f ∗
∈ F that minimizes the Empirical Risk:
E (f ) = 1
i
(f (xi
), yi )
Only minimizing the empirical risk will be in danger of overﬁtting
55 / 136

Approximation Optimization Approach
Most of learning algorithms can be formulated as an
optimization problem
56 / 136

The objective function consists of two parts: E (f )+ controls
on VC-error bound
57 / 136

on VC-error bound
Controlling the VC-error bound will avoid the overﬁtting risk
58 / 136

on VC-error bound
It can be achieved via adding the regularization term into the
objective function
59 / 136

on VC-error bound
objective function
Note that: We have made lots of approximations when
formulate a learning task as an optimization problem
60 / 136

on VC-error bound
objective function
Note that: We have made lots of approximations when
formulate a learning task as an optimization problem
Why bother to ﬁnd the optimal solution for the problem?
One could stop the optimization iteration before its
convergence
61 / 136

Constrained Optimization Problem
Problem setting: Given function f , gi , i = 1, ..., k and hj ,
j = 1, ..., m, deﬁned on a domain Ω ⊆ Rn,
min
x∈Ω
f (x)
s.t. gi (x) ≤ 0, ∀i
hj (x) = 0, ∀j
where f (x) is called the objective function and g(x) ≤ 0, h(x) = 0
are called constrains.
62 / 136

Example
min f (x) = 2x2
1 + x2
2 + 3x2
3
s.t. 2x1 − 3x2 + 4x3 = 49
<sol>
L(x, β) = f (x) + β(2x1 − 3x2 + 4x3 − 49), β ∈ R
∂
∂x1
L(x, β) = 0 ⇒ 4x1 + 2β = 0
∂
∂x2
L(x, β) = 0 ⇒ 2x2 − 3β = 0
∂
∂x3
L(x, β) = 0 ⇒ 6x3 + 4β = 0
2x1 − 3x2 + 4x3 − 49 = 0 ⇒ β = −6
⇒ x1 = 3, x2 = −9, x3 = 4
63 / 136

x1 + x2 ≤ 4
−x1 − x2 ≤ −2
x1, x2 ≥ 0
f(x) = [2x1, 2x2]
min
x∈R2
x2
1 + x2
2
f(x∗) = [2, 2]
64 / 136

Deﬁnitions and Notation
Feasible region:
F = {x ∈ Ω | g(x) ≤ 0, h(x) = 0}
where g(x) =



g1(x)
...
gk(x)


 and h(x) =



h1(x)
...
hm(x)



A solution of the optimization problem is a point x∗ ∈ F such
that x ∈ F for which f (x) < f (x∗) and x∗ is called a global
minimum.
65 / 136

A point ¯x ∈ F is called a local minimum of the optimization
problem if ∃ε > 0 such that
f (x) ≥ f (¯x), ∀x ∈ F and x − ¯x < ε
At the solution x∗, an inequality constraint gi (x) is said to be
active if gi (x∗) = 0, otherwise it is called an inactive
constraint.
gi (x) ≤ 0 ⇔ gi (x) + ξi = 0, ξi ≥ 0 where ξi is called the slack
variable
66 / 136

Remove an inactive constraint in an optimization problem will
NOT affect the optimal solution
Very useful feature in SVM
If F = Rn then the problem is called unconstrained
minimization problem
Least square problem is in this category
SSVM formulation is in this category
Difficult to find the global minimum without convexity
assumption
67 / 136

The Most Important Concepts in
Optimization(minimization)
A point is said to be an optimal solution of a unconstrained
minimization if there exists no decent direction
=⇒ f (x∗) = 0
A point is said to be an optimal solution of a constrained
minimization if there exists no feasible decent direction
=⇒ KKT conditions
There might exist decent direction but move along this
direction will leave out the feasible region
68 / 136

Minimum Principle
Let f : Rn → R be a convex and diﬀerentiable function F ⊆ Rn be
the feasible region.
x∗
∈ arg min
x∈F
f (x) ⇐⇒ f (x∗
)(x − x∗
) ≥ 0 ∀x ∈ F
Example:
min(x − 1)2
s.t. a ≤ x ≤ b
69 / 136

x1 + x2 ≤ 4
−x1 − x2 ≤ −2
x1, x2 ≥ 0
f(x) = [2x1, 2x2]
min
x∈R2
x2
1 + x2
2
f(x∗) = [2, 2]
70 / 136

Linear Programming Problem
An optimization problem in which the objective function and
all constraints are linear functions is called a linear
programming problem
(LP) min p x
s.t. Ax ≤ b
Cx = d
L ≤ x ≤ U
71 / 136

Linear Programming Solver in MATLAB
X=LINPROG(f,A,b) attempts to solve the linear programming
problem:
min
x
f’*x subject to: A*x <= b
X=LINPROG(f,A,b,Aeq,beq) solves the problem above while
additionally satisfying the equality constraints Aeq*x = beq.
X=LINPROG(f,A,b,Aeq,beq,LB,UB) deﬁnes a set of lower and
upper bounds on the design variables, X, so that the solution
is in the range LB <= X <= UB.
Use empty matrices for LB and UB if no bounds exist. Set
LB(i) = -Inf if X(i) is unbounded below; set UB(i) = Inf if X(i)
is unbounded above.
72 / 136

Linear Programming Solver in MATLAB
X=LINPROG(f,A,b,Aeq,beq,LB,UB,X0) sets the starting point
to X0. This option is only available with the active-set al-
gorithm. The default interior point algorithm will ignore any
non-empty starting point.
You can type “help linprog” in MATLAB to get more information!
73 / 136

L1-Approximation: min
x∈Rn
Ax − b 1
z 1 =
m
i=1
|zi |
min
x,s
1 s
s.t. −s ≤ Ax − b ≤ s
Or
min
x,s
m
i=1
si
s.t. −si ≤ Ai x − bi ≤ si ∀i
min
x,s
0 · · · 0 1 · · · 1
x
s
s.t.
A −I
−A −I 2m×(n+m)
x
s
≤
b
−b
74 / 136

Chebyshev Approximation: min
x∈Rn
Ax − b ∞
z ∞ = max
1≤i≤m
|zi |
min
x,γ
γ
s.t. − 1γ ≤ Ax − b ≤ 1γ
min
x,s
0 · · · 0 1
x
γ
s.t.
A −1
−A −1 2m×(n+1)
x
γ
≤
b
−b
75 / 136

Quadratic Programming Problem
If the objective function is convex quadratic while the
constraints are all linear then the problem is called convex
quadratic programming problem
(QP) min
1
2
x Qx + p x
s.t. Ax ≤ b
Cx = d
L ≤ x ≤ U
76 / 136

Quadratic Programming Solver in MATLAB
X=QUADPROG(H,f,A,b) attempts to solve the quadratic pro-
gramming problem:
min
x
0.5*x’*H*x+f’*x subject to: A*x <= b
X=QUADPROG(H,f,A,b,Aeq,beq) solves the problem
above while additionally satisfying the equality constraints
Aeq*x=beq.
X=QUADPROG(H,f,A,b,Aeq,beq,LB,UB) deﬁnes a set of
lower and upper bounds on the design variables, X, so that
the solution is in the range LB <= X <= UB.
Use empty matrices for LB and UB if no bounds exist. Set
LB(i) = -Inf if X(i) is unbounded below; set UB(i) = Inf if X(i)
is unbounded above.
77 / 136

Quadratic Programming Solver in MATLAB
X=QUADPROG(H,f,A,b,Aeq,beq,LB,UB,X0) sets the starting
point to X0.
You can type “help quadprog” in MATLAB to get more
information!
78 / 136

Standard Support Vector Machine
min
w,b,ξA,ξB
C(1 ξA + 1 ξB) +
1
2
w 2
2
(Aw + 1b) + ξA ≥ 1
(Bw + 1b) − ξB ≤ −1
ξA ≥ 0, ξB ≥ 0
79 / 136

Farkas’ Lemma
For any matrix A ∈ Rm×n and any vector b ∈ Rn, either
Ax ≤ 0, b x > 0 has a solution
or
A α = b, α ≥ 0 has a solution
but never both.
80 / 136

Farkas’ Lemma
Ax ≤ 0, b x > 0 has a solution
b is NOT in the cone generated by A1 and A2
A1
A2
b
Solution Area
{x|b x > 0} ∩ {x|Ax ≤ 0} = 0
81 / 136

Farkas’ Lemma
A α = b, α ≥ 0 has a solution
b is in the cone generated by A1 and A2
A1
A2
b
{x|b > 0} ∩ {x|Ax ≤ 0} = ∅
82 / 136

Minimization Problem
vs.
Kuhn-Tucker Stationary-point Problem
MP:
min
x∈Ω
f (x)
s.t. g(x) ≤ 0
KTSP:
Find ¯x ∈ Ω, ¯α ∈ Rm
such that
f (¯x) + ¯α g(¯x) = 0
¯α g(¯x) = 0
g(¯x) ≤ 0
¯α ≥ 0
83 / 136

Lagrangian Function
L(x, α) = f (x) + α g(x)
Let L(x, α) = f (x) + α g(x) and α ≥ 0
If f (x), g(x) are convex the L(x, α) is convex.
For a ﬁxed α ≥ 0, if ¯x ∈ arg min{L(x, α)|x ∈ Rn}
then
∂L(x, α)
∂x x=¯x
= f (¯x) + α g(¯x) = 0
Above result is a suﬃcient condition if L(x, α) is convex.
84 / 136

KTSP with Equality Constraints?
(Assume h(x) = 0 are linear functions)
h(x) = 0 ⇔ h(x) ≤ 0 and −h(x) ≤ 0
KTSP:
Find ¯x ∈ Ω, ¯α ∈ Rk
, ¯β+, ¯β− ∈ Rm
such that
f (¯x) + ¯α g(¯x) + (¯β+ − ¯β−) h(¯x) = 0
¯α g(¯x) = 0, (¯β+) h(¯x) = 0, (¯β−) (−h(¯x)) = 0
g(¯x) ≤ 0, h(¯x) = 0
¯α ≥ 0, ¯β+, ¯β− ≥ 0
85 / 136

KTSP with Equality Constraints
KTSP:
Find ¯x ∈ Ω, ¯α ∈ Rk
, ¯β ∈ Rm
such that
f (¯x) + ¯α g(¯x) + ¯β h(¯x) = 0
¯α g(¯x) = 0, g(¯x) ≤ 0, h(¯x) = 0
¯α ≥ 0
Let ¯β = ¯β+ − ¯β− and ¯β+, ¯β− ≥ 0
then ¯β is free variable
86 / 136

Generalized Lagrangian Function
L(x, α, β) = f (x) + α g(x) + β h(x)
Let L(x, α, β) = f (x) + α g(x) + β h(x) and α ≥ 0
If f (x), g(x) are convex and h(x) is linear then L(x, α, β) is
convex.
For ﬁxed α ≥ 0, if ¯x ∈ arg min{L(x, α, β)|x ∈ Rn}
then
∂L(x, α, β)
∂x x=¯x
= f (¯x) + α g(¯x) + β h(¯x) = 0
Above result is a suﬃcient condition if L(x, α, β) is convex.
87 / 136

Lagrangian Dual Problem
max
α,β
min
x∈Ω
L(x, α, β)
s.t. α ≥ 0
88 / 136

Lagrangian Dual Problem
max
α,β
min
x∈Ω
L(x, α, β)
s.t. α ≥ 0
max
α,β
θ(α, β)
s.t. α ≥ 0
where θ(α, β) = inf
x∈Ω
L(x, α, β)
89 / 136

Weak Duality Theorem
Let ¯x ∈ Ω be a feasible solution of the primal problem and (α, β) a
feasible sulution of the dual problem. then f (¯x) ≥ θ(α, β)
θ(α, β) = inf
x∈Ω
L(x, α, β) ≤ L(˜x, α, β)
Corollary:
sup{θ(α, β)|α ≥ 0} ≤ inf{f (x)|g(x) ≤ 0, h(x) = 0}
90 / 136

Weak Duality Theorem
Corollary
If f (x∗) = θ(α∗, β∗) where α∗ ≥ 0 and g(x∗) ≤ 0 , h(x∗) = 0
,then x∗ and (α∗, β∗) solve the primal and dual problem
respectively. In this case,
0 ≤ α ⊥ g(x) ≤ 0
91 / 136

Saddle Point of Lagrangian
Let x∗ ∈ Ω,α∗ ≥ 0, β∗ ∈ Rm satisfying
L(x∗
, α, β) ≤ L(x∗
, α∗
, β∗
) ≤ L(x, α∗
, β∗
) , ∀x ∈ Ω , α ≥ 0
Then (x∗, α∗, β∗) is called The saddle point of the Lagrangian
function
92 / 136

Saddle Point of f (x, y) = x2
− y2
Saddle point of
22
),( yxyxf −=
93 / 136

Dual Problem of Linear Program
Primal LP min
x∈Rn
p x
subject to Ax ≥ b , x ≥ 0
Dual LP max
α∈Rm
b α
subject to A α ≤ p , α ≥ 0
All duality theorems hold and work perfectly!
94 / 136

Lagrangian Function of Primal LP
L(x, α) = p x + α1 (b − Ax) + α2 (−x)
max
α1,α2≥0
min
x∈Rn
L(x, α1, α2)
max
α1,α2≥0
p x + α1 (b − Ax) + α2 (−x)
subject to p − A α1 − α2 = 0
( x L(x, α1, α2) = 0)
95 / 136

Application of LP Duality
LSQ − NormalEquation Always Has a Solution
For any matrix A ∈ Rmxn and any vector b ∈ Rm ,
consider min
x∈Rn
Ax − b 2
2
x∗
∈ arg min{ Ax − b 2
2} ⇔ A Ax∗
= A b
Claim : A Ax = A b always has a solution.
96 / 136

Dual Problem of Strictly Convex Quadratic Program
Primal QP
min
x∈Rn
1
2
x Qx + p x
s.t. Ax ≤ b
With strictlyconvex assumption, we have
Dual QP
max −
1
2
(p + α A)Q−1
(A α + p) − α b
s.t. α ≥ 0
97 / 136

Outline
Some Examples
3 Optimization
98 / 136

Linearly Separable Case
x w + b = 0
x w + b = −1
x w + b = +1
A-
Malignant
A+
Benign
w
99 / 136

Support Vector Machines
Maximizing the Margin between Bounding Planes
x w + b = −1
x w + b = +1
A-
A+
w
2
w 2
= Margin
100 / 136

Why Use Support Vector Machines?
Powerful tools for Data Mining
SVM classifier is an optimally defined surface
SVMs have a good geometric interpretation
SVMs can be generated very efficiently
Can be extended from linear to nonlinear case
Typically nonlinear in the input space
Linear in a higher dimensional ”feature space”
Implicitly defined by a kernel function
Have a sound theoretical foundation
Based on Statistical Learning Theory
101 / 136

Why We Maximize the Margin?
(Based on Statistical Learning Theory)
The Structural Risk Minimization (SRM):
The expected risk will be less than or equal to empirical risk
(training error)+ VC (error) bound
w 2 ∝ VC bound
min VC bound⇔ min 1
2 w 2
2 ⇔ max Margin
102 / 136

Summary the Notations
Let S = {(x1, y1), (x2, y2), . . . , (x , y ) be a training dataset and
represented by matrices
A =





(x1)
(x2)
...
(x )





∈ R ×n
, D =



y1 · · · 0
...
...
...
0 · · · y


 ∈ R ×
Ai w + b ≥ +1, for Dii = +1
Ai w + b ≤ −1, for Dii = −1 , equivalent to D(Aw + 1b) ≥ 1 ,
where 1 = [1, 1, . . . , 1] ∈ R
103 / 136

Support Vector Classiﬁcation
(Linearly Separable Case, Primal)
The hyperplane (w, b) is determined by solving the minimization
problem:
min
(w,b)∈Rn+1
1
2
w 2
2
D(Aw + 1b) ≥ 1,
It realizes the maximal margin hyperplane with geometric margin
γ =
1
w 2
104 / 136

Support Vector Classiﬁcation
(Linearly Separable Case, Dual Form)
The dual problem of previous MP:
max
α∈R
1 α −
1
2
α DAA Dα
subject to
1 Dα = 0, α ≥ 0
Applying the KKT optimality conditions, we have w = A Dα. But
where is b ?
Don’t forget
0 ≤ α ⊥ D(Aw + 1b) − 1 ≥ 0
105 / 136

Dual Representation of SVM
(Key of Kernel Methods: w = A Dα∗
=
i=1
yiα∗
i Ai )
The hypothesis is determined by (α∗, b∗)
h(x) = sgn( x · A Dα∗
+ b∗
)
= sgn(
i=1
yi α∗
i xi
· x + b∗
)
= sgn(
α∗
i >0
yi α∗
i xi
· x + b∗
)
Remember : Ai = xi
106 / 136

Soft Margin SVM
(Nonseparable Case)
If data are not linearly separable
Primal problem is infeasible
Dual problem is unbounded above
Introduce the slack variable for each training point
yi (w xi
+ b) ≥ 1 − ξi , ξi ≥ 0, ∀i
The inequality system is always feasible e.g.
w = 0, b = 0, ξ = 1
107 / 136

x w + b = −1
x w + b = +1
A-
A+
w
ξi
ξj
2
w 2
= Margin
108 / 136

Robust Linear Programming
Preliminary Approach to SVM
min
w,b,ξ
1 ξ
s.t. D(Aw + 1b) + ξ ≥ 1 (LP)
ξ ≥ 0
where ξ is nonnegative slack(error) vector
The term 1 ξ, 1-norm measure of error vector, is called the
training error
For the linearly separable case, at solution of(LP): ξ = 0
109 / 136

Support Vector Machine Formulations
(Two Diﬀerent Measures of Training Error)
2-Norm Soft Margin:
min
(w,b,ξ)∈Rn+1+
1
2
w 2
2 +
C
2
ξ 2
2
D(Aw + 1b) + ξ ≥ 1
1-Norm Soft Margin (Conventional SVM)
min
(w,b,ξ)∈Rn+1+
1
2
w 2
2 + C1 ξ
D(Aw + 1b) + ξ ≥ 1
ξ ≥ 0
110 / 136

Tuning Procedure
How to determine C ?Tuning Procedure
How to determine C?
overfitting
The final value of parameter is one with
the maximum testing set correctness !
C
The ﬁnal value of parameter is one with the maximum testing set
correctness!
111 / 136

1-Norm SVM
(Diﬀerent Measure of Margin)
1-Norm SVM:
min
(w,b,ξ)∈Rn+1+
w 1 +C1 ξ
D(Aw + 1b) + ξ ≥ 1
ξ ≥ 0
Equivalent to:
min
(s,w,b,ξ)∈R2n+1+
1s + C1 ξ
D(Aw + 1b) + ξ ≥ 1
−s ≤ w ≤ s
ξ ≥ 0
Good for feature selection and similar to the LASSO
112 / 136

Two-spiral Dataset
(94 white Dots & 94 Red Dots)
Two-spiral Dataset
(94 White Dots & 94 Red Dots)
113 / 136

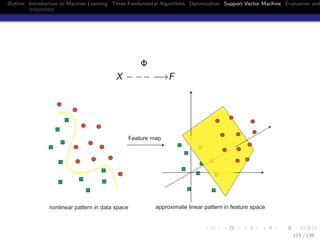
Learning in Feature Space
(Could Simplify the Classiﬁcation Task)
Learning in a high dimensional space could degrade
generalization performance
This phenomenon is called curse of dimensionality
By using a kernel function, that represents the inner product
of training example in feature space, we never need to
explicitly know the nonlinear map
Even do not know the dimensionality of feature space
There is no free lunch
Deal with a huge and dense kernel matrix
Reduced kernel can avoid this diﬃculty
114 / 136

Φ
X − −− −→F
Feature map
nonlinear pattern in data space approximate linear pattern in feature space
115 / 136

Linear Machine in Feature Space
Let φ : X −→ F be a nonlinear map from the input space to some
feature space
The classiﬁer will be in the form(primal):
f (x) = (
?
j=1
wj φj (x)) + b
Make it in the dual form:
f (x) = (
i=1
αi yi φ(xi
) · φ(x) ) + b
116 / 136

Kernel:Represent Inner Product
in Feature Space
Deﬁnition: A kernel is a function K : X × X −→ R
such that for all x, z ∈ X
K(x, z) = φ(x) · φ(z)
where φ : X −→ F
The classiﬁer will become:
f (x) = (
i=1
αi yi K(xi
, x)) + b
117 / 136

A Simple Example of Kernel
Polynomial Kernel of Degree 2: K(x,z)= x, z 2
Let x =
x1
x2
, z =
z1
z2
∈ R2 and the nonlinear map
φ : R2 −→ R3 deﬁned by φ(x) =


x2
1
x2
2√
2x1x2

.
Then φ(x), φ(z) = x, z 2 = K(x, z)
There are many other nonlinear maps, ψ(x), that satisfy the
relation: ψ(x), ψ(z) = x, z 2 = K(x, z)
118 / 136

Power of the Kernel Technique
Consider a nonlinear map φ : Rn −→ Rp that consists of distinct
features of all the monomials of degree d.
Then p =
n + d − 1
d
.
x3
1 x1
2 x4
3 x4
4 =⇒ x o o o x o x o o o o x o o o o
For example: n=11, d=10, p=92378
Is it necessary? We only need to know φ(x), φ(z) !
This can be achieved K(x, z) = x, z d
119 / 136

Kernel Technique
Based on Mercer’s Condition(1909)
The value of kernel function represents the inner product of
two training points in feature space
Kernel function merge two steps
1 map input data from input space to feature space (might be
inﬁnite dim.)
2 do inner product in the feature space
120 / 136

Example of Kernel
K(A, B) : R ×n
× Rn×˜
−→ R ×˜
A ∈ R ×n, a ∈ R , µ ∈ R, d is an integer:
Polynomial Kernel:
(AA + µaa )d
• (Linear KernelAA : µ = 0, d = 1)
Gaussian (Radial Basis) Kernel:
K(A, A )ij = e−µ Ai −Aj
2
2 , i, j = 1, ..., m
The ij-entry of K(A, A ) represents the ”similarity” of data
points Ai and Aj
121 / 136

Nonlinear Support Vector Machine
(Applying the Kernel Trick)
1-Norm Soft Margin Linear SVM:
max
α∈R
1 α −
1
2
α DAA Dα s.t. 1 Dα = 0, 0 ≤ α ≤ C1
Applying the kernel trick and running linear SVM in the
feature space without knowing the nonlinear mapping
1-Norm Soft Margin Nonlinear SVM:
max
α∈R
1 α −
1
2
α DK(A, A )Dα
s.t. 1 Dα = 0, 0 ≤ α ≤ C1
All you need to do is replacing AA by K(A, A )
122 / 136

1-Norm SVM
(Diﬀerent Measure of Margin)
1-Norm SVM:
min
(w,b,ξ)∈Rn+1+
w 1 +C1 ξ
D(Aw + 1b) + ξ ≥ 1
ξ ≥ 0
Equivalent to:
min
(s,w,b,ξ)∈R2n+1+
1s + C1 ξ
D(Aw + 1b) + ξ ≥ 1
−s ≤ w ≤ s
ξ ≥ 0
Good for feature selection and similar to the LASSO
123 / 136

Outline
Some Examples
3 Optimization
124 / 136

How to Evaluated What’s been learned
Cost is not sensitive
Measure the performance of a classifier in terms of error rate
or accuracy
Error rate =
Number of misclassified point
Total number of data point
Main Goal: Predict the unseen class label for new data
We have to asses a classifier’s error rate on a set that play no
rule in the learning class
Split the data instances in hand into two parts:
1 Training set: for learning the classifier.
2 Testing set: for evaluating the classifier.
125 / 136

k-fold Stratified Cross Validation
Maximize the usage of the data in hands
Split the data into k approximately equal partitions.
Each in turn is used for testing while the remainder is used for
training.
The labels (+/−) in the training and testing sets should be in
about right proportion.
Doing the random splitting in the positive class and negative
class respectively will guarantee it.
This procedure is called stratification.
Leave-one-out cross-validation if k = # of data point.
No random sampling is involved but nonstratified.
126 / 136

How to Compare Two Classiﬁer?
Testing Hypothesis:Paired t-test
We compare two leaving algorithm by comparing the average
error rate over several cross-validations.
Assume the same cross-validation split can be used for both
methods
H0 : ¯d = 0 v.s H1 : ¯d = 0
where ¯d = 1
k
k
i=1 di and di = xi − yi
The t-statistic:
t =
¯d
σ2
d /k
127 / 136

How to Evaluate What’s Been Learned?
When cost is sensitive
Two types error will occur: False Positive(FP) & False
Negative(FN)
For binary classiﬁcation problem, the results can be
summarized in a 2 × 2 confusion matrix.
Predicted Class
True Pos.
(TP)
False Neg.
(FN)
Actual
Class
False Pos.
(FP)
True Neg.
(FN)
128 / 136

ROC Curve
Receiver Operating Characteristic Curve
An evaluation method for learning models.
What it concerns about is the Ranking of instances made by
the learning model.
A Ranking means that we sort the instances w.r.t the
probability of being a positive instance from high to low.
ROC curve plots the true positive rate (TPr) as a function of
the false positive rate (FPr).
129 / 136

An example of ROC Curve
130 / 136

Using ROC to Compare Two Methods
Figure: Under the same FP rate, method A is better than B.
131 / 136

Using ROC to Compare Two Methods
132 / 136

Area under the Curve (AUC)
An index of ROC curve with range from 0 to 1.
An AUC value of 1 corresponds to a perfect Ranking (all
positive instances are ranked high than all negative instance).
A simple formula for calculating AUC:
AUC =
m
i=1
n
j=1 If (xi )>f (xj )
m
where m: number of positive instances.
n: number of negative instances.
133 / 136

Performance Measures in Information Retrieval (IR)
An IR system, such as Google, for given a query (keywords
search) will try to retrieve all relevant documents in a corpus.
Documents returned that are NOT relevant: FP.
The relevant documents that are NOT return: FN.
Performance measures in IR, Recall & Precision.
Recall =
TP
TP + FN
and
Precision =
TP
TP + FP
134 / 136

Balance the Trade-off between Recall and Precision
Two extreme cases:
1 Return only document with 100% confidence then precision=1
but recall will be very small.
2 Return all documents in the corpus then recall=1 but precision
will be very small.
F-measure balances this trade-off:
F − measure =
2
1
Recall
+
1
Precision
135 / 136

Reference
C. J. C Burges. ”A Tutorial on Support Vector Machines for
Pattern Recognition”, Data Mining and Knowledge Discovery,
Vol. 2, No. 2, (1998) 121-167.
N. Cristianini and J. Shawe-Taylor. ”An Introduction to
Support Vector Machines”, Cambridge University Press,(2000).
136 / 136

[系列活動] Machine Learning 機器學習課程

Recommended

More Related Content

What's hot (20)

Viewers also liked (20)

Similar to [系列活動] Machine Learning 機器學習課程 (20)

More from 台灣資料科學年會 (20)

Recently uploaded (20)

[系列活動] Machine Learning 機器學習課程