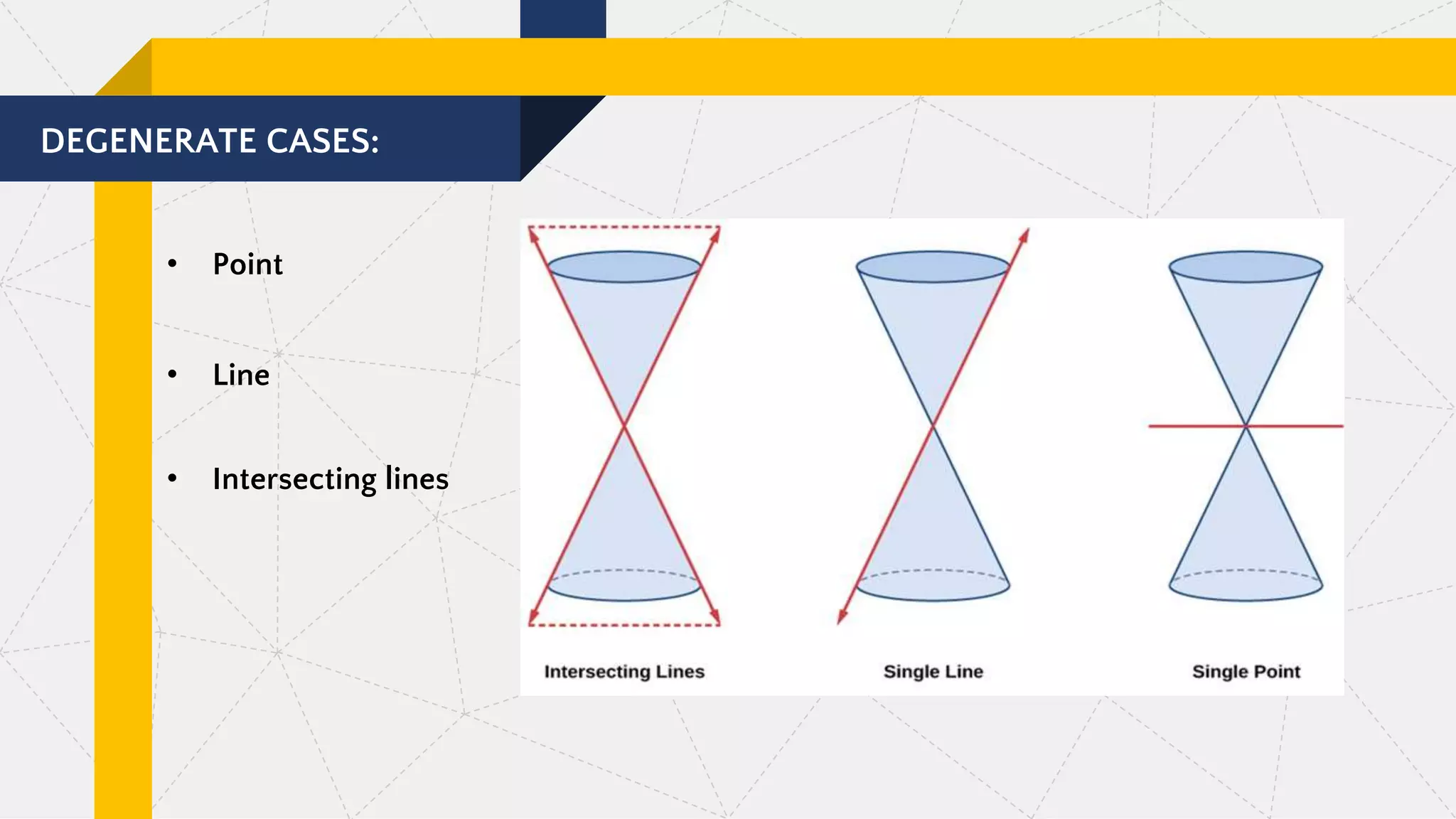
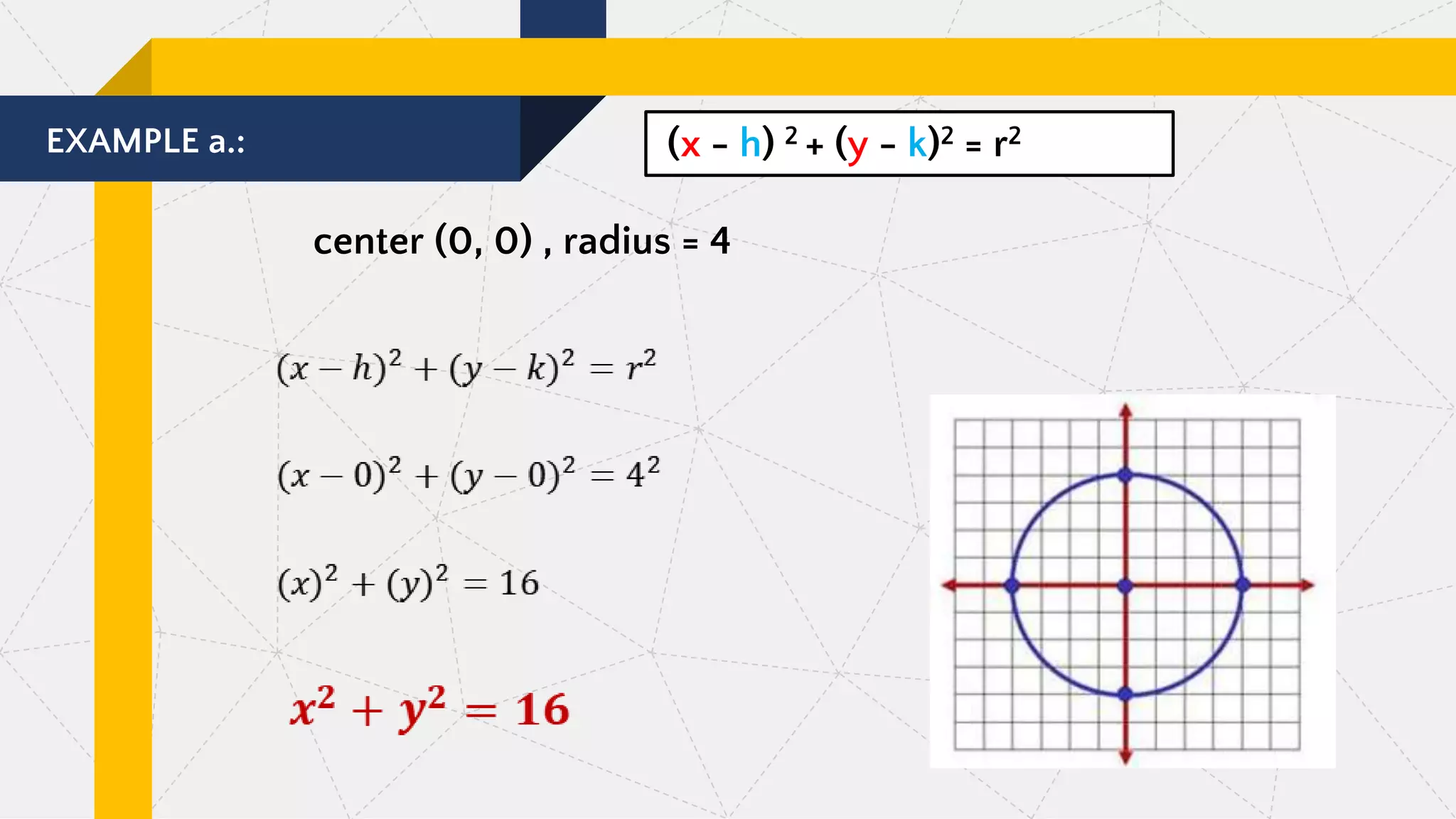
This document discusses pre-calculus concepts related to conic sections including circles. It defines conic sections as curves formed by the intersection of a plane and a double right circular cone. The main types of conic sections are defined as circles, ellipses, parabolas, and hyperbolas. Circles are defined as sets of points equidistant from a fixed center point, and the standard form of a circle equation is given as (x - h)2 + (y - k)2 = r2, where (h, k) is the center and r is the radius. Several examples are provided of writing the standard form of circle equations given the center and radius.