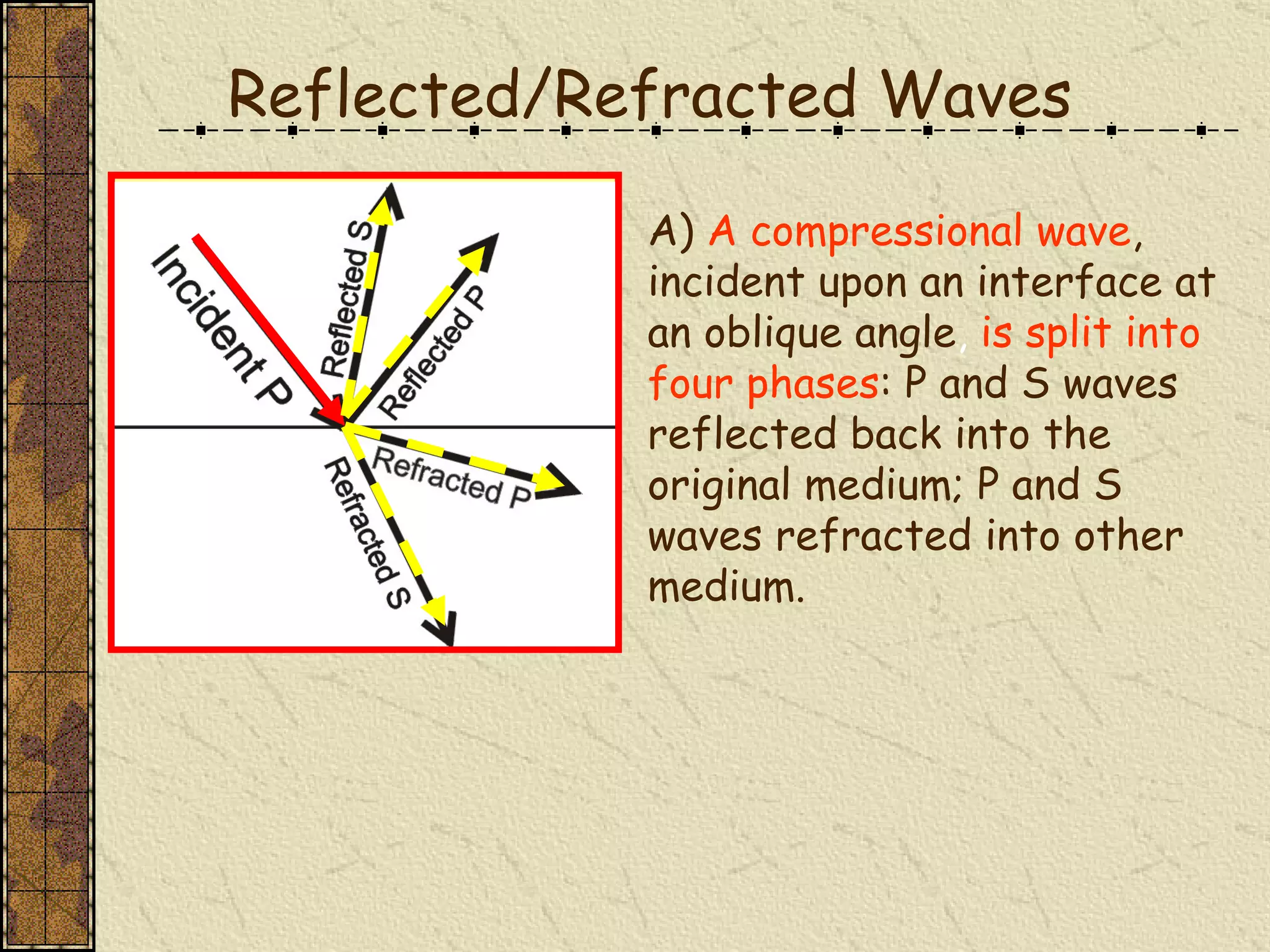
The document discusses seismic wave velocity and how it relates to rock properties. It covers topics like:
- P-wave and S-wave velocity are inversely proportional to the square root of density based on Nafe-Drake curves.
- Seismic velocity in a homogeneous medium can be calculated using the appropriate elastic modulus divided by density.
- Factors like lithology, porosity, fluids, and compaction influence rock seismic velocities.
- Huygen's and Fermat's principles describe how seismic waves propagate through materials with different velocities.
![Introduction to Geophysics Ali Oncel [email_address] Department of Earth Sciences KFUPM Seismic Exploration: Fundamentals 1](https://image.slidesharecdn.com/lecture3-1-091220221338-phpapp02/75/ONCEL-AKADEMI-INTRODUCTION-TO-GEOPHYSICS-1-2048.jpg)