Stack data structure

IMPLEMENTATION OF STACKS
PART 1

INTRODUCTION ABOUT STACKS
The stack is a very common data structure used in programs which has
lot of potential.
 Stacks hold objects, usually all of the same type.
 It follows the concept of LIFO – last in first out.
 Stack is a linear list of items in which all additions and deletion are
restricted to one end.
 Some languages, like LISP and Python, do not call for stack
implementations, since push and pop functions are available for any list.
 All Forth-like languages (such as Adobe PhotoScript) are also designed
around language-defined stacks that are directly visible to and
manipulated by the programmer.

STACKS VS ARRAYS
 An array is a contiguous block of memory.
 A stack is a first-in-last-out data structure with access only to the top
of the data.
 Since many languages does not provide facility for stack, it is backed
by either arrays or linked list.
 The values can be added and deleted on any side from an array.
 But in stack, insertion and deletion is possible on only one side of the
stack. The other side is sealed.
Eg: a[10] –array a[10] - stack

STACK OPERATIONS
The bottom of a stack is a sealed end. Stack may have a capacity
which is a limitation on the number of elements in a stack. The operations
on stack are
•Push: Places an object on the top of the stack.
• Pop: Removes an object from the top of the stack.
• IsEmpty: Reports whether the stack is empty or not.
• IsFull: Reports whether the stack exceeds limit or not.
c
b
a a
(i)stack (ii)push(s,a) (iii)push(s,d)-stack overflow (iv)pop(s)

(v)pop(s)-stack underflow

STACK OPERATIONS

B
E
D
A
A B C D E

STACK IMPLEMENTATION
 Stack data structure is not inherently provided by many programming
languages.
 Stack is implemented using arrays or linked lists.
 Let S be a stack, n be the capacity, x be the element to be pushed, then
push and pop will be given as
Push(S,x) and Pop(S)
 Here we use “top” which keeps track of the top element in the stack.
 When top = = 0 , and pop() operation gives stack underflow as result.
 When top = = n, and push() operation gives stack overflow as result.
 The pop() operation just gives an illusion of deletion, but the elements
are retained. Only the top is decremented.

S[1:6] Pop(S) a b c d
e Top=5

Push(S,a) a Pop(S) a
Pop(S) Top=1
Top=1 Pop(S)
Pop(S) pop(S)
Push(S,a) a b c d e f
Push(S,b)
Push(S,c) push(S,d) Top=6 Pop(S)
Push(S,e) push(S,f) Top=0

Push(S,g) a b c d e f Pop(S)
Top=6 = n Top=0 stack underflow
Stack overflow

STACK APPLICATIONS
 Recursion handling
 Evaluation of expression
Conversion of infix to postfix expression
Computation of postfix expression
 Parenthesis handling
 Backtracking
Conversion of decimal to other number system
Maze tracer
Undo operations

RECURSION HANDLING
 Without stack, recursion is difficult
 Compiler automatically uses stack data structure while handling
recursion.
 All computer needs to remember for each active function call, values
of arguments & local variables and the location of the next statement
to be executed when control goes back.
 Essentially what is happening when we call that method is that our
current execution point is pushed onto the call stack and the runtime
starts executing the code for the internal method call. When that
method finally returns, we pop our place from the stack and continue
executing.

Eg: int f(int n)
{ int k,r;
if(n==0) return 0;
k=n*n;
r=f(n-1);
Return k+r;
}

n 3 3 3 2 3 2 1
- 9 9 4 9 4 1
k
r - . . . . . .

n 3 2 1 3 2 3
9 4 1 9 4 9
k
r . . 0 . 1 5

Ans: 14

PARENTHESIS CHECKING
Procedure check()
Declare a character stack S.
Now traverse the expression.
a) If the current character is a starting bracket then push it to
stack.
b) If the current character is a closing bracket then pop from
stack and if the popped character is the matching starting bracket
then fine else parenthesis are not balanced.
After complete traversal, if there is some starting bracket left in stack
then “not balanced”
End procedure

Eg: [a+(b*c)+{(d-e)}]

[ Push [

[ ( Push (

[ ) and ( matches, Pop (

[ { Push {

[ { ( Push (

matches, pop (
[ {

[ Matches, pop {

Matches, pop [

Thus, parenthesis match here

CONVERSION OF INFIX TO POSTFIX
 Expressions can be represented in prefix, postfix or infix notations.
 Conversion from one form of the expression to another form may be
accomplished using a stack.
We do not know what to do if an operator is read as an input character.
By implementing the priority rule for operators, we have a solution to this
problem.
The Priority rule: we should perform comparative priority check if an
operator is read, and then push it. If the stack top contains an operator of
priority higher than or equal to the priority of the input operator, then we
pop it and print it. We keep on performing the priority check until the top
of stack either contains an operator of lower priority or if it does not
contain an operator.

Eg: (A*B)+C

Element Stack Prefix Action

$ $ Work stack

( $ ( Push (

A $ ( A Print A

* $ ( * Push(*)

B $ ( * AB Print B

) $ AB* Pop *,( print *

+ $ + Push +

C $ + AB*C Print C

$ AB*C+ Pop +

EVALUATION OF POSTFIX EXPRESSION
 Postfix expression is easily evaluated by the compiler by using stack.
 The procedure for the evaluation of postfix expression is given below:
procedure eval(E)
x=getnextchar(E);
case x:
x is an operand: push x into stack S.
x is an operator: pop elements, perform operation and
push result into stack.
x is null: pop stack and print result
end case
End procedure

Eg: AB*C+ A=2, B=3, C=5

Element Stack Action
A Push A
A
B Push B
A B
* 6 Pop A and B, A*B,
push 6

C 6 C Push C

+ 11 Pop C and 6,
C+6, push 11
$
Pop

Result:11

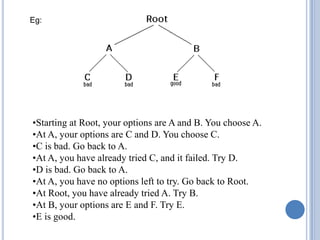
BACKTRACKING
Backtracking is a simple, elegant, recursive technique which can be put to a
variety of uses.
 You start at the root of a tree, the tree probably has some good and bad
leaves. You want to get to a good leaf. At each node, you choose one of its
children to move to, and you keep this up in a stack until you get to a leaf.
 Suppose you get to a bad leaf. You can backtrack to continue the search for
a good leaf by revoking your most recent choice, and trying out the next
option in that set of options.
 If you run out of options, revoke the choice that got you here, and try
another choice at that node.
 If you end up at the root with no options left, there are no good leaves to be
found.

Eg:

•Starting at Root, your options are A and B. You choose A.
•At A, your options are C and D. You choose C.
•C is bad. Go back to A.
•At A, you have already tried C, and it failed. Try D.
•D is bad. Go back to A.
•At A, you have no options left to try. Go back to Root.
•At Root, you have already tried A. Try B.
•At B, your options are E and F. Try E.
•E is good.

CONVERSION OF DECIMAL TO OTHER NUMBER SYSTEM

The given decimal number is divided by the base (2 or 8 or 16)
repeatedly and the corresponding remainders are pushed into stack.
At last the elements are popped out of the stack to give the result.

Eg. 84 – 1010100 in binary
124 in octal
54 in hexadecimal

84 / 2 = 42 0 1
42 / 2 = 21 0 pop 1010100
0
21 / 2 = 10 1
10 / 2 = 5 0 1
5/2=2 1 0
2/2=1 0
1
1
0
push 0

84 / 8 = 10 4
10 / 8 = 1 2 1 pop 124
1 2
push 4

84 / 16 = 5 4
5 5
push pop 54
4

MAZE TRACER
All our mazes will be two-dimensional arrays of n rows and n
columns. Each row, column cell is either open, or blocked by an internal
wall. From any open cell, you may move left, right, up, or down to an
adjacent empty cell. To solve a maze, you must find a path of open cells
from a given start cell to a specified end cell. By default, you should
assume that the start cell is in position (0,0).
Sample:
SOOOOO
HHHHOH
HOOOOH
HOHHHH
HOHOOO
HOOOHE

The path will be: [(0,0),(0,1),(0,2),(0,3),(0,4), (1,4),(2,4),(2,3), (2,2),(2,1),(3,1),
(4,1),(5,1),(5,2),(5,3),(4,3),(4,4), (4,5),(5,5)]

SOOOOO
HHHHOH
HOOOOH
HOHHHH
HOHOOO
HOOOHE

2 4
0 5 1 4 1 4
0 4 0 4 0 4 0 4
0 0 0 3 0 3 0 3 0 3
Push start (0,0) 0 2 0 2 0 2 0 2
0 1 0 1 0 1 0 1

0 0 0 0 0 0 0 0
Push Pop Push Push

4 1 5 5 End
2 1 4 5
3 1 4 4 4 5
2 2 2 1 4 4
4 3
2 3 4 3
2 2 5 3
2 4 5 3
2 3 5 2
1 4 5 2
2 4 5 1
0 4 1 4 5 1
4 1
0 3 0 4 3 1 4 1
0 2 2 1 3 1
0 3
0 1 2 1
0 2 2 2
2 3 2 2
0 0 0 1
2 4 2 3
Push
0 0 1 4 2 4
Push 1 4
0 4
0 4
0 3
0 2 0 3
0 2
0 1
0 1
0 0
start 0 0
Push
Push

UNDO OPERATION
 An undo operation is a method for reverting a change to an object,
along with the arguments needed to revert the change.
Undo operations are typically collected in undo groups, which
represent whole revertible actions, and are stored on a stack.
 To undo a single operation, it must still be packaged in a group.
 Undo groups are stored on a stack, with the oldest groups at the
bottom and the newest at the top.
 The undo stack is unlimited by default, but you can restrict it.
 When the stack exceeds the maximum, the oldest undo groups are
dropped from the bottom.

UNDO OPERATION
Initially, both stacks are empty. Recording undo operations adds to the
undo stack, but the redo stack remains empty until undo is performed.
 Performing undo causes the reverting operations in the latest group to
be applied to their objects.
Consecutive undos add to the redo stack. Subsequent redo operations
pull the operations off the redo stack, apply them to the objects, and
push them back onto the undo stack.
The redo stack’s contents last as long as undo and redo are performed
successively. However, because applying a new change to an object
invalidates the previous changes, as soon as a new undo operation is
registered, any existing redo stack is cleared.

Stack data structure

More Related Content

What's hot (20)

Viewers also liked (9)

Similar to Stack data structure (20)

More from Tech_MX (20)

Recently uploaded (20)

Stack data structure