The document provides information about electronic spectra and terms for carbon p electrons and transition metal d electron configurations. It discusses:
1) Possible terms that arise from carbon's 2p electrons, including 1D2, 3P2, 3P1, 3P0 and 1S0 terms. Hund's rules are used to determine the ground state term.
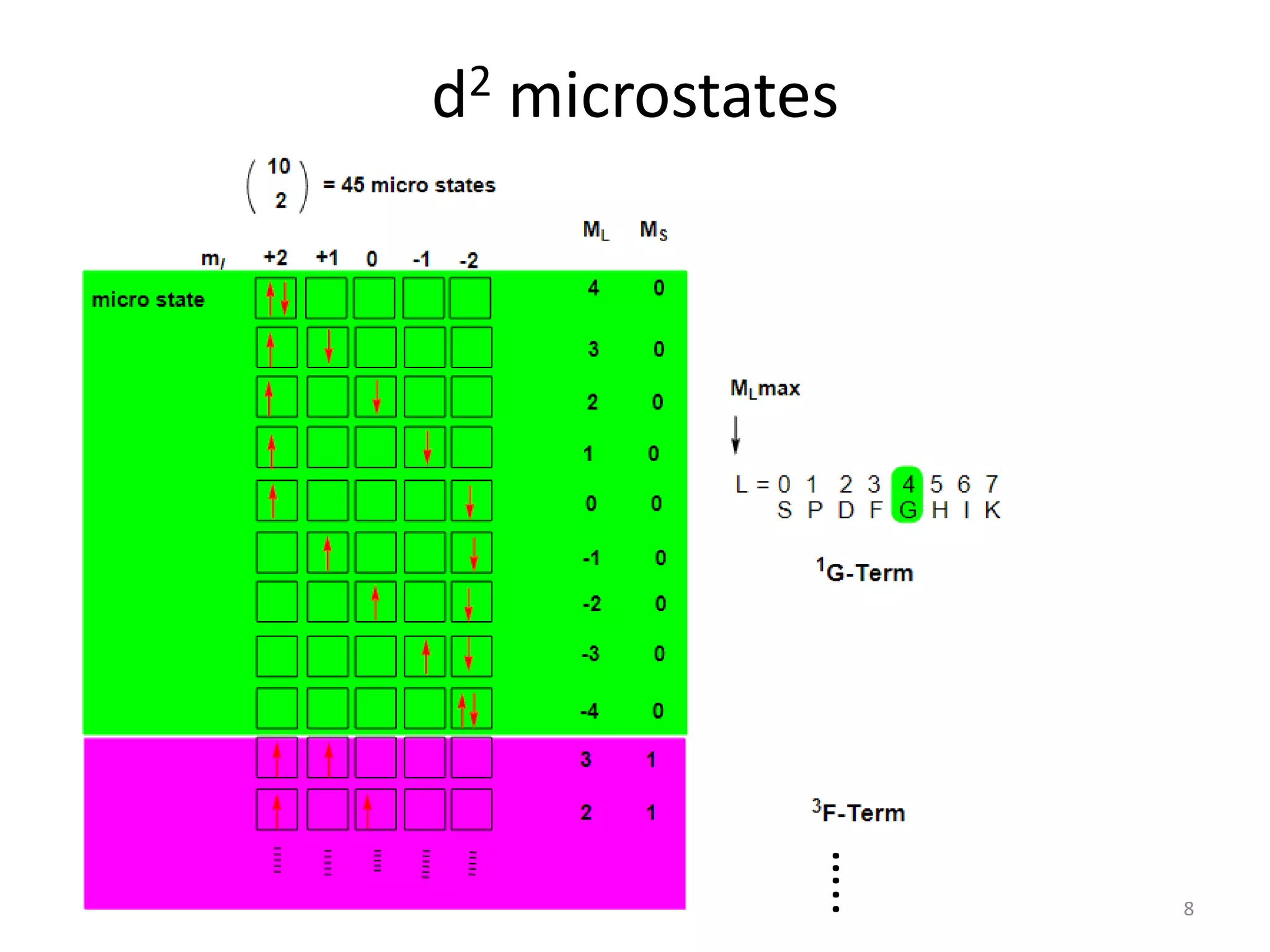
2) Microstate tables that list all possible combinations of orbital angular momentum (L) and spin (S) for electron configurations.
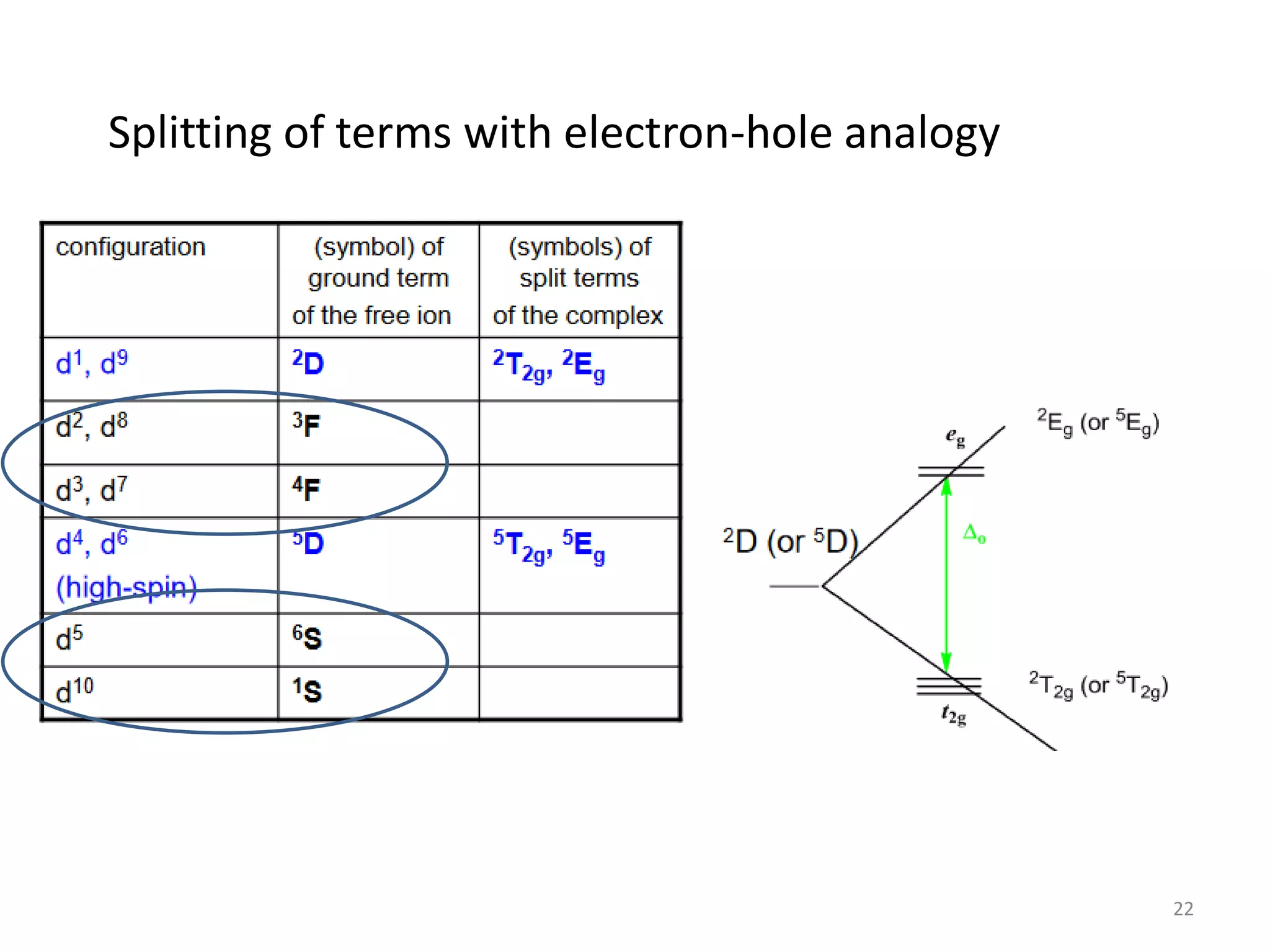
3) Tanabe-Sugano diagrams that show the splitting of d electron terms in an octahedral ligand field and allow determination of transition energies.
4) Charge transfer transitions that can occur from the













































![d3 case
4T2g <--- 4A2g
4T1g <--- 4A2g
4T1g(P) <--- 4A2g
Calculate the value of B and Δ for the Cr3+ ion in [Cr(H2O)6)]3+ if
1=17000 cm-1, 2=24000 cm-1 and 3=37000 cm-1.
SOLUTION.
These values have been assigned to the following spin-allowed
transitions.
From the information given, the ratio 2 / 1 = 24000 / 17000 = 1.412
Using a Tanabe-Sugano diagram for a d3 system this ratio is found at
Δ/B=24.0
48](https://image.slidesharecdn.com/lecture2019exercises-190320122205/75/Transition-Metal-Electronic-Spectra-48-2048.jpg)




